本文来自微信公众号:瞻云(ID:zhanyun2028),作者:瞻云,题图来自:视觉中国
太阳对月球的引力是地球2.2倍,为啥月亮没被太阳抢走?而且,月球中心天体也不是太阳,为啥反而是地球?
其实,月球中心天体不是太阳,与月球绕着太阳转并不矛盾。
通过万有引力公式:
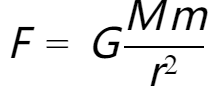
我们很容易求得,太阳对月球的引力,是地球对月球的引力的2.2倍。
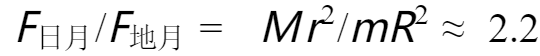
M为太阳质量:1.989×1030kg。m为地球质量:5.965×1024kg。r为月地距离(均值):384403.9km。R为日月距离(均值):149597870km。
既然,太阳对月亮的引力,是地球对月亮的引力的2.2倍。
为什么月球的中心天体是地球,而不是太阳?

首先,在整个地月系统中,太阳对月球轨道的影响十分有限。
月初时,月球运动到靠近太阳的一面,日月距离约为:R朔=149597870−384403.9=149213466.1km。
月中时,月球运动到远离太阳的一面,日月距离约为:R望=149597870+384403.9=149982273.9km。
月球朔望日的引力差,与地日引力比值为:
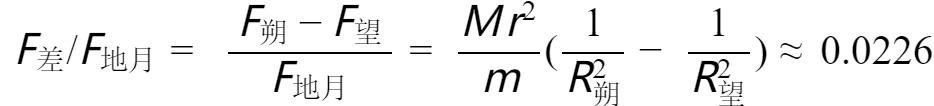
也就是说,相对于日地距离,月球围绕地球的轨道变化十分微小。
当月球围绕地球进行圆周运动时,因为太阳引力而产生的引力差,只有月球受到地球引力的2.3%左右。
因此,太阳引力对月球轨道的引力波动,只会有很小的影响。
在地月系中,月球轨道依旧由地球引力所主导,甚至被地球潮汐锁定。
行星/卫星与中心天体的轨道关系,符合开普勒三大定律。
开普勒三大定律可以简略地用于地月系统。
当然,如果不考虑太阳引力,是无法求出月球精准轨道的。
其次,如果把日月看作一个独立系统,地球对日月系统的影响十分巨大。
日地引力达到日月引力的45%,如果要排除地球,仅仅考虑日月关系来求取月亮相对于太阳的轨道,将完全无法适用于开普勒三大定律。
实际上由于月球被地球潮汐锁定,月球绕太阳的椭圆轨道,大尺度上反而十分的接近日地轨道。
因此,按照中心天体的典型定义,地球为月球的中心天体,而不是太阳。
不过太阳却是地球的中心天体。
本质上,日地月可以看作以太阳为主导的三星系统。
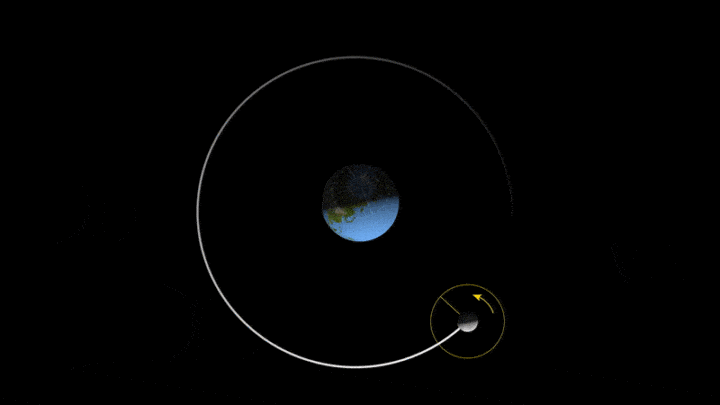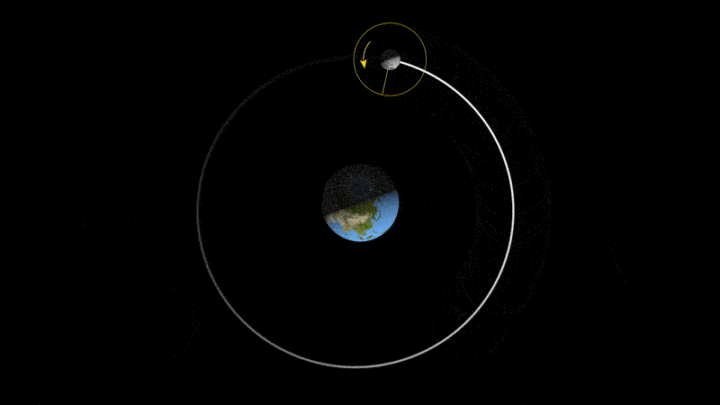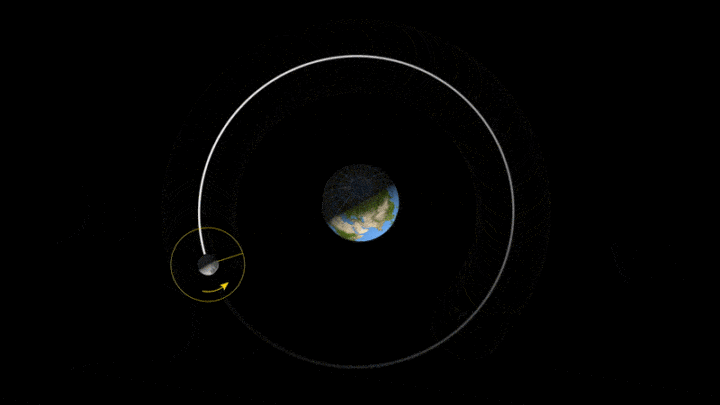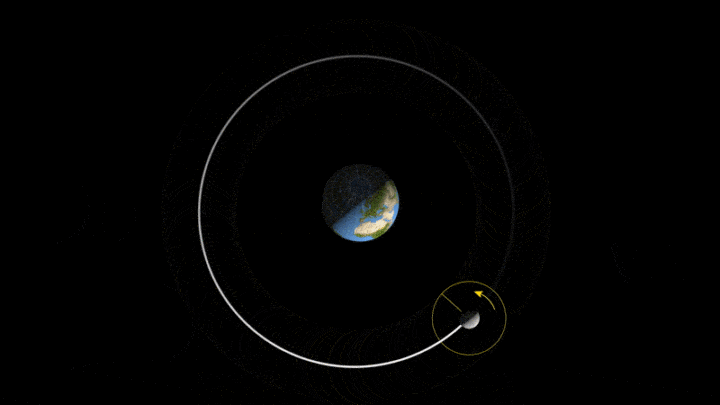
地月系统作为整体围绕着太阳旋转,月球自然也围绕太阳进行非典型的旋转。
由于地月系统绕着太阳运动的速度是29.78km/s,而月球绕着地球运动的速度是1.023km/s。前者速度大于后者,所以,日地月系统的轨道,接近于这样的状态:
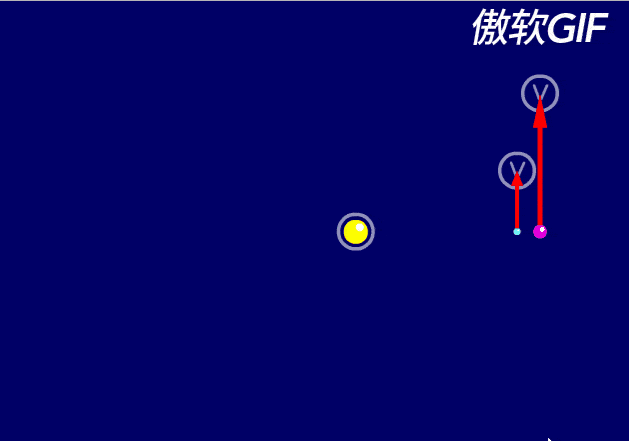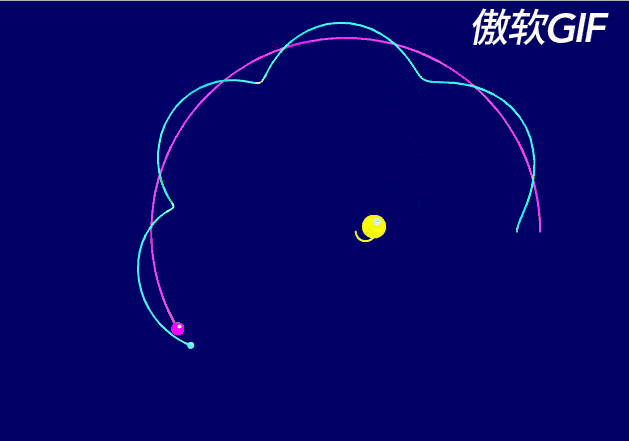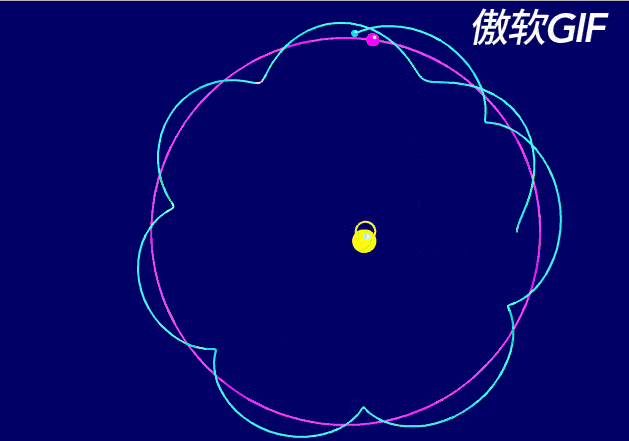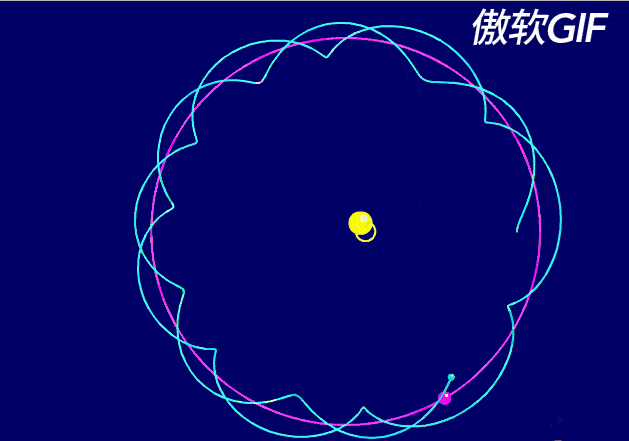
当然,这个动图的轨道比例,依旧过大。
实际日地月系统的轨道变化,远远微小得多。
如果我们把地球的半径6378.137km缩小为1cm,那么月球半径1737.10km相当于0.27cm,太阳半径的6.955×10^5 km则相当于1.09m。
而月地距离为0.6m,日地距离相当于234.55m。
也就是说一个,日地月相当于这样的比例:
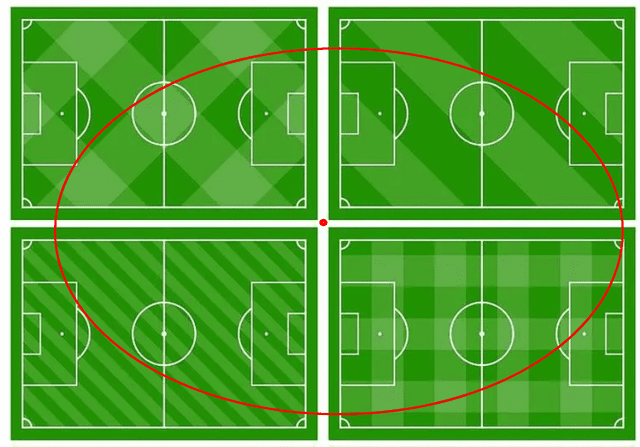
四个标准足球场拼在一起,长度200多米,太阳在中间像一个半径1米的大火球。地月距离小于太阳半径,只有0.6m,因此整个地月系统,都仅仅相当于那一条红线。
也就是说,月球绕着太阳的“花边”运动,朔望日之间的距离差,小至红线范围内。
相对于太阳,朔日月球速度为28.757km/s,望日速度为30.803km/s。朔望日之间的速度变化,也并不大。
真实效果会是这样的:
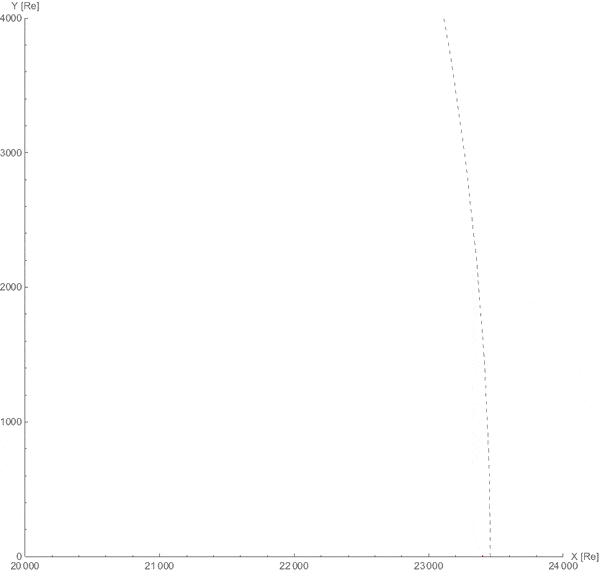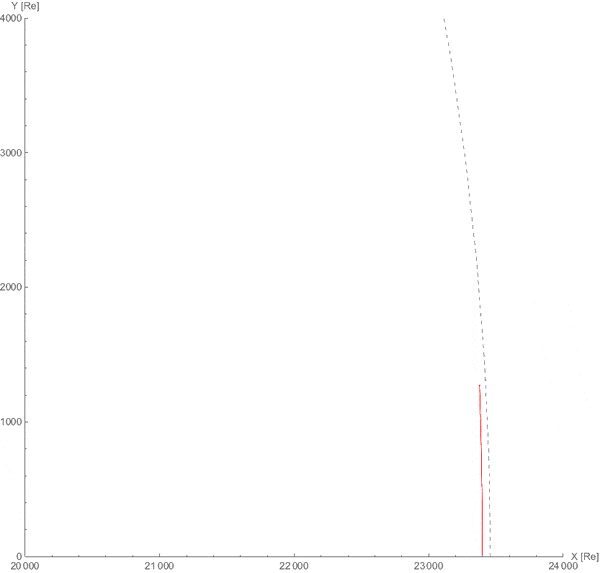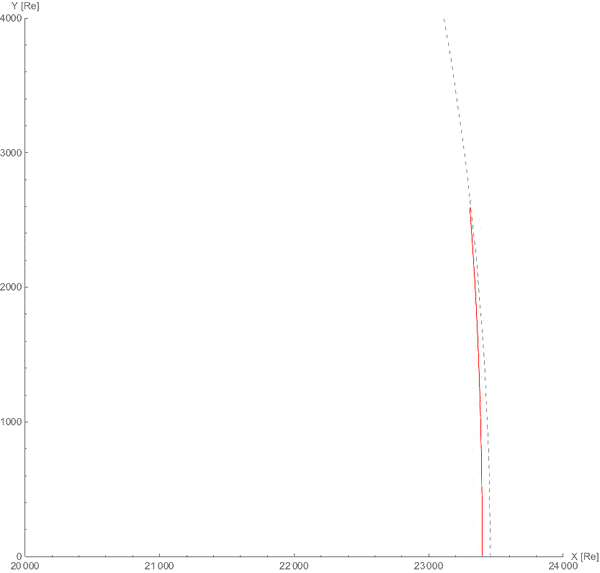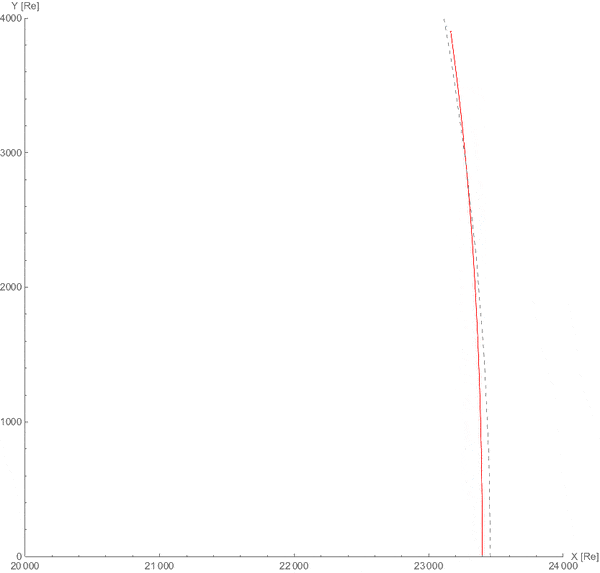
因此,在足够大尺度观察月球,日月轨道和日地轨道几乎可以等同处理。
当然,即便等同处理,也是以地日轨道为准。
其实,如果我们把整个视角放大到整个银河系。
整个太阳系绕银河系运动的速度高达250km/s,相当于水星绕太阳运动速度47.87km/s的5倍还多。
由于地球公转的黄道面与银道面有着60°左右的夹角:
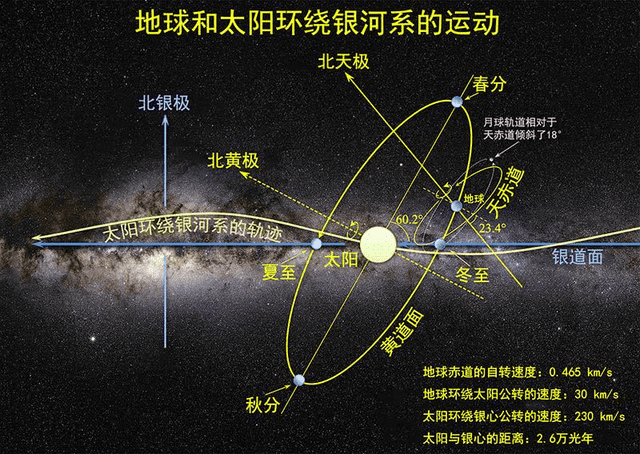
因此太阳系的行星,如果单独拿出来绘制出它们与银河系的轨道,将会是一个由更多细小螺旋“花边”组成的漫长轨道(太阳2.5亿年绕银河系一周,地球轨道附近以内的星体都能绕出数亿的螺旋“花边”)。

虽然所有星系都围绕着银心运动,包括这些星系内的行星以及卫星,但我们通常不说地球的中心天体是银心。
这本质上相当于:B是A的中心天体,C是B的中心天体,虽然C不是A的中心天体,但C是随着B围绕A运动的。
总之,地球是月球的中心天体,与月球同时围绕着太阳转并不矛盾。
本文来自微信公众号:瞻云(ID:zhanyun2028),作者:瞻云

