1936年,英国数学家阿兰·图灵提出了通用计算机的想法。那是一个简单的装置:一条无限长的磁带,上面写满了0和1,还有一台机器,可以沿着磁带来回移动,按照一定的规则将0变为1,反之亦然。他证明,这样一个装置可以用来进行任何计算。
图灵并不打算将他思想实验里的机器用于解决实际问题。相反,它是为探索计算的本质及其极限提供了一种宝贵的方法。在这一开创性想法提出后的几十年里,数学家们提出了一系列实用性更低的计算方案。原则上,如经典的《扫雷》或《万智牌》这样的游戏都可以用作通用计算机。约翰·康威(John Conway)的 “生命游戏”(Game of Life)等所谓的元胞自动机也是如此,后者是一套在二维网格上演化黑白方格的规则。
关于生命游戏与元胞自动机
英国数学家约翰·何顿·康威在1970年发明了一种二维的细胞自动机,它可以模拟生命的演化和复杂性。
生命游戏的规则非常简单,只涉及每个像素点的存活(亮)和死亡(暗),以及它们与周围8个细胞的互动。具体来说,每个像素点,我们叫它细胞,有两种状态:存活或死亡。每个细胞在下一个时刻的状态取决于以下四条规则:
1. 如果一个细胞周围有少于两个存活的细胞,它会因为孤独而死亡。
2. 如果一个细胞周围有两个或三个存活的细胞,它会继续存活。
3. 如果一个细胞周围有超过三个存活的细胞,它会因为拥挤而死亡。
4. 如果一个死亡的细胞周围有正好三个存活的细胞,它会重新复活。
康威的生命游戏的魅力在于,它用极其简单的规则,却能产生出极其复杂和多样的现象。在游戏的进行中,可以出现各种各样的细胞结构,有些是稳定的,有些是周期性的,有些是移动的,有些是增长的,有些是互动的,甚至有些是可计算的。
虽然很抽象晦涩,但这段视频实际上是在用康威的《生命游戏》中构建的宇宙飞船形态搜索素数的过程。也就是说,我们把《生命游戏》变成了一个可以运行计算素数程序的广义计算机。这些飞船正好代表质数。它是由迪恩·希克森(Dean Hickerson)于1991年发明的。丨图源:Conway's Game of Life (conwaylife.com)
2023年9月,康奈尔大学的英娜·扎卡雷维奇(Inna Zakharevich)和富兰克林与马歇尔学院的托马斯·赫尔(Thomas Hull)证明,任何可以计算的东西都可以通过折纸来计算。他们证明了折纸是“图灵完备”的——这意味着,就像图灵机一样,只要有足够的时间,它就能解决任何可计算的问题。
扎卡雷维奇是一名折纸爱好者。2021年,她在偶然看到一段解释“生命游戏”图灵完备性的视频后,开始思考这个问题。“我当时想,折纸比生命游戏复杂得多。”扎卡雷维奇说,“如果生命游戏是图灵完备的,那么折纸也应该是图灵完备的。”
计算的本质
科学界有一种小众主张,叫广义的计算主义世界观(狭义的计算主义是一种认识论)。其中最激进的鼓吹者如沃尔夫勒姆(开发了著名的数学软件Wolfram Mathematica的Stephen Wolfram),认为整个宇宙不过是台元胞自动机。我们的物理学规律、乃至物质本身,都是某种计算结果涌现。就和生命游戏一样。而真正的科学是寻找核心的计算规则。他在最近两年甚至证明出,热力学第二定律就是特定计算规则的结果。
考虑到计算的普遍性,我们甚至很难说他的观点是错的。
常见的计算的例子有数学方程和计算机算法。执行具体计算的机械或电子设备(或者历史上的人)被称为(狭义上的)计算机。
良定义(well-defined)是指一个数学陈述或计算可以被明确地表达为一个图灵机的初始参数。图灵机是一种抽象的计算模型,可以模拟任何可计算的过程。因此,任何具有良定义性质的数学陈述或计算都被称为可计算的(computable),而陈述或计算本身被称为计算(computation)。此类研究构成了可计算性领域,它是数理逻辑和计算机科学的一个子领域。
但是,计算也可以被看作发生在一个封闭的物理系统中的纯物理过程。图灵在1937年的证明表明,可计算陈述和特定的物理系统之间存在着形式上的等价性,这些物理系统也被一并称为(广义上的)计算机。
那对一张纸按一些常见的规则进行折叠,这一操作也可以把纸变成计算机吗?
可惜的是,计算科学并不是扎卡雷维奇的专业领域。虽然她从小就喜欢折纸——“如果你想给我一个超级复杂的东西,需要一张24英寸的纸,有400个步骤,我都会亲手操作一番。”但她的数学研究涉及代数拓扑学和范畴论等更为抽象的领域。于是,她给全心研究折纸数学的赫尔发了电子邮件。
“她突然就给我发了邮件,我当时就想,为什么一个代数拓扑学家会问我这个?”赫尔说。但他意识到自己从未想过折纸是否可能是图灵完备的。“我当时想,可能是如此,但实际上我并不确定。”
于是,他和扎卡雷维奇开始证明,折纸可以转化成计算机。首先,他们必须将计算输入和输出以及AND和OR等基本逻辑运算编码成用纸折出的构型。如果他们能证明他们的方案可以模拟其他已知图灵完备的计算模型,那么他们就达到了目的。
关于折纸
折纸,在国人看来或许是些不登大雅之堂的雕虫小技,学龄前儿童玩玩就算了,上了学,一般就没时间玩折纸了。日本人却不这么看。他们把折纸视为国粹,不但有折纸协会,还把折纸列为了全国小学必修科目。日本人并不是因为折纸属于传统艺术,就决定将它列入必修课的;同是该国传统艺术的插花、茶道,就没有被列入必修课。
20世纪70年代,日本学者吉泽章(Akira Yoshizawa)将目光投向折纸中的数理,之后在日本形成了一个研究折纸数理的高潮,结成了多个研究团体,也出版了许多的专著。
这些早期研究者惊喜地意识到,折纸甚至可以解三次以内方程,至于1/n这种有理数自然是可以求(表示)出来的;不仅如此,折纸可以解决三等分角和倍立方体这两个尺规作图不能解的问题(然而还是不能解决化圆为方,因为π是超越数)。
到今天,在学术领域,折纸已经得到了相当多的数学分析。人们感兴趣的领域包括特定纸模型的平整可折叠性(立体模型能否在不损坏的情况下被压成平面),以及用折纸法求解有理方程。
此外还有著名的餐巾折叠问题:是否可以把一张正方形或长方形的纸折叠成一个平面图形,使得它的周长大于原来的正方形。
如果对折好的纸作品进行剪切的话,我们还有美妙的折叠和切割定理:任何具有直边的形状都可以通过从单张(理想化)纸上将其折叠平整并进行单个直线完全切割而来。这些形状包括多边形(可以是凹形的)、带孔的形状以及此类形状的集合(即区域不需要连接)。
计算折纸学是计算机科学的一个最新的分支,主要研究解决折纸问题的算法。自20世纪90年代罗伯特·朗(Robert Lang)提出TreeMaker算法以帮助精确折叠底座以来,计算折纸领域也取得了长足的发展。在折纸可折叠性问题中,目标是利用初始构型的折痕折叠某物。折纸设计问题的结果比折纸可折叠性问题的结果更容易理解。计算折纸对数学和计算机图形学方面知识的要求很高,而且在航空材料等很多领域都有巨大贡献,并不只是停留在折纸工艺品的层面上。
不过上述技术本质上是基于几何的——针对具体问题给出明确而巧妙的构造,扎卡雷维奇与赫尔现在则是希望了解,借助一些显而易见的折纸规则,能否通过折叠一张纸,从理论上实现图灵机的抽象功能?
逻辑运算接受一个或多个输入(每个输入都写成“真”或“假”),并根据给定的规则输出“真”或“假”的值。为了在“纸上”进行运算,数学家们设计了一个名为折痕模式的线条图,规定了折痕的位置。纸上的褶代表输入。如果沿着折痕图案中的一条线折叠,褶皱就会翻转到一边,表示输入值为“真”。但如果沿着不同的(附近的)线折叠纸张,褶皱就会翻转到其反面,表示“假”。
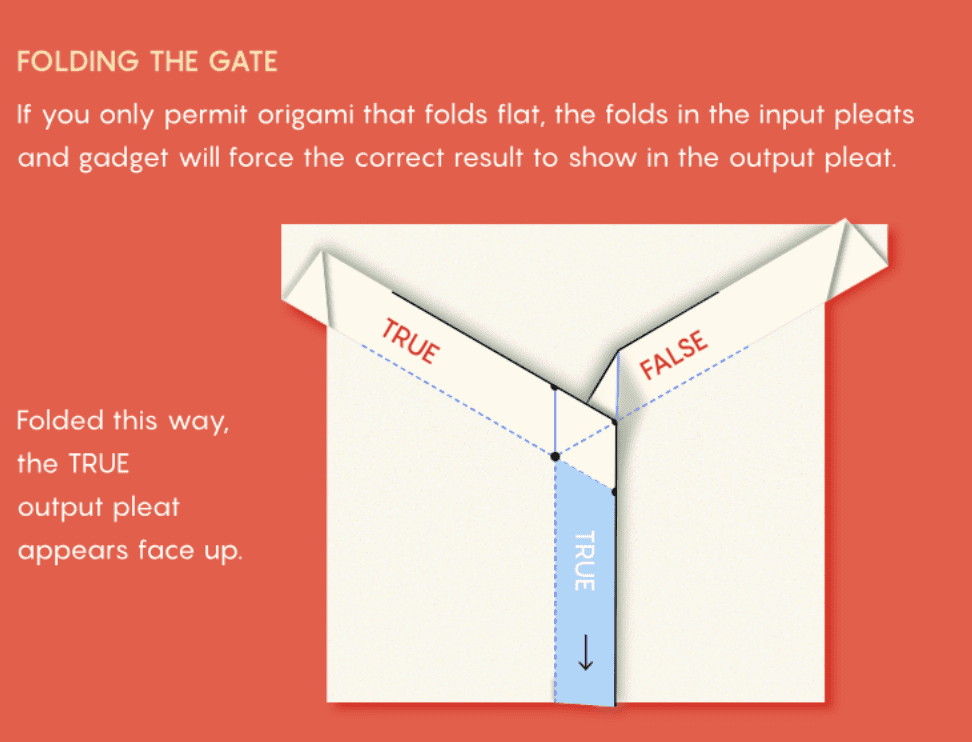
代表逻辑真值的折痕与褶皱丨图源:quantamagazine
其中两个输入褶被送入一个复杂的褶皱数学编译小工具。小工具对逻辑运算进行编码。为了在完成所有这些折叠的同时还能使纸张折叠平整——这是赫尔和扎卡雷维奇提出的要求——他们加入了第三个褶皱,迫使它以特定的方式折叠。如果褶皱以一种方式翻转,则表示输出为“真”。若翻转向另一侧,则输出为“假”。
数学家们设计了不同的小工具,根据各种逻辑运算将输入转化为输出。赫尔说:“我们在纸上玩了很久,互相发送图片……然后写出严格的证明,证明这些东西按照我们所说的方式运作。”
自20世纪90年代末以来,人们就知道康威生命游戏的一个更简单的一维类似物是图灵完备的。赫尔和扎哈雷维奇想出了如何用折纸代表的逻辑运算来编写这个版本的“生命”游戏。“我们最终只需要使用四个门:AND、OR、NAND和NOR。但要将这些不同的门组合起来,他们必须制造新的小工具,吸收无关信号,并允许其他信号在不相互干扰的情况下转向和交叉。”扎卡雷维奇说。
扎卡雷维奇认为,这是最困难的部分。要想办法让所有东西都正确地排列在一起。在她和赫尔成功地将他们的小工具组装在一起后,他们可以将所需的一切都编码在纸张折叠中,从而表明折纸是图灵完备的。
折纸计算机的效率非常低,而且不切实际。但从原理上讲,如果我们有一张很大的纸和大量的时间,你可以用折纸计算出任意多位数的π、确定世界上所有送货司机的最佳路线,或者运行一个预测天气的程序。赫尔说:“最终,折叠次数将非常巨大。在物理上很难完成,但理论上它能完美工作。”(真实世界里的纸,我们都难以把它对折7次!)
有用与无用的折纸数学
几十年来,数学家们被折纸所吸引。在麻省理工学院计算机科学家埃里克·德梅因(Erik Demaine)看来,“它看起来既有趣又无用”。
计算几何——计算折纸学里划时代的论文出自1999年,正是埃里克·德梅因——那时的滑铁卢大学博士研究生——描述了一种能决定如何将一张纸折为任何可想象到的三维形状的算法。但这种方法并没有得出非常实用的折叠模式,主要在于阐明了理论上的可行性。
在2017年7月举行的计算几何学讨论会上,德梅因和东京大学的计算几何学家舘知宏(Tomohiro Tachi)又找到了接缝最少的算法。

研究人员创建了一种用于折叠折纸形状的通用算法,可以保证最少的接缝数量。丨图源:Christine Daniloff/麻省理工学院
美国数学会成员罗伯特·朗是当代最富盛名的折纸数学和计算机折纸学研究者,他证明了无论多么复杂的折纸作品,都可以通过数学来建模。他撰写的著作Origami Design Secrets被誉为折纸的圣经。
但最近,折纸也吸引了工程师的目光。
在折纸数学领域,存在若干非常著名的问题。如刚性折纸的问题,把折痕看成是铰链,折痕两边的纸区域是两个被铰链连接的刚性平面。这方面的研究具有很大的实用价值。如Miura地图折叠是一种刚性折叠,早已用于为太空卫星部署大型太阳能电池板阵列。

在过去,卫星天线是使用四叠或八叠法。然而,这折叠方法非但在运作时需繁复的工序,更浪费不少空间,又容易损耗,需经常维修和保养。为此,日本学者三浦公亮(Miura)致力于发明一种能解决上述问题的新技术。结果,他发现椭圆筒表面的褶皱构造有利于节省空间又能避免损耗,而且强度高[3]。这最终使他发明了“拉开对角两端来把物品展开,而在收缩时则反向推入”的折叠方法。丨图源:Miura fold - Wikipedia
折纸数学已被用于设计可折叠并运入太空的大型太阳能电池板、可在水中游泳以收集环境数据的机器人、可在微小血管中穿行的支架,以及模拟DNA折叠工具等。德梅因说:“现在有成百上千的人在使用我们开发的所有折纸数学和算法来设计新的机械结构。”
因此,“我们越是做这样的事情,”赫尔说,“我认为我们就越有机会在折纸和成熟的数学分支之间建立深度交叉。”
补充内容:利尔法折纸解三次方程
在数学中,利尔法是一种寻找任意次幂一元多项式实根的直观方法,由奥地利工程师爱德华·利尔(Eduard Lill)于1867年提出。后来折纸几何的研究者意识到,这一技术恰好也是折纸解三次方程的核心算法。下面主要展示利尔如何把多项式和方程的根直观化。略过具体折纸过程和证明。
利尔的方法是画成直角的直线段,每条长度等于多项式的系数。多项式的根可以通过其直角路径的斜率找到,这些路径也连接起点和终点,但顶点在第一条路径的直线上。
用折纸求整系数三次方程 4x3+2x2-2x-1=0的根-1/2、-1/√2 和 1/√2,重点在于直观显示如何处理负系数和延长线段。
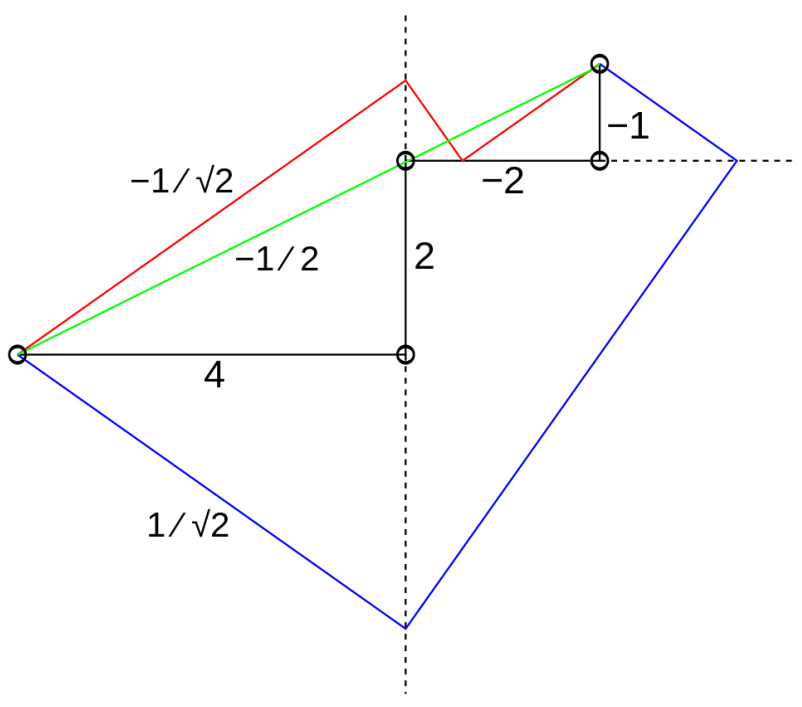
三次代数方程的图示法丨图源:Lill's method - Wikipedia
要使用这种方法,需要从原点开始画图。根据第一个系数(最高幂项的系数)的大小向右画一条线段(因此,如果系数为负,线段的终点将在原点的左边)。从第一条线段的末端开始,按第二个系数的大小向上绘制另一条线段,然后按第三个系数的大小向左绘制,再按第四个系数的大小向下绘制,以此类推。
方向(不是转折)的顺序总是向右、向上、向左、向下,然后重复。因此,每一圈都是逆时针方向。多项式的每个系数(包括零)都是如此,负系数则“倒着走”——例题正是有负系数的情况。最后到达的点,也就是方程常数项对应线段的末端,就是终点。
再按照一定的规则画出图里的彩线。以红线为例,它构成的折线直角都是90°,且红线最终也要落在终点上。如果能够确定红线,就能借助对称性,确定和原点相连的第一条蓝线,然后根据直角折线找到蓝线的终点。
彩色线上显示的每个数字都是其斜率的相反数,也是多项式的实数根。
所以,问题本质上就是用折纸的方法,确定由原点出发的那段红线的斜率,保证红线折线段最后可以落在终点上。具体论证比较繁复,有兴趣的朋友可以见参考[7]里的详细资料。
参考文献:
[1] [2309.07932v1] Flat origami is Turing Complete (arxiv.org)
[2] How to Build an Origami Computer | Quanta Magazine
[3] Mathematics of paper folding - Wikipedia
[4] 折り紙公理 - Wikipedia
[5] TT's Page (tsg.ne.jp)
[6] Lill's method - Wikipedia
[7] 折纸数学-扔掉工具,你能走的更远(四)莉儿法则 - 哔哩哔哩 (bilibili.com)
[8] Nathaniel Johnston » Generating Sequences of Primes in Conway's Game of Life
本文受科普中国·星空计划项目扶持,出品:中国科协科普部,监制:中国科学技术出版社有限公司、北京中科星河文化传媒有限公司
本文来自微信公众号:返朴 (ID:fanpu2019),作者:嘉伟

