1900年,希尔伯特(David Hilbert)在题为《数学问题》的讲演中,提出了23个公开问题[18]。其中的第15个问题,专注于19世纪计数几何与相交理论,题目是“为舒伯特计数演算法建立严格基础”。
Springer数学百科全书[28]中回顾到:“澄清舒伯特演算是20世纪代数几何学的重要主题”。本文旨在寻根溯源,以几何学拓荒者们的故事为掠影,对第15问题的解答为脉络,重现代数几何学的诞生历程。
一、相交理论简史
公元前3世纪,希腊几何学家阿波罗尼斯(Apollonius, 262-190 B.C.)在“Tangencies”一文中,证明了下述结果。是计数几何学的第一个范例:
定理1.1:对于平面中处于一般位置的3个圆,恰有8个圆与它们相切。

阿波罗尼斯定理的示意图
这个定理的最初证明已遗失在历史的尘埃中,后人仅能从帕普斯(Pappus)在公元4世纪的一篇记述中得知这个结果。在文艺复兴时期,众多几何学家致力于寻求该定理的证明,其中韦达(Viete),阿德里安(Adriaan van Roomen), 热尔冈(Joseph Diaz Gergonne)和牛顿(Newton)取得了成功。上面的插图是剑桥大学2016年出版的代数几何教程《3264 及相关故事》[15]的封面故事,其中的数目3264,系指复射影平面中与5条处于一般位置的圆锥曲线相切的圆锥曲线的条数,由Chasles在1864年得到[2]。
笛卡尔(Descartes, 1627)空间坐标系的发现,使得几何学家们(如Maclaurin(1720),Euler(1748),Bezout(1764))能够利用多项式方程组,来刻画满足特定几何条件的几何对象。于是,许多计数几何问题有了如下表述:
多项式问题:对于复数域上一个自变量的个数等于方程的个数的多项式方程组:
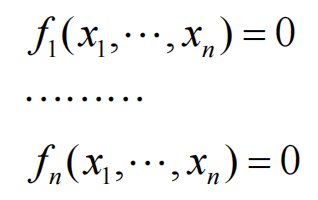
求它的解的个解(包括重数)。
多项式问题是代数学中一个基本问题。例如,高斯(Gauss)曾在1820年证明:复数域上一个单变量n次多项式方程f(x)=0恰有n个解,被后人称为“代数学基本定理”。
设gi是多项式fi(x1,…,xn)=0的齐次化,我们得到n维复射影空间M=CPn中一张超曲面:
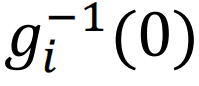
一般说来,复射影空间上一个齐次多项式方程组零点的集合称为一个射影代数簇。于是,多项式问题自然导致了相交数问题。
相交数问题: 已知光滑复射影代数簇M中处于一般位置的k个子代数簇N1,…,Nk,满足维数条件:
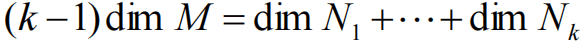
求它们在M中相交点的个数。
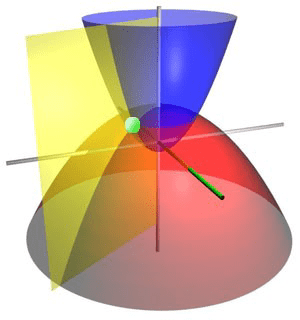
相交理论示意图
相交数问题的提出可归功于法国力学家、数学家庞斯列(Jean-Victor Poncelet, 1788~1867)。他于1811年毕业于巴黎理工大学,作为工程兵上尉参加了拿破仑侵俄战争。在莫斯科附近的克拉斯诺耶战役中,被误认为阵亡而被遗弃在战场,被俘后囚禁在西伯利亚Saratow战俘营。
庞斯列通过研究几何学度过了战俘营中的艰难岁月。他仅靠大学期间蒙日(Monge)所教授的画法几何学的基础,在对17世纪射影几何一无所知的情形下,独立发现并建立了高维射影几何学的系统理论。他提出并研究了图形经过中心射影的不变性质;引入了“交比”的和“无穷远”元素的概念;建立了二次曲线和曲面的配极理论,并由此得到一般的对偶原理。
此外,他还研究了图形在一定范围内连续变动时所保持的性质,提出了“连续性原理(the principle of continuity)”,这是今天拓扑学中的“相交数同伦不变性”以及代数几何中的“Chow's moving lemma”的雏形。庞斯列将他在战俘营期间的工作整理为《论图形的射影性质,1816》一文,这是近代射影几何以及相交理论的奠基性工作。但柯西对庞斯列参加法国大革命的经历十分不满,以文章会导致“严重错误”为由,拒绝发表该文。
1900年,庞加莱在3维流形的分类工作中,创造性地引入了流形M的同调群H*(M),使得人们能够应用群中的运算来解析M的几何结构。在研究相交数问题的过程中,莱夫舍茨(Lefschetze)进一步建立了流形M的上同调理论H*(M)[21,1926]。从链复形的层次看,后者只是前者的对偶,但与同调论相比较, 上同调具有一个突出优势:对角映射d:M→MxM诱导了上同调群中一个称为“杯积”的乘法运算:
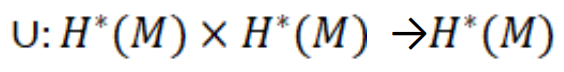
这使得H*(M)成为一个分次环。正是这个乘法运算,为相交数问题的解答,提供了一个普遍性的公式。沿用前面的记号,我们用下列式子来表示子簇Ni在同调群中的基本类,并用符号αi表示它在上同调中的庞加莱对偶(Poincare dual):
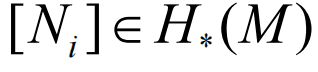
相交理论基本问题:已知光滑复射影代数簇M中处于一般位置的k个子代数簇N1,…,Nk,满足维数条件:
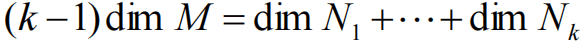
求Kronecker赋值:
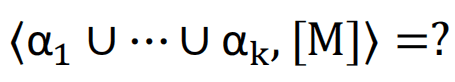
至此,我们回顾了历史上解答计数问题(或相交数问题)的三个设想,以及它们之间一脉相承的关系。自然地引出了一个问题,哪种方案具备有效可算性?这不仅是计数几何问题的核心要求,也是推动20世纪代数几何学发展的动力。
二、希尔伯特第15问题
舒伯特(Hermann Schubert, 1848~1911)于1870年在德国哈勒大学(the University of Halle)获得博士学位。他的博士论文《特征数理论》[22]的主题是计数几何学。此前,他已发表过相关文章,证明了空间中与4个处于一般位置的球面相切的球面有16个,是阿波罗尼斯定理在空间情形的直接推广。
1879 年,舒伯特发表了19世纪相交理论的巅峰之作《计数几何演算》[23]:

舒伯特与《计数几何演算》
在该书中,他发展了 Chasles 关于圆锥曲线的工作[2],并通过一系列示例, 展示了相交理论的几何魅力。例如:
例2.1: 给定空间中处于一般位置的8张二次曲面,恰有4407296条圆锥曲线与它们相切;
例2.2: 给定空间中处于一般位置的9张二次曲面,恰有666 841 088张二次曲面与它们相切;
例2.3: 给定空间中处于一般位置的12张二次曲面,恰有5819539783680条三次立体曲线与它们相切。
由于舒伯特的工作广泛应用了柯西所反对的“连续性原理”,广受非议。为了回避批评,他在1874年将该原理更名为“特殊位置原理(the principle of special position)”,两年后又更名为“数的守恒原理(the principle of conservation of numbers)”;仍然受到Study和Kohn的攻击[19]。最为中肯的评论来自范·德·瓦尔登(van der Waerden),他在文献[32]中回顾道,舒伯特的论证如此之概略,以至于“没有给出相交数的定义,没有办法找到它,也没有办法计算它”。
希尔伯特在第15问题中要求,“为舒伯特计数演算法建立严格基础”。同时,希尔伯特肯定了舒伯特的方法能够预见到多项式问题的解的优势:
“这个问题是:对于计数几何中的那些几何数目,在准确界定其适用范围的前提下,严格地证明其正确性。特别需要研究的是,舒伯特在他的书中,基于所谓特殊位置原理(或相交数的守恒原理)所建立的一套计数演算法,并据此算出的那些几何数目。
虽然今天的代数学在原则上保证了实施消元法的可能性,但要证明计数几何中的那些定理,对于代数学提出了更高要求。因为,它要求在对那些特定的方程(组)实施消元法之前,事先就能预见到最终所得方程的次数及其解的重数。”

希尔伯特与第15问题
三、舒伯特演算的基本问题:特征数问题
为深入到舒伯特演算的核心内容,我们引用原著[23]中一个计数表格:
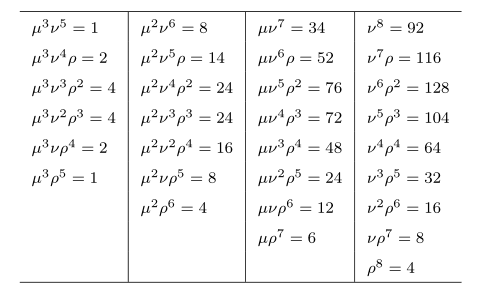
表1. 空间圆锥截线的特征数方程
其中,符号ρ, μ, ν依次表示空间中通过一个定点、相交于一条定直线、相切于一张定平面的圆锥截线所构成的三个代数簇。舒伯特本人将表格中的等式称为“特征数方程”,而早期的研究者也称它们为“舒伯特符号方程”。舒伯特在他的工作[22~24]中多次强调,特征数问题是计数几何的主要理论问题[20]。然而,为了得到“特征数问题"的严格表述,数学家们用了60多年时间,本节回顾一下相关故事。
1. 意大利学派(The Italian school)
首先研究第15问题的数学团体,是以恩里克斯(Enriques)和塞韦里(Severi)为代表的意大利学派。他们的代表性著作是塞韦里的文章《(特征)数的守恒原理》和《计数几何基础与特征数理论》[26, 27]。根据范·德·瓦尔登[28]的记述,“他们建立了令人钦佩的结构,但逻辑基础不稳定,概念定义不明确,证据也欠充分”。

意大利学派关于相交理论进行辩论的场景
2. 哥廷根学派(The Gottingen School)
1930年,范·德·瓦尔登发表了“计数几何演算的拓扑基础”[29]一文,是代数几何发展史中的一个重要里程碑。他在文章中首次提出,在莱夫谢茨所建立的上同调理论的框架中,解答第15问题的设想。他在文章中敏锐指出:
(1)每个舒伯特符号方程应是某个射影类流形上同调群中的一个关系式;
(2)解答特征数问题的前提,是确定该射影流形上同调群的一个加法基底;
(3)所有计数问题的共同目标,是计算射影类流形中代数簇的相交数,成功地引领了第15问题的后续研究。

范·德·瓦尔登与《计数几何学的拓扑基础》
3. 布尔巴基学派(Bourbaki)
设G是一个紧致连通李群,P是G的一个抛物子群。通过G到它的李代数的伴随表示,齐性空间G/P得以实现为一个光滑复射影代数簇,称为李群G的一个旗流形。下面,我们依从文献[1],用W(G)表示李群G的外尔群(Weyl group),并用W(G;P) 表示子群W(P) 的左陪集W(G)/W(P)。由埃里斯曼(C. Ehresmann )在1934年首度发现:[14]
(1)舒伯特演算所关心的几何对象的参数空间,本质上是旗流形 G/P 的一些特例;
(2)对于复格拉斯曼类流形 Gn,k(C) 这个特殊情形,经典的舒伯特符号,恰好是其上同调群的一个加法基底。
随着研究的深入,早期文献中的含糊术语“舒伯特符号”,逐步被“舒伯特胞腔”或“舒伯特簇”此类严谨的几何对象所替代。尤其是,切瓦利(Chevalley)、盖尔芳德等人相继证明,每个旗流形G/P具有一个胞腔分解:
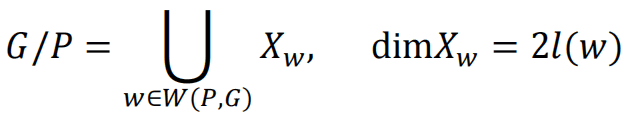
其中XW是W(P,G)中元素w所决定的舒伯特胞腔(簇),l:W(G, P)→Z是长度函数。由于上述分解中只涉及偶数维胞腔,全体舒伯特胞腔(簇)的基本类[XW]的Kronecker对偶SW,称为舒伯特类(Schubert class),构成了上同调群H*(G/P)的一个加法基底。我们立即得到:
定理3.1(舒伯特演算的基底定理):对于每个旗流形G/P,它的全部舒伯特类是上同调群H*(G/P)的一个加法基底。
根据基底定理,旗流形G/P中的任意一组舒伯特类SW1,…,SWk的乘积,可唯一表示为舒伯特基底的整系数线性组合:
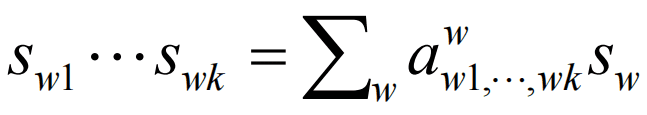
其中:
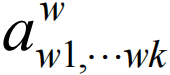
上式的系数正是舒伯特意义下的特征数。至此,特征数问题[20, 22, 23, 24]得到了简洁且严格的表述:
问题3.2(特征数问题:The problem of characteristics):对于旗流形G/P的每个舒伯特类的单项式SW1,…,SWk,求出所有系数的值:
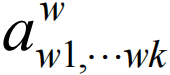
令人惊奇的是,在上同调理论正式诞生的前50年,舒伯特就已经在应用该理论,从事计数几何演算工作。作为例证,我们援引柯立芝[4]的一段记述:“舒伯特所面临的基本问题,是将这些符号的乘积用其他符号线性表出。他仅取得了部分成功。”
四、代数几何学的诞生
范·德·瓦尔登在文章[30]的开篇中指出:“第15问题的核心问题在于给出相交重数(intersection multiplicities)的定义(或计算公式),借助该公式,我们能够有效计算出舒伯特的那些计数几何问题的解,同时使得相交数的守恒原理得以保持”。随之,他开始了构建代数几何学基础的规划。
他在《Mathematische Annalen》上发表了系列文章《ZurAl- gebraische Geometrie(#1~#20)》,并在1939 年出版了名著《Introduction to Algeberaic Geometry》,首要任务是寻求“相交重数”的严谨定义。
安德烈·韦伊(Weil.A)是布尔巴基学派的灵魂。1946年,他发表了里程碑式的名著《代数几何基础》[31],其中第一次系统且完整地对于代数闭域上的代数簇,给出了“相交重数”的定义。随后,他根据切瓦利所发现的舒伯特演算的基底定理(定理3.1),在该书的第二版中,将希尔伯特第15问题的解答,等价于“决定所有旗流形G/P的上同调环” 的问题[31, p.331]。下称为“韦伊问题”。

韦伊与《代数几何学基础》
在韦伊工作[31]的基础上,对于不可约代数簇W中两个维数互补子簇X, Y, 塞尔(Serre J.P.)得到了相交重数的“优美公式” [25, 1965]:
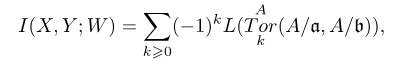
其中A表示局部环O(X,W),a和b依次是代数簇X和Y的理想,L是A模的长度。随后,富尔顿(Fulton W)和麦克弗森(MacPherson R.D.)一道,将公式推广到带奇点的代数簇[16]。遗憾的是,此类公式无法从事有效计算,尤其是第15问题所关切的特征数的计算。
第15问题是当代数学中一个影响深远的问题,它推动19世纪的计数几何与相交理论,成长为20世纪数学大师范·德·瓦尔登和安德烈·韦伊所建立的代数几何学[29~31],使得舒伯特演算深度融入微分几何学、代数拓扑学、李群表示论等领域,深刻地影响着这些领域的发展轨迹。这一切,既是希尔伯特对于数学发展的宽阔视野和前瞻性的有力见证,也对探索舒伯特演算行之有效的演算法则,尤其是特征数问题和韦伊问题的解答,提出迫切要求。
1931年,周炜良(Wei-Liang Chow, 1911~1995)在芝加哥大学获博士学位。出于对范·德·瓦尔登《代数学》的欣赏,他在1933年赴德国莱比锡大学,跟随范·德·瓦尔登研究代数几何学。1958年,他在切瓦利(C. Chevalley)的讨论班上宣布了以他的姓氏所命名的周环(Chow Ring)[4],是当代相交理论的一个基础平台。
周炜良在构建周环的工作中,证明了所有旗流形周环A*(G/P)和上同调环H*(G/P)之间,存在一个典范同构。利用这个同构,段海豹、赵学志在他们的系列工作[6~11]中,发展了微分拓扑、代数拓扑、以及符号计算的技术,从理论到计算两个角度,解决了“特征数问题”和“韦伊问题”。据此,他们已在文章[12,13]中阐明,第15问题已获解答。
参考文献:
[1] Bernstein I N, Gel'fand I M, Gel'fand S I., Schubert cells and cohomology of the spaces G/P, Russian Math. Surveys, 28: 3 (1973), 1--26.
[2] Chasles M., Construction des coniques qui satisfont à cinque conditions, C. R. Acad. Sci. Paris, 58(1864), 297--308.
[3] Chevalley C., Sur les Decompositions Celluaires des Espaces G/B, Proc. Symp. in Pure Math. 56 (part 1) (1994), 1--26.
[4] Coolidge J.L., A history of geometrical methods, Oxford Univ. press,1940.
[5] Chow W. L., Anneaux de Chow et applications, Sem. Chevalley (1958).
[6] Duan H., The degree of a Schubert variety, Adv. in Math., 180(2003), 112--133.
[7] Duan H, Zhao X., Multiplicative rule of Schubert classes, Invent. Math. 159(2005), no. 2, 407--436; 177(2009), no.3, 683--684.
[8] Duan H., Multiplicative rule in the Grothendieck cohomology of a flag variety, J. Reine Angew. Math. 600 (2006), 157--176.
[9] Duan H., Zhao X., A unified formula for Steenrod operations in flag manifolds. Compos. Math. 143(1), (2007), 257--270.
[10] Duan H, Zhao X. The Chow rings of generalized Grassmannians, Found. Math. Comput. 10(2010), no.3, 245--274.
[11] Duan H, Zhao X., Schubert presentation of the cohomology ring of flag manifolds G/T, LMS J. Comput. Math. 18(2015), no.1, 489--506.
[12] Duan H, Zhao X., On Schubert's Problem of Characteristics, in Schubert calculus and its applications in Combinatorics and representation theory, Springer proceedings in Mathematics and Statistics, Vol. 332(2020), 43--71.
[13] Duan H, Zhao X., Schubert calculus and interesection theory of flag manifolds, Russian Math. Surveys (Uspekhi Matematicheskikh Nauk), 77(2022), 729--751.
[14] Ehresmann C. Sur la topologie de certains espaces homogenes, Ann. of Math. (2) 35 (1934), 396--443.
[15] Eisenbud D, Harries J., 3264 and all that: A Second Course in Algebraic Geometry, Cambridge University Press, 2016.
[16] Fulton W,. MacPherson R.D., "Defining algebraic intersections", LNM. 687, 1978.
[17] Fulton W., Intersection theory, Springer-Verlag, 1998.
[18] Hilbert D., Mathematische Probleme, Bull. AMS. 8(1902), 437--479.
[19] Kleiman S., Problem 15: Rigorous foundation of Schubert's enumerative calculus, Proc. Symp. Pure Math., 28, Amer. Math. Soc. (1976), 445--482.
[20] Kleiman S., Book review on ``Intersection Theory by W. Fulton'', Bull. AMS, 12(1985), no.1, 137--143.
[21] Lefschetz S., Intersections and transformations of complexes and manifolds, Trans. AMS, Vol.28, no.1 (1926), 1--49.
[22] Schubert H., Zur Theorie der Charakteristike, Celles Journ. 71(1870), 366--386.
[23] Schubert H., Kalkul der abzahlenden Geometrie, Berlin, Heidelberg, New York: Springer-Verlag (1979).
[24] Schubert H., A Losung des Characteristiken-Problems fur lineare Raume beliebiger Dimension, Mitteilungen der Mathematischen Gesellschaft in Hamburg, t. I (1886), pp. 134–155.
[25] Serre J.P., Algebre Locale, Multiplicites, LNM, 11, 1965.
[26] Severi F., Il Principio della Conservazione del Numero. Rendiconti Circolo Mat. Palermo 33, 313 (1912).
[27] Severi F., Sui fondamenti della geometria numerativa e sulla teoria delle caratteristiche,
Atti 1st. Veneto, 75 (1916), 1121-1162.
[28] Sottile, F., Schubert calculus, Springer Encyclopedia of Mathematics, 2001.
[29] van der Waerden B L., The foundation of algebraic geometry from Severi to Andre Weil, Archive for History of Exact Sciences, 1971.
[30] van der Waerden B L., Topologische Begrundung des Kalkuls der abzhlenden Geometrie, Math. Ann. 102(1930), no. 1, 337--362.
[31] Weil A., Foundations of algebraic geometry, American Mathematical Society, Providence, R. I. 1962.
[32] Yvonne, D. S., Interview with Bartel Leendert van der Aaerden, Notice of the AMS, Vol.44, No.3 (1997), 313--321.
本文来自微信公众号:返朴 (ID:fanpu2019),作者:段海豹(中国科学院数学与系统科学研究院研究员)、赵学志(首都师范大学数学科学学院教授),出品:科普中国

