最近,2011年诺贝尔奖得主里斯(Adam Riess,1969~)的团队宣布[1]:韦布空间望远镜(JWST)的观测证实,使用“距离阶梯法”得到的哈勃常数(Hubble constant)确实与宇宙学标准模型得到的哈勃常数不一致。两种方法得到的哈勃常数不一致,被称为 “Hubble tension”,可以被翻译为“哈勃冲突”。
那么,什么是哈勃常数?如何测量哈勃常数?“哈勃冲突”是如何产生的?如果确实存在“哈勃冲突”,那将意味着什么?
哈勃常数
1929年,哈勃(Edwin Hubble,1889~1953)测定了24个星系的距离,并与斯里弗(Vesto Slipher,1875~1969)此前测出的其中20个星系的速度,以及赫马逊(Milton Humason,1891~1972,哈勃当时的助手)测出的另4个星系的速度进行对比。

手持星系照片的哈勃。图片来源:公共版权
哈勃发现星系的退行速度与其距离成正比,这就是“哈勃定律”[2]。哈勃得到的结果让人们意识到宇宙在膨胀。[注1]
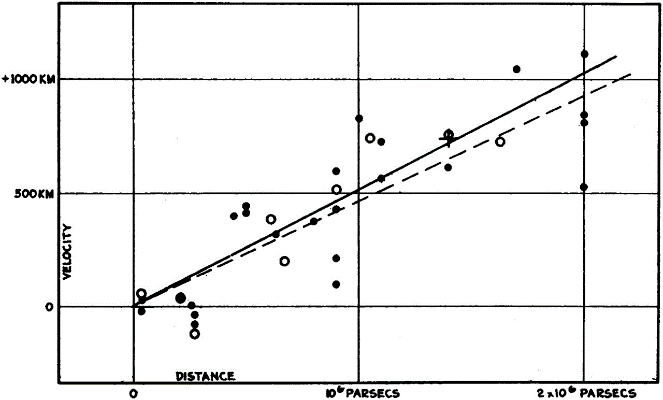
哈勃得到的星系的速度-距离图,二者基本上成正比。图片来源:参考文献[2]。
以km·s-1为速度单位,以兆秒差距(Mpc,即326万光年)为距离单位,将速度除以距离,得到的比例常数后来被称为“哈勃常数”,用符号“H”表示。哈勃当时算出的哈勃常数大约为550,其物理意义是:距离我们326万光年的一个物体(比如星系)以550 km s-1的速度远离我们。而更远的宇宙中的物体,以更大的速度远离我们。因此,哈勃常数被用以描述宇宙膨胀的快慢。
哈勃常数本质上是“速度除以距离”。那么它的倒数就是“距离除以速度”,即时间。因此,哈勃常数还与宇宙年龄密切相关:假设宇宙匀速膨胀,哈勃常数的倒数——“哈勃时间”——等于宇宙年龄(由于宇宙并不是匀速地膨胀,因此二者之间有差异;但巧的是,二者差异不大,都是约140亿年)。
哈勃常数H并不是真的常数,因为它在宇宙不同年龄时不同。我们后面所讨论的哈勃常数都是根据各种方法推出的“当前的哈勃常数”,用H0表示。
如何计算哈勃常数:距离阶梯法
早期的天文学家使用视差法测量天体的距离。视差法的基本原理是:在不同地方观测同一个天体,得到两条视线后,测出两条视线的夹角,再结合测量地点之间的距离,用三角函数计算出天体距离。夹角的一半被称为“视差”。[注2]
由于天体很远,视差的常用单位是角秒(更远得多的可以用毫角秒甚至微角秒),因此衍生出一个距离单位——秒差距。以地球与太阳的平均距离为基线,如果一个恒星的视差为1角秒,其距离就是1秒差距。1秒差距约等于3.262光年。在光速被确定之前,秒差距是恒星距离的标准单位。[注3]
然而,绝大部分恒星太远,视差小到无法测量。在地面上一般只能测出几百光年以内的恒星的视差。对于更远的距离,天文学家需要使用更强大的工具。1912年,哈佛天文台默默无闻的女天文学家勒维特(Henrietta Leavitt,1868~1921)根据持续的观测,发现一个重要规律:造父变星(Cepheid Variables)光度越高,变化周期越大。更精确地说,二者取对数后存在一次函数关系。[3]这就是著名的 “周期-光度关系”(“周光关系”),近些年也被称为“勒维特关系”。
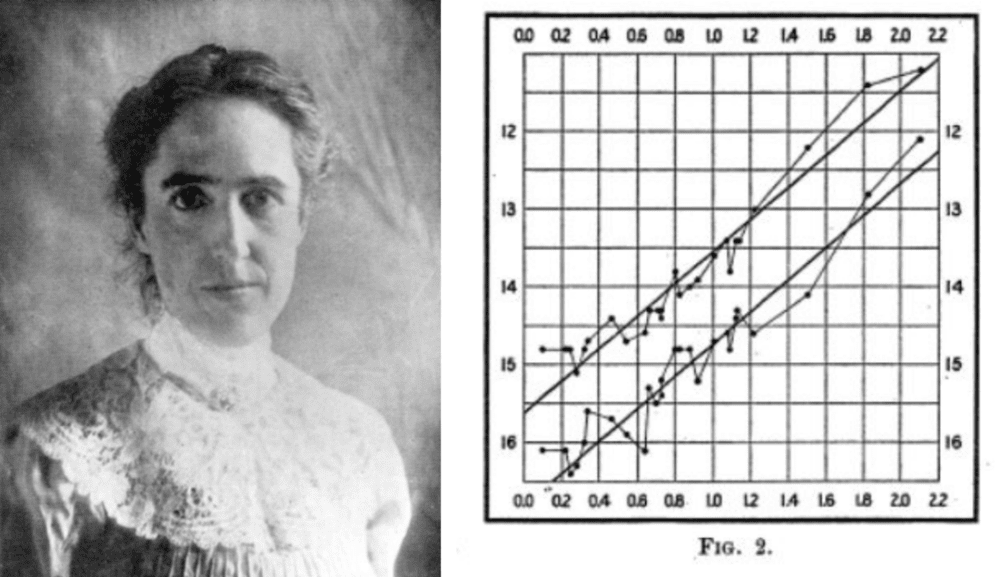
伟大而长期默默无闻的勒维特与她得到的周光关系。上下两组点分别代表不同造父变星的最大光度与最小光度,它们都满足简单的一次函数关系(见上下两条线段)。图片来源:公共版权(左);参考文献[3](右)
造父变星的周期是容易测出的,因此,只要用视差法测出近距离的造父变星的距离(从而得到其光度),就能以它们作为标尺,结合周光关系得到远距离造父变星的光度(从而得到距离)。
1929年,哈勃正是使用造父变星测出了那24个星系的距离。此后至今,造父变星成为天体测距中至关重要的一种“量天尺”。
造父变星法可以确定出的最远距离为1亿光年左右。更远的距离要用Ia型超新星来测定。尽管不同的Ia型超新星的最高光度存在差异,但一些人为“修正”方法可以将Ia型超新星改造为“标准化烛光”。如果在某个产生Ia型超新星的近距离星系内确认出造父变星,我们就可以通过测定造父变星的距离,来测出这些Ia型超新星的距离;然后根据“标准化烛光”,测出远距离的Ia型超新星及其所在的星系(“宿主星系”)的距离。
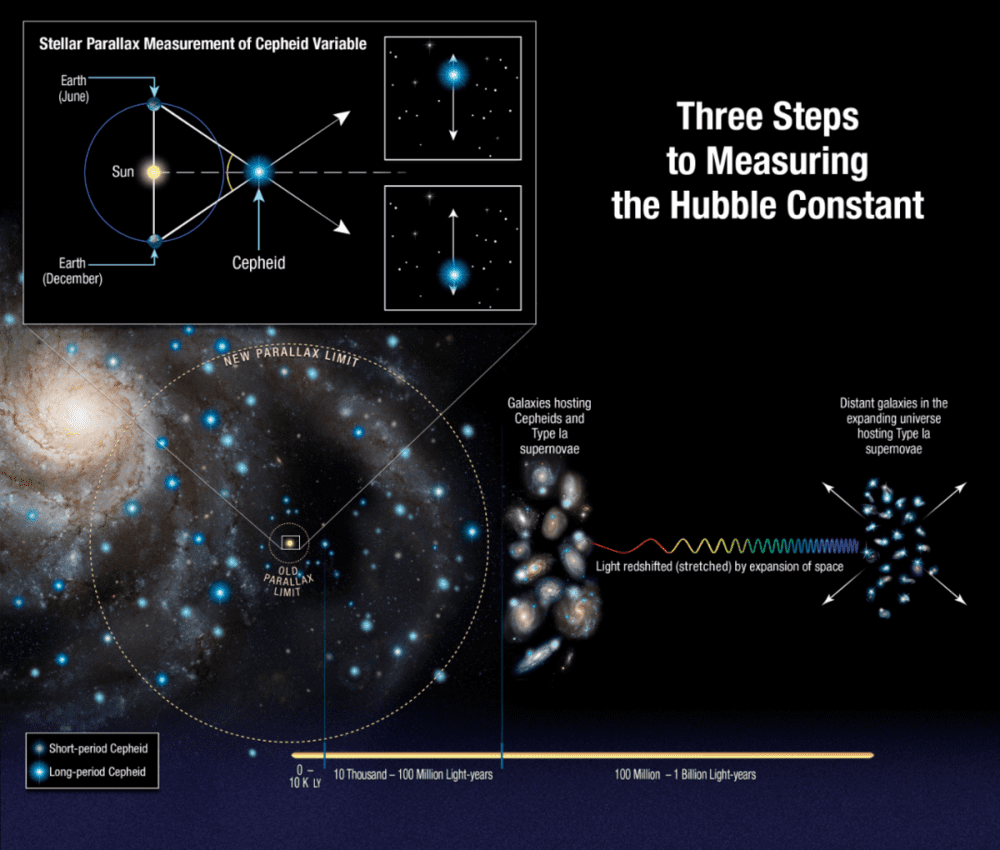
测量宇宙距离的三种方法:视差法、造父变星法与Ia型超新星法。对于更远的距离,用造父变星测距,再远的就用Ia型超新星来测距。图中虚线小圆表示单纯的视差法(旧方法)能够测出的距离极限,虚线大圆表示结合了造父变星法之后的视差法(新方法)能够测出的距离极限。小蓝点表示短周期造父变星,大蓝点表示长周期造父变星。图片来源:NASA, ESA, A. Feild (STScI), and A. Riess (STScI/JHU)https://esahubble.org/images/opo1812a/
这样就形成了一个三级阶梯:视差—造父变星—Ia型超新星。虽然这只是众多距离阶梯中的一种,但这个阶梯是最强大、最精准的距离阶梯。
哈勃当时混淆了两种造父变星,因此得到的哈勃常数偏大。后来经过不断修正,这个值在1990年之前被确定为50~100之间,但不确定性较大。1990年升空的哈勃空间望远镜(以下简称HST)可以测量到大约1万光年的距离。这使得精确测定哈勃常数成为可能。
天文学家执行了“哈勃空间望远镜关键计划”(KP)——通过对造父变星距离的精确测定来计算哈勃常数精确值。2001年,KP得到哈勃常数的值为72,误差为8。2011年,里斯领衔的团队根据对9个星系中造父变星的距离测量,计算得到哈勃常数的新数值为73.8,误差范围为2.4。这9个星系中,有8个星系曾经被观测到Ia型超新星爆发。
2013年,盖亚(Gaia)卫星升空,它可以测量到大约几万光年的距离。里斯等人执行了“超新星H0状态方程”(for Supernova H0 for the Equation of State)项目,简称“SH0ES”(酷似“鞋子”的英文SHOES)[4]。“SH0ES”结合HST与盖亚的观测,对距离阶梯的每一级进行更精确(即误差更小)的测定。
2022年,里斯等人根据SH0ES项目的观测,得到哈勃常数为73,误差为1。
标准宇宙学模型法
计算哈勃常数的另一种方法是使用标准宇宙学模型。该模型假定宇宙中的物质由暗能量、冷暗物质与普通物质构成。其中,暗能量用希腊字母Λ表示,冷暗物质的缩写为CDM;因此,标准宇宙学模型也被简称为ΛCDM模型。
使用标准宇宙学模型拟合宇宙微波背景辐射(cosmic microwave background,CMB)数据,就可以得到哈勃常数与其他重要的宇宙学参数。理论表明,CMB形成于宇宙大爆炸后约38万年,当时宇宙中的电子与氢离子(质子)复合为中性的氢原子,基本不再与光子相互作用。
这些光子因此“脱耦”,成为背景光子,当时它们的温度约为3000 K。随着宇宙不断膨胀,背景光子的波长被拉长约1000倍,能量也因此降低约1000倍,温度变为约2.725 K,主要集中于微波波段,因此得名宇宙微波背景辐射。
CMB反应了宇宙婴儿时期的面貌,蕴含着早期宇宙的极重要信息。宇宙学家们用宇宙学模型(ΛCDM模型)拟合CMB数据时,需要用到物质(包括普通物质与冷暗物质)含量、暗能量含量、哈勃常数、宇宙曲率(衡量弯曲程度)等参数。通过拟合,就可以得到这些参数的最佳值、中值与误差。
探测微波背景辐射的卫星先后有宇宙背景探测器(Cosmic Background Explorer,COBE)、威尔金森微波各向异性探测器(Wilkinson Microwave Anisotropy Probe,WMAP)卫星与普朗克(Planck)卫星。
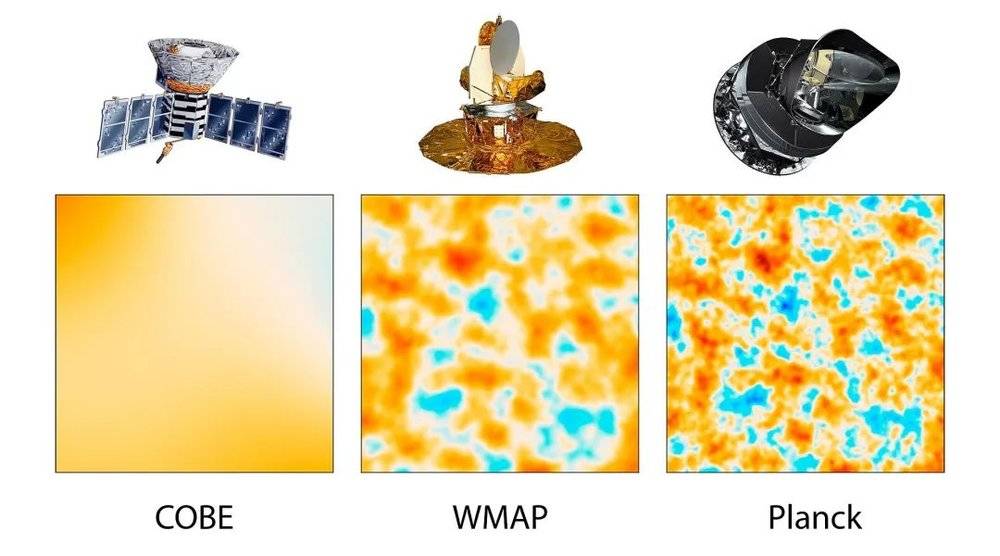
上方从左到右分别为COBE、WMAP与普朗克卫星的艺术想象图。下方分别是根据它们探测到的CMB数据绘制的伪色图。可以看到,WMAP的数据显示了比COBE更多的细节,而普朗克得到的数据比WMAP的数据更精细。图片来源:NASA/JPL-Caltech/ESA
根据早期的WMAP数据,宇宙学家得到的哈勃常数约为72,误差较大。从2003年开始,从WMAP的数据中拟合出哈勃常数的精度不断提高。普朗克卫星比WMAP更先进,根据它得到的数值拟合出的哈勃常数比由WMAP的数据得到的数值更准确,误差也更小。
2020年,普朗克卫星给出的哈勃常数为67.4,误差为0.5。[5]
两种方法的矛盾
于是问题出现了,即使都考虑误差,距离阶梯法得到的哈勃常数超过72,而ΛCDM模型得到的哈勃常数则低于68。如果只考虑中值,那二者的差异更明显,由前者推断出的宇宙膨胀速度比后者的推断大9%。
这就是文章开头提到的 “Hubble tension”(哈勃冲突)。
下图给出了不同年份(横坐标),用两种主流方法测出的哈勃常数值。使用距离阶梯法(KP、SH0ES、CPH、HST+Gaia2、HST+Gaia)得到的哈勃常数及其误差范围用蓝色点与误差棒表示;使用CMB数据(W1、W3、W5、W7、W9、P13、P15、P18、P+S4)得到的哈勃常数及其误差范围用红色点与误差棒表示。图中绿色表示根据双中子星(BNS)合并后产生的引力波测出的哈勃常数。
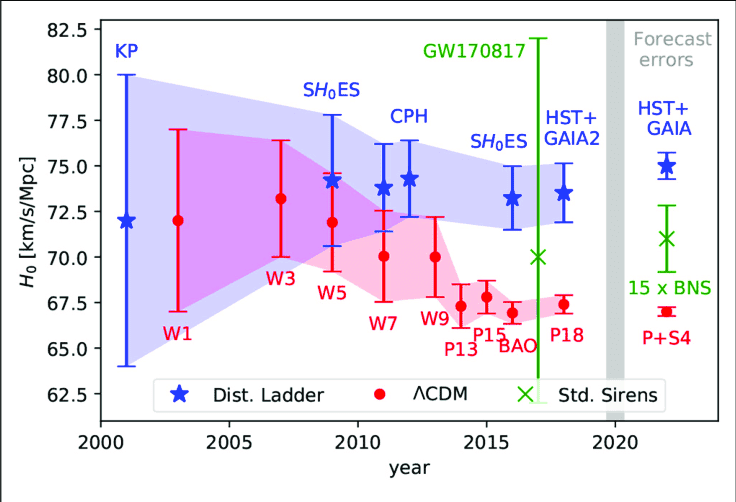
“哈勃冲突” (Hubble-tension) :随着精确度的提高,两种主流方法得到的哈勃常数的值开始出现明显差异。图中的KP代表哈勃关键计划;W代表WMAP,其后数字代表使用其年数的数据;P代表普朗克卫星。BNS现在误差较大,将来测出15个这样的事件后,就可能将误差大大减小。图片来源:https://www.researchgate.net/figure/The-Hubble-tension-adapted-from-Beaton-et-al-2016-Freedman-2017-including-the_fig6_329836950
可以看出,早期两种方法得到的数值存在重叠部分,没有矛盾。而到了后期,随着两种方法的误差都迅速减小,两种方法得到的数值不再重叠,出现明显差异。
JWST的红外观测:惊喜还是惊吓?
针对两种方法之间不可调和的矛盾,有人认为,随着距离的增加,造父变星的光与其周围恒星的光越来越难分开,因此受到附近恒星的光的污染越来越严重,导致HST在测定造父变星的光度时产生较大偏差;如果没有这种偏差,可能就没有哈勃冲突。
2023年,里斯团队使用JWST对5个星系进行了观测,它们都曾经爆发过Ia型超新星,且包含大量造父变星。他们从这些星系中确定出1000多颗造父变星。[5]
这次测量为宇宙学家们带来了一个好消息与一个坏消息。好消息是:JWST的红外观测品质比HST的红外观测品质更好;坏消息是:哈勃冲突没解决,而且以后没法甩锅给HST了。
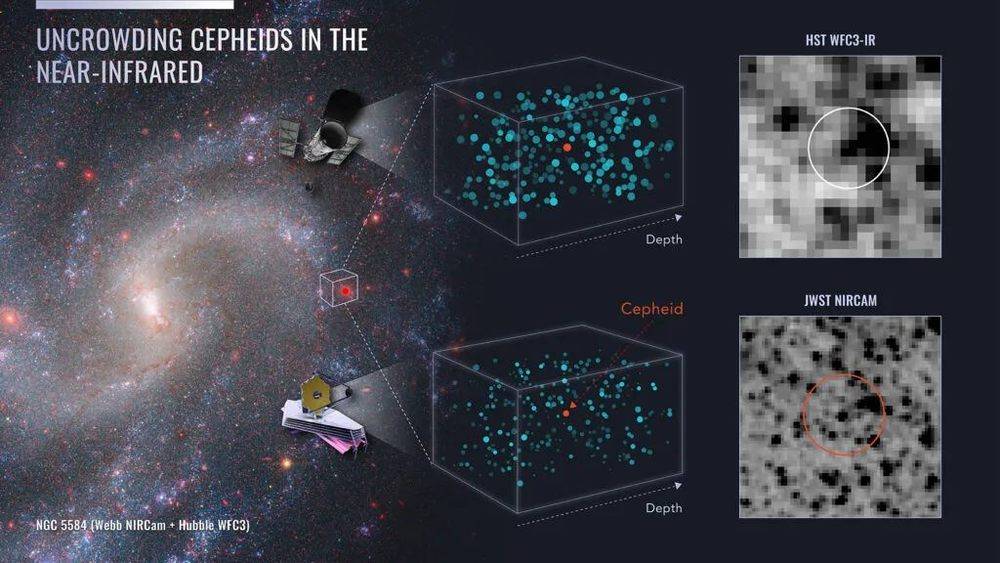
图中左侧为HST的第3代宽场相机(Wide Field Camera 3,WFC3)与JWST的近红外相机(NIRCam)的观测数据合成NGC 5584的图像。中间青色星群为二者观测区域中的恒星,红色点表示混在其中的造父变星。右上小图是HST的WFC3合成的图像,右下小图是JWST的NIRCam合成的图像。JWST更清晰的红外视野可以让作为目标的造父变星更明显地与周围的恒星隔离开来。图片来源:NASA, ESA, A. Riess (STScI), W. Yuan (STScI)
由于JWST的口径比HST更大,其分辨率比HST更高,能够清晰地将HST无法分辨出的众多光点分辨出来,使测光更精确。因此,JWST测出的造父变星的误差比HST得到的误差更小。
JWST的更精确观测表明此前的HST的观测虽然有较大误差,但并没有偏差,因为它测出的数值的中值与JWST得到的中值是几乎一致的,因此HST此前的观测是准确的[5]。哈勃冲突依然存在。
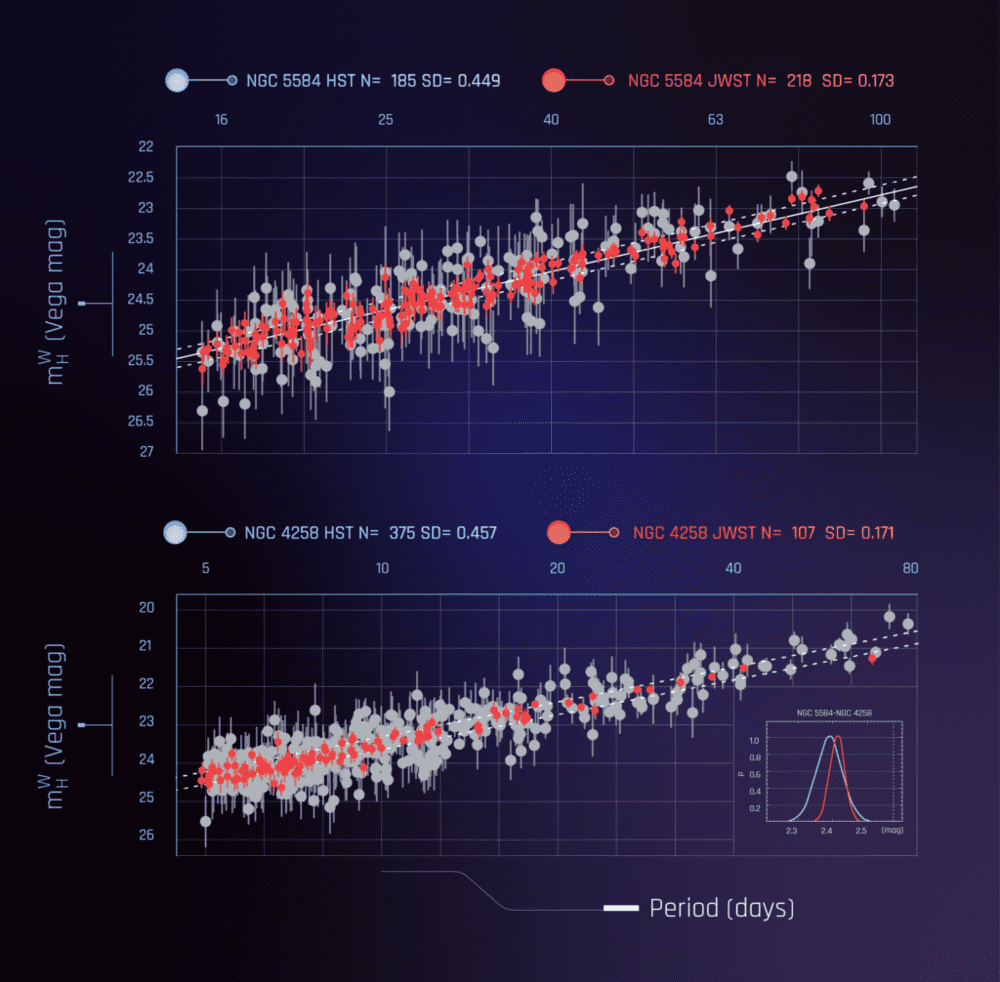
不同的造父变星的周期(横坐标)与亮度(纵坐标,用星等表示)关系。红点来自JWST,灰点来自HST。上图是Ia型超新星的宿主星系NGC 5584。下图是已知几何距离的星系NGC 4258。JWST的观测误差明显小于HST的观测误差。由于每张图中的造父变星分别来自同一个星系,因此同一张图中的造父变星与地球的距离相同,亮度差异也就衡量了光度差异。图片来源:NASA, ESA, A. Riess (STScI), and G. Anand (STScI)
如果距离阶梯法对哈勃常数的测量确实准确,那ΛCDM模型中的其他参数必须改变,这样才可以让这个模型拟合出的哈勃常数等于距离阶梯法得到的值。这里的“其他参数”涉及暗能量、暗物质、宇宙曲率,等等。
因此,要想解决这个问题,可能要假设有奇特的暗能量,或奇特的暗物质,或新的相对论性粒子(如奇特的中微子),或者假设宇宙的曲率与零有轻微偏离(即宇宙是轻微弯曲的)。如果这些假设中的任何一个成立,就意味着基础物理学又要发生新的变革。[4]
如果是距离阶梯法出了问题,那就意味着我们必须检查修正与恒星天文学有关的一些知识了。因此,哈勃冲突对于天文学与宇宙学都是一个挑战。
“真是个天才”
最后再谈谈“Hubble tension”(哈勃冲突)这个词组。它既描述了使用两大类方法得到的“哈勃常数”之间的冲突(tension),其读音又与英文中“高血压”(hypertension)这个词相近。
我特意查找了Di Valentino等人[6]于2021年发表的长达110页的关于“哈勃冲突”的综述论文,但没有发现里面提到哪篇文献最早提出“Hubble tension”这个词组,虽然里面出现了近300次“Hubble tension”。
所以我暂时还不知道谁发明了这个词组。不过,不管发明“哈勃冲突”这个词组的人是谁,也不管此人有没有高血压,哈勃冲突倒是真会让一部分有高血压的宇宙学家因为血压升高而头疼。
套用一个网络热梗来说:发明“Hubble tension”这个词组的人真是个天才。
注释:
[注1] 勒梅特(Georges Lemaître,1894-1966)结合星系退行的事实,在1927年通过广义相对论证明宇宙在膨胀,星系的退行速度与距离成正比。2018年,国际天文学联合会第30届大会将“哈勃定律”改称为“哈勃-勒梅特定律”。后来,“哈勃常数”也被称为“哈勃-勒梅特常数”。为了行文简洁,我们依然称之为“哈勃常数”。实际上,勒梅特不仅用到了斯里弗得到的速度数据,也用到哈勃此前测出的星系数据(但数据质量比较差),因此得到了一个很粗糙的正比关系。
[注2]必须注意的是,大多数展示视差法的示意图只显示了两次测量;事实上,这种方法需要多次测定,才可以得到可靠的距离数值。
[注3]即使到现在,绝大多数天文学术论文与学术著作中依然只使用秒差距(以及千秒差距、兆秒差距等更大的单位)作为距离单位。
参考文献:
[1] Riess, A. G., Anand, G. S., Yuan, W., et al. 2024, ApJL, 962, L17. doi:10.3847/2041-8213/ad1ddd
[2] Hubble, E. 1929, Proceedings of the National Academy of Science, 15, 168. doi:10.1073/pnas.15.3.168
[3] Leavitt, H. S. & Pickering, E. C. 1912, Harvard College Observatory Circular, 173
[4] Riess, A. 2023, American Astronomical Society Meeting #241, id. 424.01. Bulletin of the American Astronomical Society, Vol. 55, No. 2 e-id 2023n2i424p01
(https://ui.adsabs.harvard.edu/abs/2023AAS...24142401R/abstract)
[5] Planck Collaboration, Aghanim, N., Akrami, Y., et al.\ 2020, \aap, 641, A6. doi:10.1051/0004-6361/201833910
[6] Di Valentino, E., Mena, O., Pan, S., et al. 2021, Classical and Quantum Gravity, 38, 153001. doi:10.1088/1361-6382/ac086d
本文来自微信公众号:返朴 (ID:fanpu2019),作者:王善钦,本文受科普中国·星空计划项目扶持,出品:中国科协科普部,监制:中国科学技术出版社有限公司、北京中科星河文化传媒有限公司

