光看标题,读者可能以为杨大卫是一位华人学者。其实他是纯粹的美国人,全名为David M. Young Jr. (1923年10月20日-2008年12月21日)。他不像德国“大卫”——David Hilbert(1862-1943)那样蜚声国际数学界,我甚至查不到他全名的标准中文翻译;再加上他的姓在西方人中罕见地只有一个元音,我就顺势给他起了个响亮的中文名字:“杨大卫”。
杨大卫生前在计算数学界是个响当当的人物。他毕生致力于求解线性方程组的迭代法,最伟大的成就是发明了SOR方法,即逐次超松弛迭代法(successive over-relaxation method)。更了不起的是,这项与时俱进的发明脱胎于他在1950年完成的博士论文。
按照抽象代数名家和教学名师丁石孙(1927-2019)校长所言,数学博士论文“有百分之九十大几的比例对所在学科没有影响”。但是,杨大卫的博士论文影响了整个线性迭代法。1984年,我在南京大学读到了丁校长的采访记录,感受到他希望研究生们多读书以拓宽知识面,而不囿于一篇学位论文的苦心。
杨大卫于1944年在纽约州的韦伯海军建筑学院获得学士学位,为海军工作到二战结束,其后进入哈佛大学数学系读研究生,分别于1947年和1950年获得硕士和博士学位。他的博士论文导师是加勒特·伯克霍夫(Garrett Birkhoff,1911-1996)。加勒特和父亲乔治(George David Birkhoff,1884-1944)是少见的数学家父子,而且都是哈佛教授,父亲在动力系统和遍历理论领域有开创性贡献,儿子的成就主要集中在格论(lattice theory)。
格论是抽象代数的一个分支,起始于布尔代数,研究的对象是有序集,小伯克霍夫在老伯克霍夫任教的哈佛大学数学系本科毕业后,去了剑桥大学,先学数学物理,后转向抽象代数。在游学欧洲的那年,他从几大数学名家那里获益良多。
1933年后,他一直待在哈佛。期间发表的一系列论文,构成了他1940年出版的经典著作《格论》,其第三版至今还在印刷。二战中,他的兴趣转向应用数学,尤其是流体力学,研究成果包含在他于1950年出版的专著《流体动力学》中。由于和冯·诺伊曼是好朋友,他在三十五岁后对计算的爱好与日俱增。
这就是1948年杨大卫投入伯克霍夫教授门下攻读博士时的背景。导师给了弟子一个题目:研究数值求解泊松偏微分方程。正是对这一博士学位论题的研究推动了SOR方法的问世。之后若干年,在杨大卫研究工作的基础上,伯克霍夫与1950年进入哈佛数学系读研究生的瓦尔加(Richard Steven Varga,1928-2022)合作,研究了用于微分方程和正算子的迭代法。瓦尔加于1962年出版的《矩阵迭代分析》成了这一领域的经典著作。
杨大卫在他1990年撰写的综述性文章《迭代方法的历史回顾》( A historical review of iterative methods)中回忆,当他找伯克霍夫教授选博士论文题目时,心中的头选是纯数学领域的李代数,但是教授建议他做计算数学的“松弛方法”,并递给他几篇文献,其中包括论文《拉普拉斯和泊松方程的数值解》( Numerical solution of Laplace’s and Poisson’s equations)和英国数学家索斯韦尔爵士 (Sir Richard V. Southwell,1888-1970) 的著作《理论物理中的松弛方法》( Relaxation Methods in Theoretical Physics)。
所谓“松弛方法”,从广义上讲是指获得偏微分方程近似数值解的过程,但从狭义上讲,它仅指用于求解线性代数方程组Ax = b的迭代过程。在此过程中,“松弛”技术与方程组的残量r = b - Ax密切相关,目的是加快收敛。
伯克霍夫对杨大卫的博士论文研究帮助很大,他不仅提供了指导和鼓励、给出建议的参考文献,还仔细阅读了论文草稿。据杨大卫回忆, “逐次超松弛方法”的英文全称就是伯克霍夫建议的——“我相信这是一个很好的选择”。这样的导师堪称良师益友。
杨大卫的博士论文研究开局并不顺利,甚至来访的索斯韦尔爵士也留下一句令人沮丧的评述“任何机械化松弛方法的尝试都是浪费时间( Any attempt to mechanize relaxation methods would be a waste of time)。”但他毫不气馁,继续工作。不久他有了一个好发现:对某些线性方程组,高斯-赛德尔迭代矩阵的特征值是雅可比迭代矩阵特征值的平方。
得益于从阅读相关文章获得的灵感,杨大卫有了突破性的进展:对于他通过引进超松弛因子ω而设计出的SOR方法,如果方程组系数矩阵A一致有序 (consistently ordered),则其迭代矩阵的特征值与雅可比方法迭代矩阵的特征值有个关键性的关系。他所数值求解的椭圆型偏微分方程在区域网格按从左到右和向上的自然顺序编号,使用标准五点差分格式,会产生一致有序的矩阵。
我在之前一篇《返朴》文章《简单实用!3个德国人创造的线性迭代法,超越了一个时代》中介绍了雅可比迭代法和高斯-赛德尔迭代法,在此基础上,可以进一步了解杨大卫的SOR方法。设Ax = b为待解的线性方程组,其中n阶系数矩阵A为非奇异的,b为给定的n维列向量,x为n维未知列向量。将A写成其严格下三角部分L、对角线部分D和严格上三角部分之和:A = L + D + U,则原方程可写为Lx = b – (D + U)x。
令ω为一个小于2的正数,称为松弛因子。上述方程等价于ωLx = ω[b – (D + U)x],两边加上Dx,得(D + ωL)x = Dx + ω[b – (D + U)x]。化简右端,便有
(D + ωL)x = ωb – [ωU +(ω - 1)D]x, (1)
这就是SOR方法的方程组形式。如果让ω = 1,(1)就变成(D + L)x = b – Ux,即高斯-赛德尔方程组。
为何在经典高斯-赛德尔方法的矩阵形式中塞进可调参数ω?这是为了改善收敛速率。SOR方法的迭代格式如下:
xk = (D + ωL)-1{ωb – [ωU + (ω - 1)D]xk-1, k = 1, 2, …。
利用方程(1),容易写出上述向量迭代的分量形式:
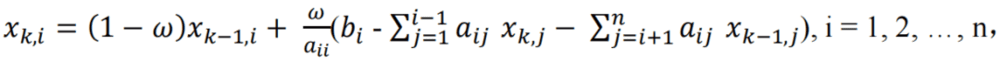
其中xk,1, …, xk,n为xk的n个分量。
如果将SOR迭代格式写成线性迭代法的标准形式,则
xk = Mωxk-1 + c, k = 1, 2, …; Mω = -(D + ωL)-1[ωU + (ω - 1)D], c = ω(D + ωL)-1b。
我们知道SOR方法收敛的充分必要条件是其迭代矩阵Mω的谱半径ρ(Mω) < 1,而且这个数越接近0,可能的收敛速率就越快。由于谱半径不仅是ω的函数,也依赖于矩阵A的种类,因此如何选取参数ω,使得谱半径可能达到最小,就成为最优收敛性分析的中心。
正如杨大卫在他博士论文中得到的,当A是一致有序时,Mω的任一特征值λ和雅可比迭代矩阵M1 = I – D-1A的一个特征值μ满足如下关系
(λ + ω -1)2 = λω2μ2。
如果A是对称正定的,则M1的特征值都为实数,且绝对值小于1。这时SOR方法的最佳因子为
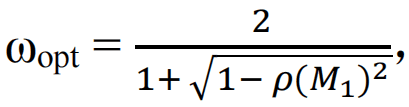
其对应的SOR方法迭代矩阵的谱半径为
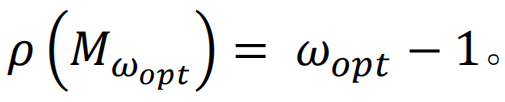
上世纪四十年代末,杨大卫研究迭代方法伊始,对于在新生的电子计算机上使用迭代法求解大型问题的想法,有人表示怀疑。但自从他开创性的博士论文问世后,迭代法已被广泛应用于科学和工程中,并衍生出许多新的变种。
在科学计算的广阔领域,杨大卫的功绩永远不会被人遗忘,今年12月21日是他十五周年忌辰,谨以此短文感谢他,并简单介绍他留名数学史的博士论文成果——SOR方法。
本文受科普中国·星空计划项目扶持
出品:中国科协科普部
监制:中国科学技术出版社有限公司、北京中科星河文化传媒有限公司
本文来自微信公众号:返朴 (ID:fanpu2019),作者:丁玖(美国南密西西比大学数学系教授)

