渴望假期是人类的共性,和教育背景、所学专业等无关。科罗拉多大学博尔德分校数学系研一学生Summer Haag,还有与她同系的Clyde Kertzer,早在今年5月就开始憧憬着这个暑假。Kertzer还在上本科,他计划在暑假里好好踢上几场足球,然后精心准备自己的研究生入读申请。Haag则期盼着在假期里放松一下身心,重新拾起自己最热爱的登山运动。
但是,当他们听说自己的导师、数论专家Katherine Stange发布了一个半日制暑期研究计划之后,经过一番内心纠结,最终数学研究的热情还是压过了对于休假的渴望,他们两人选择申请加入其中。
Stange对“看似简单但结构丰富的问题”很感兴趣。她的团队这一次所瞄准的数学对象,是数学史上最古老的几何结构之一。Stange常见的研究风格则是,通过计算机生成大型数据集来解决数论里难以捉摸的开放问题。作为项目组里最年轻的两位成员,Haag和Kertzer主要负责相对简单的“体力劳动”——扩展组内数学家James Rickards的算法和初始代码,编写程序,生成大量模拟数据,最终以可视化的形式展示当数学结构进一步趋于复杂时的数值发展趋势。
出乎所有人的意料,Haag和Kertzer加入项目组还未满一个月,他们的劳动成果就打了整个数论领域一个措手不及。大量数据暗示,Stange团队原本打算证明的那个猜想,实际上是错的。在此之前,该领域的学者几乎都相信它是正确的,唯一的问题在于如何证明它。
这个猜想发轫于最古老的尺规作图问题,在文艺复兴时期经由笛卡尔的美妙定理初见端倪,中间又有诺贝尔化学奖得主提供的洞察力,现在则跨进了最前沿的数论领域……它的来龙去脉,就如同一条经纬,贯穿了一部微缩的数学史。而始发站,正是两千多年前的古希腊。
一、古希腊:阿波罗尼奥斯的相切圆
2200年前出生于小亚细亚佩尔加(今属土耳其)的阿波罗尼奥斯(Apollonius of Perga)是欧几里得之后,古希腊几何学的第二位集大成者。由他所撰写的8卷《圆锥曲线论》(Conics)是数学史上真正的经典巨著,代表了希腊几何的最高成就。
不过,我们下面要谈到的是他的另一部作品《论相切》(On contacts或Tangencies)。
尽管原本的《论相切》已失传,但通过后来几代数学家的引用和注释,我们仍然能够了解一些其中的内容。其中最为重要的记录来自大约500年后的《数学汇编》(Synagoge)一书,它由被誉为亚历山大学派“最后一位伟大的几何学学者”的帕普斯(Pappus)整理完成。
阿波罗尼奥斯被认为是古代伟大的数学家之一。他的著作(这里看到的是 9 世纪的阿拉伯语译本)继续发展了约一个世纪前欧几里得的几何思想。| 图源:Bodleian Libraries/Oxford University
阿波罗尼奥斯在《论相切》里提出了一个几何学难题:在平面上给出位置关系没有特别限制的三个圆,问如何用尺规作出第四个圆与之前的三个圆相切?此即著名的阿波罗尼奥斯问题(Apollonius’ problem)。
阿波罗尼奥斯找到了作图方法,指出对于最一般的情况,一共有8个可能的解。
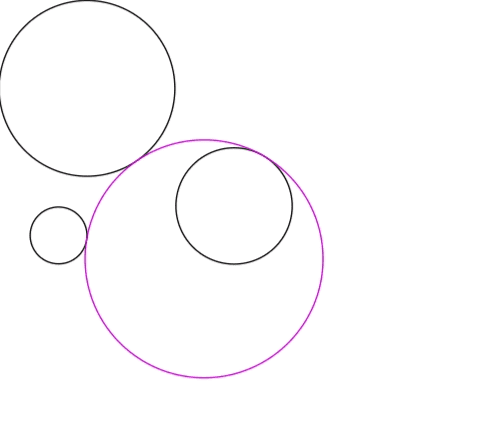
上图显示了8个解中的1个:对一般位置的三个黑色圆,紫色圆包含其中一个并与它们全部相切。紫色圆可以包含一个圆,也可以包含两个圆,以及同时包含所有圆或不包含任何圆,但都与全体相切。| 图源:wiki Apollonian gasket
显而易见,对于位置相对特殊的三圆配置,可与其全部相切的第四个圆,很可能不足8种。例如,若限定三个圆两两相切,则第四个圆仅有2种可能性。
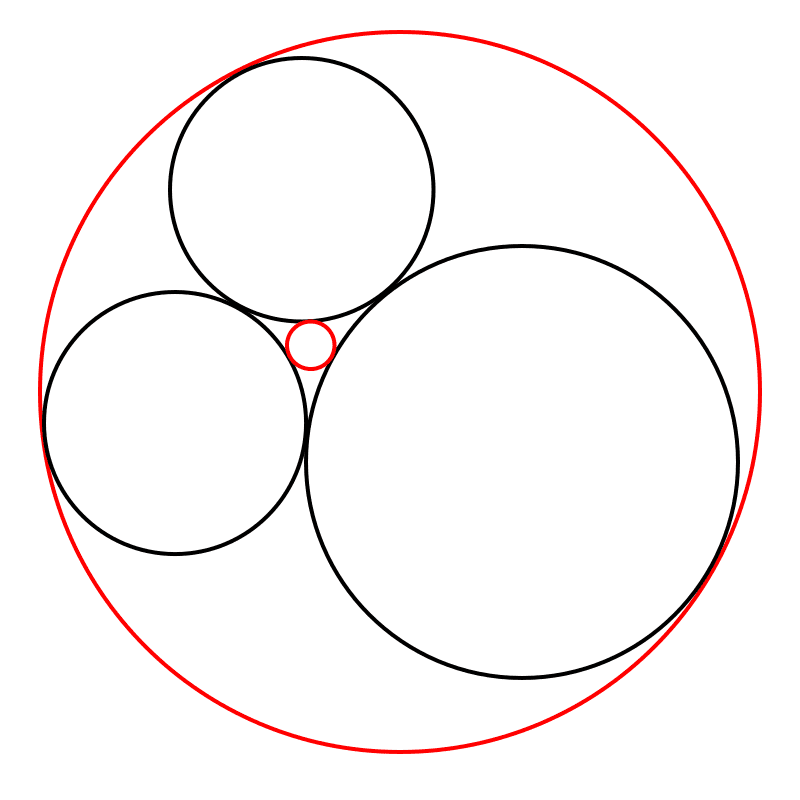
如上图,当三个黑圆彼此外切时,与它们同时相切的红圆要么把三个黑圆包含在内,要么位于三个圆之间的区域。| 图源:https://en.wikipedia.org/wiki/Descartes%27_theorem
如果我们选择包住三个小圆的大圆,则可以继续用尺规作图实现如下的操作:在大圆内部作出一个圆,使其与平面上已经存在(作出)的三个圆相切。显然该过程可以无限持续下去,用越来越小的圆,填充圆与圆之间的空隙。效果如下图:
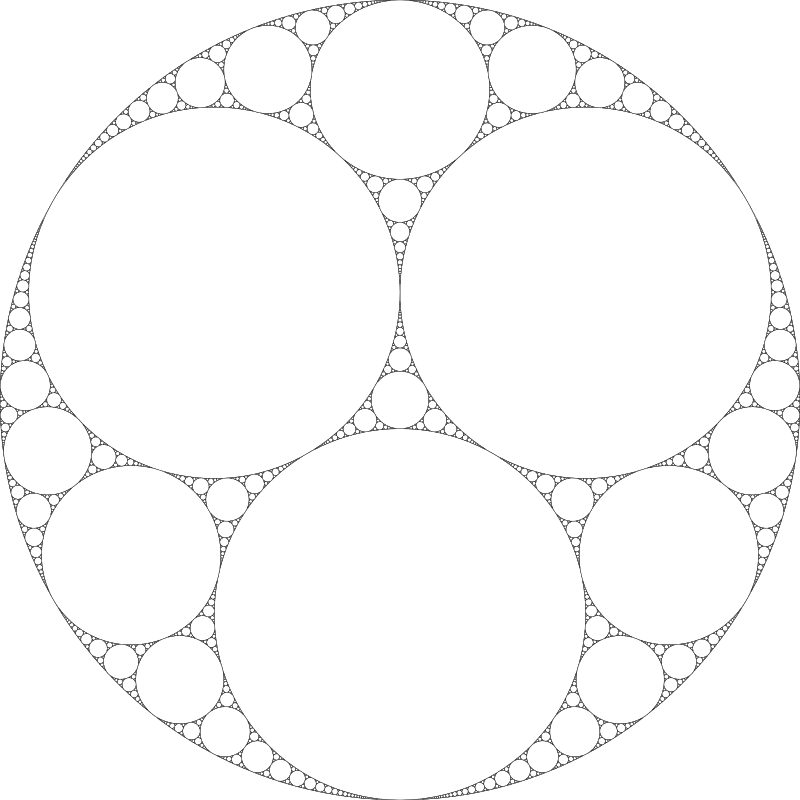
图源:Apollonian gasket - Wikipedia
由于这些大大小小的圆盘就像是一个个密封垫,上图里的几何结构被命名为阿波罗尼奥斯垫圆(Apollonian gasket)。这便是本文的“主角”。
在解决问题的过程中,阿波罗尼奥斯似乎使用了一个看似显而易见的结论:在切点不重合的情况下,平面上至多只能作出四个圆,使其任意两个圆均相切;或者说,无论如何调节半径大小和位置,都不存在五个圆,其中每个圆与另外四个圆相切。
但按照现代数学的公理化体系,“不存在五个圆,其中每个圆与另外四个圆相切”这一命题是可以证明,且应该予以证明的。此处便把它留作一个思考题。
二、文艺复兴:笛卡尔的美妙定理
直到文艺复兴时期,后世的数学家都企图利用帕普斯对《论相切》的概述,重现阿波罗尼奥斯的原始发现。然而,真正继承了阿波罗尼奥斯精神的是勒内·笛卡尔(René Descartes)。他引入了笛卡尔坐标系,通过在平面上引入坐标轴,将点与实数对应起来,从而将几何问题转化为代数问题。这一开创性的思想为后来的数学发展铺平了道路。
更妙的是,具体到阿波罗尼奥斯问题——仿佛是为了昭示其继往开来者的身份——恰也是笛卡尔本人,做出了阿波罗尼奥斯之后最为重要的发现:堪称“美轮美奂”的笛卡尔定理。
为了介绍这个美丽的定理,我们不可避免地要涉及到曲率的概念。曲率,简而言之,是描述曲线在不同位置上的弯曲程度的度量。
首先,想象一条直线。它没有弯曲,因此其曲率为零。接下来,考虑一个圆,不管圆上的哪个位置,它的弯曲程度都是一样的。圆的曲率似乎是一个常数。但是,当我们观察抛物线时,情况就变得更加有趣。抛物线的曲率在不同位置上是不同的,因为其弯曲程度不均匀。
我们还可以通过一种直观的物理图像来理解曲率:想象一个小车沿着曲线运动。当小车转弯时,它需要向中心点施加一个力,我们称之为向心力。这个向心力的大小取决于小车的速度和转弯时画出的圆弧半径。当转弯半径很小时,向心力会增大,这意味着曲线在该点的弯曲程度更高。
基于上述物理图像,我们可以如此定义曲率:对曲线上的某一点A,该点的曲率是与曲线相切于A点的最大的圆的半径的倒数。
需要注意的是,曲率定义中的相切圆必须是“最大的圆”。显而易见,曲率越大,曲线的弯曲程度越高。对于一个圆,其圆周上各点的曲率都是自身半径的倒数;对于直线,与之相切的圆的半径,想要多大就可以有多大,所以直线的曲率是无穷大的倒数,亦即为0。
有了曲率的概念,我们就可以表述笛卡尔在研究相切圆时的发现。这位大哲学家断言,只要四个圆彼此相切(切点不重合),则它们的曲率必然满足如下简单关系,
所有曲率的平方和等于曲率和的平方的一半。
如果四个彼此相切的圆的曲率分别为a、b、c、d,则上面的定理可用代数式表示成,2(a2+b2+c2+d2)=(a+b+c+d)2
笛卡尔定理的发现是数学上的一个里程碑,它代表了代数与几何的融合,以及代数工具在解决几何难题中的巧妙运用。从另一个角度来说,解析几何之父率先找到了相切圆的几何结构中的美妙代数关系,似乎也就顺理成章了。
此外,还需要两点额外的说明。
第一,在使用笛卡尔定理的时候,出于一些原因我们需要人为定义曲率的正负符号。若一个圆与另三个圆外切,则每个圆的曲率都是正数。但如下图里的大圆包含三个内切圆,则我们定义大圆的曲率为负数。如此一来,四个彼此相切的圆的曲率分别为a、b、c、d,如果a、b、c为已知,d的取值恰有正负两种情况。
第二,在上一节里我们提到过这个命题,“在切点不重合的情况下,平面上至多只能作出四个圆,使其任意两个圆均相切”。表述里“切点不重合”的这个条件是必要的,如下图,如果几个圆切于一点,则上一节的命题不成立,笛卡尔定理也不成立。
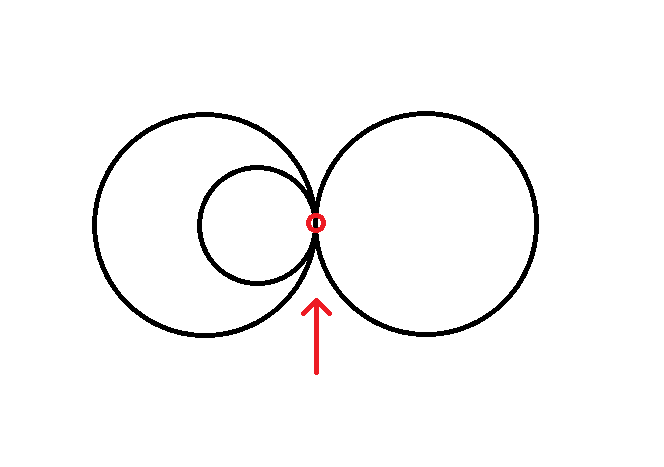
图源:https://en.wikipedia.org/wiki/Descartes%27_theorem
三、20世纪:诺贝尔化学奖得主的数学赞美诗
英国化学家弗雷德里克·索迪(Frederick Soddy FRS)在放射化学和原子物理学方面作出了重要贡献。他与欧内斯特·卢瑟福(Ernest Rutherford)共同解释了元素嬗变导致放射性的机制。他还证明了某些放射性元素同位素的存在性。1921 年,他被授予了诺贝尔化学奖,“以表彰他对放射性物质化学知识的贡献”。
索迪对数学也非常感兴趣,尤其是与圆或球相关的问题。
1936年,他独立发现了上一节里的笛卡尔定理。在进一步研究如何填充阿波罗尼奥斯圆的过程里,索迪立刻注意到一个在过去200多年里被数学家们所忽略的现象:当圆变得越来越小,曲率变得越来越大时,他期望得到一些带有平方根或无限小数的复杂数字。然而,如果最开始的三个相切圆的曲率是整数,则后来所有圆的曲率都是整数。这是笛卡尔定理一个相当直接的结果,但几百年来竟无人注意到。
激动之余,索迪诗兴大发,直接向《自然》(Nature)杂志上投稿了一首数学诗。他用诗歌的语言描述了笛卡尔定理的内容。
诗的标题是The Kiss Precise(精确的吻,意指相切),摘录若干翻译如下:
要让两对嘴唇相吻也许/不需要任何三角学。
但当四圆相吻时/每个都要同时吻另三个伙伴。
四个圆的曲率之和/等于它们的平方和的一半。
如果你想知道它们的大小/只需解出我的方程。
……
虽然它们向欧几里得保守住了秘密/现却无需以经验为据。
零曲率即变为直线/凹曲率应带有负号的标志,
待我再说一遍,所有四个曲率的平方之和/为其总和的平方的一半。
……
不过无论如何,索迪不仅展示了他对数学之美和诗歌艺术的热爱,也为后来的研究提供了一个重要的工具。
如果说,笛卡尔的定理,从古老的欧式几何学问题里,信手拈出了其最核心的代数关系;索迪的“捡漏”发现则指出,这种关系蕴藏了丰富的算术性质。
算术,即是数论。
四、启蒙与理性时代:高斯的钟表计数器与二次互反律
数论是基础数学里最古老但又很年轻的一个分支。
说它古老,早在欧几里得的《几何原本》里便收录并用反证法证明了最古老的数论命题:存在无限多个素数。
另外, 古希腊的丢番图(Diophantus)留下了一篇具有数学谜题性质的《丢番图墓志铭》,后者因此被誉为最著名的不定方程(指未知数只能使用整数的整系数多项式方程)。也正是因为这一渊源,不定方程也被称之为丢番图方程。
说数论年轻,则是因为在随后两千年的数学史里,虽然出现了费马、欧拉、勒让德(Adrien-Marie Legendre)等一大批推动了数论发展的巨人,但真正使这一数学分支严谨化和系统化的人,则是被誉为数学王子的卡尔·弗里德里希·高斯(Carl Friedrich Gauss)。
在高斯的《算术研究》第一章,他引入同余的概念。他是第一位把算术里最基础的语言,同时也是蕴藏着最深刻思想的工具——模运算——明确地“捻”出来的数学家。
为了方便后文的理解,这里简要介绍一下模运算。
在整数里,最基础的关系是整除性。对于整数m和n。如果存在另一个整数k,使m=k×n,则我们说n整除m。如2整除4,7整除56等等。
对于三个整数p、q、m,如果m整除p-q,则说p和q关于m同余。或者,用高斯的表示法,就是![]() (mod m)。
(mod m)。
因为28-1=27=3×9,所以![]() (mod 9);类似可知
(mod 9);类似可知![]() (mod 3)。
(mod 3)。
这里的mod 9,就是取模运算,高斯也将这种运算称之为钟表计数器。
我们用24小时制的时间表示法,若现在是7点整,问:100个小时后,时间是当天的几点?
用数论的语言重写上面的问题:若![]() (mod 24),其中小于24的x是多少?
(mod 24),其中小于24的x是多少?
7+100![]() 7+24*4+4
7+24*4+4![]() 7+4=11(mod 24),所以答案是11点。
7+4=11(mod 24),所以答案是11点。
有了取模运算的定义,我们还可以进一步把丢番图方程扩展到模运算上。
最简单的,比如说,是否存在整数x,满足x2![]() 1(mod 16)?而为了系统性地解答如下问题:是否存在整数x,满足x2
1(mod 16)?而为了系统性地解答如下问题:是否存在整数x,满足x2![]() a(mod p),其中p是一个素数?
a(mod p),其中p是一个素数?
高斯证明了名为二次互反律(quadratic reciprocity)的算术定理。私下里,高斯把二次互反律誉为算术理论中的宝石。它也被称为“数论之酿母”,在数论中处于极高的地位。
遗憾的是,二次互反律的内容相对复杂,不适合在本文中进行介绍。
五、现代:本科生的工作推翻了前沿数学里的著名猜想
掌握了模运算,也意味着我们终于来到了本次数学之旅的终点。
自从英国化学家索迪提供了颇具诗意的洞察——只要最开始的三个相切的圆的曲率是整数,则后来所有圆的曲率都是整数——数论学者就开始研究古老的几何构造的算术性质。
考虑笛卡尔定理的表达式:2(a2+b2+c2+d2)=(a+b+c+d)2,如果已知的三个数都是整数,则它显然变成了一个丢番图方程。
例如,现在有三个曲率分别为11、14和15的圆,你可以将这些数字代入由笛卡尔定理给出的方程,计算出能够填充进它们之间的圆的曲率:86。
数论专家非常有兴趣了解这个丢番图方程的解的信息。譬如说,连续在大圆里填充阿波罗尼奥斯垫圆,随着圆的半径越来越小,其曲率越来越大,相邻的四个圆之间,又被笛卡尔定理约束;此时曲率的整数值会呈现出什么样的规律?
2010年,Elena Fuchs,现在是加州大学戴维斯分校(University of California,Davis)的一位数论专家,证明了曲率遵循一种特定的关系。
如果把每个曲率的数值mod 24,则会出现一条规则。有些构造只有与0、1、4、9、12或16同余的曲率。其他一些仅留下余数为3、6、7、10、15、18、19或22的曲率。
不久之后,借助实际构造的有限模型,数学家们开始相信,如果某个阿波罗尼奥斯垫圆结构里存在一组曲率,其中曲率的数值彼此互素,且每一个都与一个已知的整数r同余 (mod 24),则除去有限的例外,这组曲率应包含了所有满足下述同余式的整数x:
x![]() r(mod 24)
r(mod 24)
这个想法被称为局部-全局猜想(local-global conjecture)。其实在数学里有很多以“局部-全局”命名的猜想,这里特指阿波罗尼奥斯垫圆上的局部—全局猜想。
回到本文的开头,科罗拉多大学博尔德分校数学系研一学生Summer Haag与大四的Clyde Kertzer舍弃假期,加入了自家导师的暑假研究项目。他们的导师Katherine Stange希望能够证明阿波罗尼奥斯垫圆上的局部—全局猜想。
她指派Haag和Kertzer编写程序,生成大量阿波罗尼奥斯垫圆,以找出数据中隐藏的规律。Haag用Python脚本制作了一些同时绘制大量模拟图表的程序。当Stange临时离开学校,前往欧洲参加一场学术会议的时候,Haag做了一个大动作。
Haag一直在绘制1000个整数是如何相互作用——数据比它听起来的要庞大,因为它涉及到100万对可能的数字。然后她把参数调到了10000乘10000。在生成的图表中,行和列里的黑点拒绝消失。它看起来一点也不像局部-全局猜想的预言结果。
等Stange从欧洲返回,在每周的碰头会上,Haag和Kertzer向项目组里的成员展示了带有反常数据的图表。他们两人承认,不知道是哪里出了bug。
他们的导师凝视着图表,突然说道:“如果是局部-全局猜想压根就不成立呢?”
“我当时很兴奋。很少有事情真正能让我们感到惊讶。”Stange后来说,“但这就是数据的魔力。”
一旦找准了方向,Stange的团队在几周内就得到了一篇严格证明,否定了他们原本打算证明的猜想。
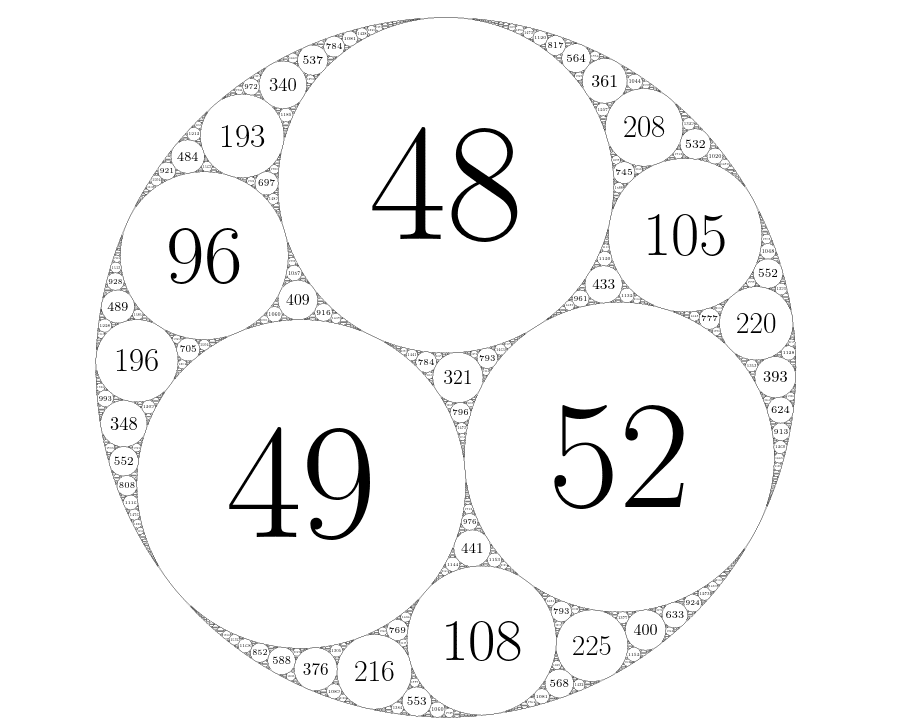
前四个圆的曲率是(-23,48,49,52),生成了约15000个圆。这当前结构里,全局-局部猜想在模24的任意剩余类里均不成立。| 图源:论文THELOCAL-GLOBALCONJECTUREFORAPOLLONIANCIRCLEPACKINGSIS FALSE
凭借经验、审美、乃至哲学主张,很多数学家养成了一种直觉,哪怕不知道如何证明一个猜想,他们也往往能够以较大的胜率,猜测出猜想正确与否。比如说,对于国人熟知的哥德巴赫猜想(任一大于2的偶数都可写成两个质数之和),当代几乎所有的数学家都相信它是正确的,虽然至今没有人知道如何证明它。
几乎所有的数论专家都曾以为,阿波罗尼奥斯垫圆上的局部—全局猜想是真的。不但有很多类似的已知结论支持他们的信念,同时对于这些行家里手来说,他们看不出有什么约束条件,会导致猜想不成立。结果这一次信念崩坍了。
原来,这些圆的曲率在满足笛卡尔定理的时候,会以一种意想不到的方式受制于二次互反律(上一节提到的概念)。
Fuchs说:“没有大量数据模拟,很难想象(他们)能凭运气直接发现这个。”
“这纯粹是巧合。”Haag承认。“如果我没有把数据做得足够庞大,我们就不会注意到它。”
这项工作对数论的未来,是一个好兆头。很多数论学者开始自我反省。例如,在连分数领域里有一个Zaremba猜想,之前大量数学家都相信它也是真的。但在局部—全局猜想被证否之后,人们开始下调自己的信心。“你可以通过直觉、通过证明来获得数学上的经验感悟。”Stange指出,“而且你非常相信它,因为你花了很多时间思考。但你不能和数据争论。”
到此,阿波罗尼奥斯垫圆的故事,可以画上一个临时性的句点。或许,它远不及费马大定理的证明那样恢弘、深邃,但关于这些相切的圆,它们拥有不输任何数学分支的深厚历史,它们具备简单但十分精妙的代数特征,以及目前仅仅揭开冰山一角的极其深刻的算术特性。
在前面提及“如果把每个曲率的数值mod 24,则会出现一条规则”时,不知大家有没有感觉到这个数字24的出现,十分突兀。
其实这个24已经表明我们进入了某片数学深水区。这个数字在理论前沿分支中随处可见,以惊人的方式将不同学科联系在一起。
由于一系列刚刚开始被理解的“巧合”,数字12和24在数学中发挥着核心作用。这一事实的第一个暗示是欧拉的奇异“证明”:
1 + 2 + 3 + 4 + … = -1/12。
上面的欧拉等式现在可以用黎曼zeta函数来赋予严格的数学意义,并且在物理学中它解释了为什么玻色弦理论在26=24+2维中效果最好。
同时,11+22+32+…+242=702,这一事实在弦理论、Leech晶格(是24维空间里最密集的球体堆积方式,又是24!)和Monster群之间建立了一种奇怪的联系。一个更为人所知的、密切相关的事实是“模形式”理论中的12-周期现象。数学家正在尽最大努力揭开深奥的谜团。
阿波罗尼奥斯垫圆本身,实际上对应于作用于某双曲空间上的某个群(“阿波罗群”)的轨道。事实上,阿波罗群是洛伦兹群的一个离散子群,在狭义相对论中非常著名!研究旋量的物理学家对它并不陌生!不过,最困难的还是本文所记述的,关于数论方面的问题。它是非常罕见的,把数学源头——古希腊的几何,与现代最前沿的数学领域之一——自守形式,联系在一起的数学对象。
本文来自微信公众号:返朴 (ID:fanpu2019),作者:嘉伟

