前不久，著名数学家理查德·施瓦茨（Richard Evan Schwartz）宣布证明了有50年历史的哈尔珀-韦弗猜想。用美国宾州大学数学家塔巴奇尼科夫的话说，施瓦茨的学术风格是“喜欢攻克那些表述简单明了但公认很难的问题，而且通常他会看到之前的研究者没有注意到的东西”。
一
莫比乌斯环是分析、拓扑和几何学中一个深刻、重要且基础的概念。然而，令人惊奇的是，和其它现代数学里的研究对象不同，它不但不抽象、难懂，反而还十分地具体和直观：就连小孩子都可以用一条细纸带，轻松制作出莫比乌斯环的模型。
用细长纸带制作莫比乌斯环 | 图源：图书《从麦比乌斯到陈省身：麦比乌斯变换与麦比乌斯带》，刘培杰，哈尔滨工业大学出版社
但是，不知道大家有没有思考过下面的问题：如果我们偏偏不用细纸带，反而选择一条“宽”纸带，比如说一张正方形手工纸（长宽比1:1），那能否在不撕裂纸张的情况下制作出一条莫比乌斯环？（剧透，没有其它附加条件的话，答案是可以。但是需要很巧妙的方法，大家不妨先自行思考一下。）
如果把上面的问题进一步“数学化”，问“宽纸带的长宽之比至少为多少时，我们才能制作出一条光滑的莫比乌斯环？”实际上，在过去整整50年里，数学界对上面的问题始终无能为力——直到今年8月24日，著名数学家理查德·施瓦茨（Richard Evan Schwartz）才以非常巧妙的方式给出了答案（半个多月后的9月13日，他更新了自己的论文）。
二
对于拓扑学中的莫比乌斯环，两位德国数学家——奥古斯特·费迪南德·莫比乌斯（August Ferdinand Möbius）和约翰·本尼迪克特·利斯廷（Johann Benedict Listing）——在1858年同时独立地发现了这一几何结构。（石溪大学的数学家Moira Chas曾考证，高斯在更早的时候便已认知到这种单侧曲面的存在性。）
数学家和天文学家莫比乌斯还被认为是拓扑学的先驱。他最早明确了拓扑学的本性。在1863年出版的《初等关系的理论》（Theorie der Elementaren Verwandschaft）里，他考虑了两个图形，它们的点形成一一对应，并在此对应之下邻近的点对应着邻近的点，他率先建议研究这样联系着的两个图形之间的关系。在随后的160年里，拓扑学——研究几何图形或空间在连续改变形状后还能保持不变性质的学科——蓬勃发展，已然成为数学里最主要的分支之一。莫比乌斯环也显示出非比寻常的重要性。它本身具有很多奇妙的性质，直到今天也未能完全揭示。
如之前提及的、在半个世纪里一直困扰着拓扑学家的“简单”问题：一条矩形纸带，设其宽为单位长度，则其长至少为多少时，我们才能用这条纸带制作出“光滑”的莫比乌斯环？
虽然数学家心目中的纸带，是某种理想的数学对象——单纯是一个可被操作的曲面（不需要考虑其厚度），但仍保留了“物理”纸带的基本特征：①纸不具备弹性，所以不可拉伸；②纸带显然不能在无损的情况下穿过自身。
至于说“光滑”性，通俗地理解，就是要求制作出的莫比乌斯环上没有折痕。从专业角度上讲，光滑曲面是指，曲面上任一点，都存在唯一的切平面。然而折痕上的点，就如同平面上的尖点一样，可以存在多个方向上的切平面。
光滑性的条件是必要的，否则纸带的长度完全可以小于其宽度——相当于改变了问题的性质。回到之前的思考题：一张正方形手工纸，我们能否在不撕裂纸张的情况下，用它制作出一条莫比乌斯环？
答案是，可以。只要把正方形手工纸，如下图折叠出形如手风琴的褶皱结构。把“纸风琴”整体当作是一条纸带，然后按正常莫比乌斯环的做法，把它扭转180度（半圈），再用胶水把插入彼此的两端粘在一起。它形成了一个“压缩”的莫比乌斯环，本质上和常见的莫比乌斯环完全相同，只不过我们无法在不破坏纸结构的情况下把它展成通常的莫比乌斯环罢了。所以，长宽比是1的纸带，在不要求光滑性时完全可以制作出莫比乌斯环。
风琴状的莫比乌斯环 | 图源：Thirty Lectures on Classic Mathematics
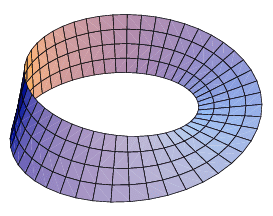
最标准的光滑莫比乌斯环长这样，上面没有“折痕”。但用无弹性的纸带作出的莫比乌斯环和它有外观上的差异。| 图源：笔者利用mathematical生成图像
三
1977年，普林斯顿大学的数学家查尔斯·西德尼·韦弗（Charles Sidney Weaver）和本杰明·里格勒·哈尔珀（Benjamin Riggler Harper Jr）一起，深入探讨了“用纸带制作光滑的莫比乌斯环“的问题。他们发现，纸带长宽比的下确界位于区间
中，但无法确定具体的数值。
他们还指出，“如果允许制作的莫比乌斯自身相交，问题就简单多了。”遗留的问题则可以非正式地表述成，确定需要多少冗余空间来避免纸带自相交。
哈尔珀和韦弗提出长宽比的下确界是，
但他们未能证明这一点，后来这被称为哈尔珀-韦弗猜想（Halpern-Weaver conjecture）。
谢尔盖·塔巴奇尼科夫（Serge Tabachnikov）是宾夕法尼亚州立大学的数学家，他的导师是蜚声全球的拓扑学大师德米特里·福克斯（Dmitry Fuchs）。他们合著了一本教科书Mathematical Omnibus: Thirty Lectures on Classic Mathematics（姑且译为《经典数学30讲》）。在其中的第14讲，他们详细介绍了纸带莫比乌斯环与哈尔珀-韦弗猜想。
2019年，布朗大学的数学系教授理查德·施瓦茨因与塔巴奇尼科夫合作的契机，读到了他们的这本经典教材。“我一读到那一章，就立刻沉迷其中。”他后来说。
四
依据自己在8月24日发布在arXiv.org上的论文，施瓦茨宣布证明了哈尔珀-韦弗猜想。经过其他数学家的快速审校，如今拓扑学界基本上认可了他的证明。
施瓦茨本人是几何群领域里的权威。几何群论是一个相对较新的数学领域，大约始于20世纪80年代末；它探索有限生成群，并寻求其代数性质与这些群作用其上的几何空间之间的联系。他还在台球的路径问题——一种基于平面凸形的动力系统——上作出了重要贡献。
他的研究领域涵盖了动力系统、双曲几何、迭代理论、拓扑学等。2002年在北京召开的国际数学家大会上，施瓦茨受邀做了45分钟的报告；2003年，他又获得了古根海姆奖学金。
Richard Evan Schwartz 于2023年3月22日在牛顿数学研究所讲解Thomson's 5 point problem |图源：Rothschild Lecture: Thomson's 5 point problem - YouTube
不过，最新论文之所以能够被快速接受，除了施瓦茨本人的学术地位和历史信用外，还在于他用到的技术：设法将问题分解成可管理的部分，每个部分本质上只需要基本的（现代）几何技术来解决。德国哥廷根大学的数学家马克斯·沃德茨基（Max Wardetzky）赞叹道：“这种证明方法体现了一种最纯粹的优雅和美丽。”
施瓦茨证明，用于制作光滑莫比乌斯带的纸带，长宽比必须大于。解决这个难题需要很强的数学创造力。“用公式来区分自相交和非自相交的曲面总是很困难的，“《经典数学30讲》的作者福克斯说，“要克服这个困难，你需要有（施瓦茨的）几何洞察力。但这是如此罕见！”
有趣的是，施瓦茨一开始犯下了一个“低级”错误，以至于浪费了几年的时间。如果不是那个错误，“我会在三年前就解决这个问题！”施瓦茨有几分懊丧地说道。
在几何学中，如果一个曲面上的任意一点上均有至少一条直线经过，则称该曲面为直纹曲面（Ruled Surface）。另一种常见的说法是，如果一个曲面可以由一条直线通过连续运动构成，则可称其为直纹曲面。以三维欧几里德空间为例，最常见的直纹曲面是平面、柱面、锥面和马鞍面。著名的莫比乌斯环也是直纹曲面。对于直纹曲面，存在一些方法，可把曲面分解成更简单的平面结构。
完全无弹性的纸带制作出的莫比乌斯环的基本形状。| 图源：澳大利亚的著名科幻小说家Greg Egan
上面这种莫比乌斯环也是直纹曲面。| 图源：澳大利亚的著名科幻小说家Greg Egan
出于某种先入为主的印象，施瓦茨在2021年的论文里错误地认为，由莫比乌斯环分解出来的结构应该是平行四边形。这导致了失败。
在找到成功的证明思路前，施瓦茨尝试了许多其它策略，断断续续地花了近2年时间。他最近决定重新审视这个问题，因为有一种直觉让他感到不安：他在2021年使用的方法应该是有效的。从某种意义上说，他的直觉是正确的。
到今年夏天，施瓦茨决定借助具体的纸带进行实验。在这些实验中，施瓦茨分解了一个莫比乌斯纸带模型，然后意识到，“天哪，分割出来的平面结构根本不是平行四边形。它是一个梯形！”意识到自己的错误，施瓦茨首先感到恼火，然后又决心利用这个新信息来重新计算。“修正后的计算给出了猜想中的数字，”他说，“我惊呆了……我大约三天没有睡觉，就为了把证明写出来。”
五
终于，这个有50年历史的猜想得到了证明。“尝试解决一个长期悬而未决的问题需要很大的勇气。”塔巴奇尼科夫说，“这是理查德·施瓦茨的学术风格：他喜欢攻克那些表述简单明了但公认很难的问题。而且通常他会看到之前的研究者没有注意到的东西。”
至于相关的问题，数学家们已经知道可嵌入自身的莫比乌斯带没有长度限制（尽管在物理上制作它们会很麻烦）。然而，没有人知道如果要用纸条制作一个扭转了3次而非1次的莫比乌斯带，纸条可以有多短。“关于奇数次扭转的莫比乌斯带的最优长宽比的问题，”塔巴奇尼科夫说，“我期待着有人在不久的将来解决这个更一般的问题。”
从另外的角度来说，施瓦茨的证明也不是这个问题的终点。他的证明只适用于光滑的莫比乌斯带，而不是有角或折痕的莫比乌斯带。这些非光滑的莫比乌斯带应该会有更小的尺寸（参考前面的思考题），因为它们可以在边缘处折叠在一起。
在光滑的条件下，长宽比的下确界是取不到的。要想达到下确界，只能得到这种退化的三角形莫比乌斯环。| 图源：The Optimal Paper Moebius Band，2308.12641.pdf (arxiv.org)
从更宽泛的角度说，对纸带莫比乌斯环的研究，属于一个非常年轻的数学分支——Paper Sheet Geometry（或可译作“折纸几何学”）。
Paper Sheet Geometry是研究纸张的形状、性质和变换的数学。它涉及到如何用纸张制作各种几何图形，如多边形、曲面和立体，以及如何用纸张解决一些几何问题，如折叠、剪切和划线。它的一个重要应用是折纸艺术，也叫做Origami。Origami是一种将一张平面的纸张折叠成各种复杂的三维形状的技术，如动物、花卉和星形。Origami有很多规则和公理，可以用来描述纸张的可折叠性和可构造性。
Paper Sheet Geometry的另一个应用是纸板工程Cartonage（纸板包装，法语词）。Cartonage是一种将多张纸板或硬纸板剪切、折叠和粘合成各种实用的物品的技术，如盒子、文件夹和书籍。
Cartonage还需要考虑纸板的厚度、强度和稳定性。Paper Sheet Geometry则与其他数学领域相结合，如拓扑、代数和组合学，制造了不少令当代数学家一筹莫展的难题。
这样的数学领域不仅能够直观揭示抽象对象的复杂性，还能够将数学与我们日常生活联系起来，形成一个个引人入胜的课题。而莫比乌斯环也并不仅仅局限于数学领域。它在日常生活中也有一些有趣的应用。
工业领域也利用了莫比乌斯环的原理。莫比乌斯传输带是一种特殊设计的传送带，使平带由原来的内外两个表面变成循环的“单面”。被运输物料对输送带所引起的应力由单面承受变为双面循环，从而可以延长输送带的使用寿命。
同时，由于其非常“平易近人”的特性，莫比乌斯环在艺术作品中广泛出现。实际上，它是仅次于黑洞的科学“明星”概念。艺术家们常常使用这个形状来探索空间和形态的独特性质。莫比乌斯环的无限性质以及与时间和空间的交织，使其成为许多艺术作品的灵感来源和构成要素。
如1988年在日本上映的动画电影《机动战士高达：夏亚的逆袭》中，以莫比乌斯带作为对命运的隐喻：人类就好比行走在莫比乌斯带上的蚂蚁一般，永远逃不出这个怪圈，不断重复着相同的错误，类同的悲剧也在不断地上演。
最后再分享一则相关轶事。主人公是少年时期的美国物理学家理查德·费曼和他当时的女友阿琳（Arline Greenbaum，后成为费曼的妻子）。阿琳提到她们的哲学老师有一句口头禅：任何事物都像纸一样拥有两面性。费曼则说这一观点本身需要重新思量，然后拿出一张纸，在女友面前凭借从百科全书里学到的知识，现场制作了一个莫比乌斯纸环。阿琳非常惊喜，第二天便把纸环带到了学校。当老师拿起一张纸又开始举例事物都有两面性时，她兴奋地举起了莫比乌斯纸环，令在场的师生们都为之惊讶。
后记
十年前，笔者凑巧也读到过《经典数学30讲》，也曾经被书中第14讲的莫比乌斯纸环问题所吸引，因此对哈尔珀-韦弗猜想的难度有相当程度的直观认知。
所以，在十年后的今天竟然能亲眼见证猜想被证明——还是被阅读了同一教材，被同一问题所吸引的拓扑学权威以相对基础的技术给出的证明——完全出乎了我的意料，令我颇为激动。这也是促使我写作本文的动因。
本文来自微信公众号：返朴 （ID：fanpu2019），作者：嘉伟