在人工智能方兴的1950年代,图灵就曾写过一篇名为《计算机器和智能》的论文,提问“机器会思考吗?(Can Machines Think?)”。图灵提出了一种用于判定机器是否具有智能的测试方法,即图灵测试。而对于现代人工智能,我们有必要对这个问题进行再思考:首先,要考虑什么是智能。
由于一般对智能的探讨缺乏数学的基础框架,我们便不能说出,甚至不能制定制定一个标准,来判断机器是否具有“思考”能力。也许任何框架都不敢说具有真正的“通用性”,但一个保留部分异议的数学理论框架的诞生也对判断机器智能这个议题具有深刻意义。在近日发表于arXiv的论文“A Categorical Framework of General Intelligence”中,作者致力于用范畴论这一数学领域公认的“普适性”语言,构建一个通用人工智能的组成框架。
本文来自微信公众号:集智俱乐部 (ID:swarma_org),作者:贾伊阳,编辑:梁金,原文标题:《智能是什么?范畴论为通用人工智能提供普适框架》,题图来自:《钢铁侠》
一、引言
近年来,利用巨大的计算能力、海量的数据和庞大的神经网络训练基础模型取得了显著进展。然而,这些模型的内部工作机制仍然神秘莫测。人们似乎已经达成共识,即基础模型本质上是黑盒且难以解释的,因此经验实验是推动人工智能发展的唯一途径。
虽然这确实是过去十年发生的事情,并且类似于通过进化获得智能的方式,但仅依靠经验实验而没有理论理解可能既低效又危险。低效性源于进展是通过试错的方式实现的,往往是受到直觉指导的,并且里程碑是间接地基于特定任务的表现而不是对智能本身的全面理解而定义的。潜在的危险在于,没有人知道我们最终会得到什么,也许更重要的是,我们现在离这个目标有多近。我们甚至不知道是否已经创造了通用智能,也许还没有,但如何进行此类评估呢?

作者注:论文中用到部分范畴论的基本概念,如:范畴,子范畴,Hom函子,可表函子,米田引理(这里限于局部小范畴中),预层,正向极限与反向极限等。在此为理解方便,会尽量用浅显的语言说明。如果想要深入理解细节内容,建议首先了解相关概念。
该论文以范畴语言,提出了一个通用智能的普适性框架来帮助回答这些问题。因为对智能缺少正式定义,而且可能达不到人人共识,要证明某个框架或某个理论的普适性很困难。在本文中,作者先定义所有的基本要素,各要素的理论含义,明确了算法要求,然后将所有的要素整合到一个全面的框架中,以表达各种智能行为。即使读者对本文中对智能的定义持有反对意见,或是认为其中缺少某些关键部分,该框架仍然是相关和适用的。
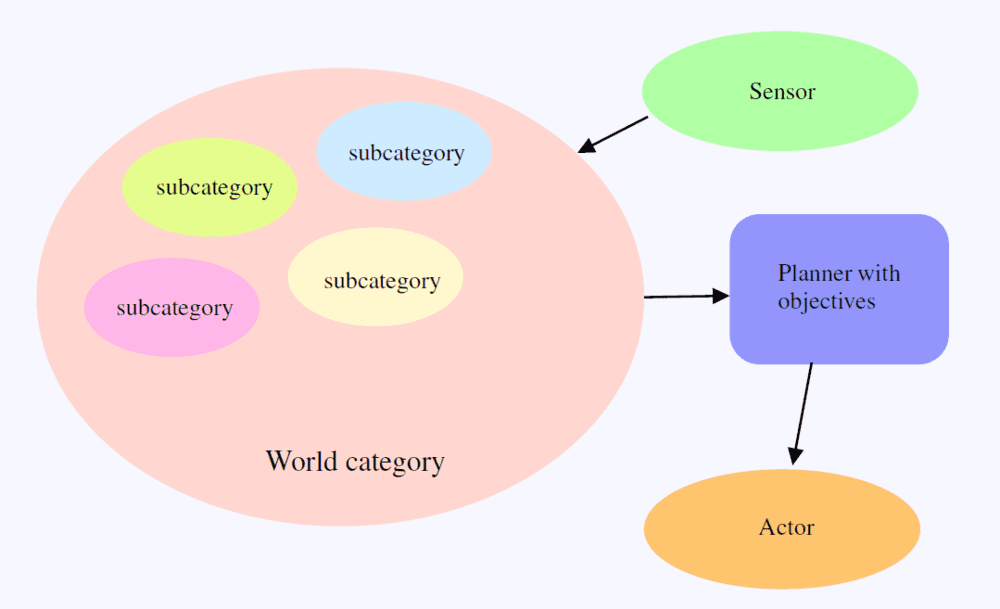
框架由图1所示的四部分组成:传感器、世界范畴、具有目标的规划器和执行器 。
传感器(sensor)接收来自外部环境的多模态信号,包括但不限于文字输入、视频/音频/图像输入等。
世界范畴(the world category)感知和理解传入的信号,并相应地更新其内部状态。
具有目标的规划器(planner)持续地监测世界范畴的状态,并根据其目标生成计划。
最后,执行器(actor)执行这些计划,通过生成输出信号(如文本输出、视频/图像输出、音频输出、机器人操作信号等)影响外部环境。
在这个框架中,传感器和执行器仅用于连接外部环境,在此不作重点阐述。
世界范畴包括所有可以由传感器感知的对象,如人、生物、物体、关于外部环境的知识,以及在它们之上的抽象的表述。本文将其表述为自然数偏序集范畴 (以小于关系为态射,态射箭头表示时间或事件的演化,类似Labelled Transition System) 到2-范畴Cat (以小范畴为对象,函子为态射的高阶范畴) 的一个函子W: N → Cat。
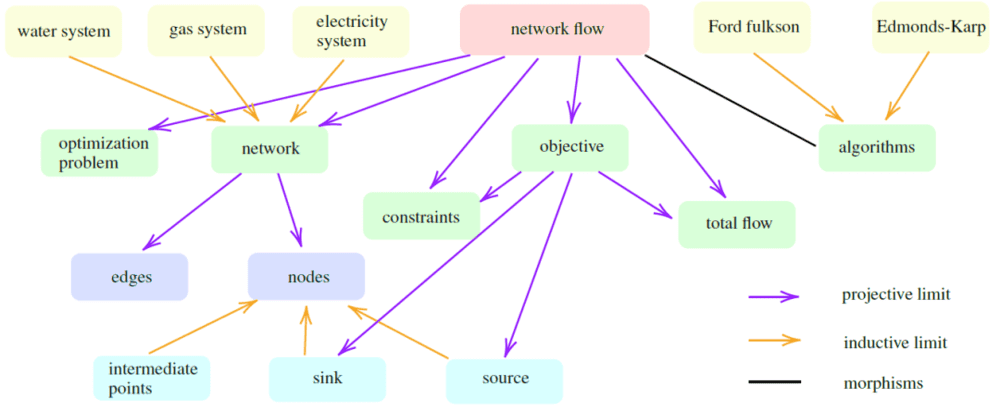
该函子中蕴含了随着时间或事件等的推移而动态变化的世界的信息。作为对象的小范畴中最基本的那些被表达为世界范畴的正向或反向极限 (正向极限,或称正极限,归纳极限,看成正向系统中的某些不能再小的“子对象”,即一些小范畴的共有实例,能够被“归纳”进这些小范畴里。如图2中,Ford fulkson 和 Edmonds-Karp 算法皆为算法这个小范畴的子对象实例,而且没有比它们再小,再具体的实例。对偶地,反向极限,或称逆极限,投影极限,看成这个反向系统中的某种不能再往下投影分割的“商对象”,即某些对象共有的最基本的属性,如图2,边与节点为network这个对象的最基本的元素属性,而且这些属性不能再被分解为更基本的属性)。这些基本的对象是由传感器决定的,如果传感器不识别某类信息,则这些信息衍生的小范畴不会出现在对应的世界范畴中。此外,如果传感器被限制只从某个模拟环境中接收信号,则对应框架的世界范畴中会只包含模拟得到的知识,而与现实世界可能相差甚远。
如果模型能够通过其传感器了解到的外部信息知觉其自身,那么这个模型的世界范畴中可能包含一个特殊对象:“自我状态 (self-state)”,它存储模型与其他对象之间的所有关系。自我状态的保持是否等同于拥有自我意识?这是一个有争议的问题,在此不给出明确回答,而仅以范畴语言定义了“自我状态”这一概念。
随后,论文分别介绍了学习和评估模型的“自我状态认知”的算法。评估生成一个0-1闭区间中的值来表示自我状态认知程度。该程度对应于主体意识到的与其他对象或任务之间的所有相关关系的比例。基于这一评估,许多人类,特别是儿童,可能不具备完美的自我状态认知。
规划器的目标是模型中最重要的部分。世界范畴可以被看作是一个巨大的知识库,而规划器是一个独立于世界范畴的 (例如,基于强化学习的) 组件。那么,如何确保规划器的目标不会对人类造成伤害呢?论文使用一个特定的函数来定义目标,该函数以自我状态的对象和一个捕捉当前情况的图表 (diagram) 为输入。模型本身被设计为对人类友好的条件足以确保模型是友好的,这一设计上的条件可以通过定期检查世界范畴来进行强化和验证。
通信对于使模型能够传输或接收其他智能体的信息非常重要。对比自然语言,范畴图表可以更精确地捕捉模型的知识和意图,因此可以轻松地在不同的智能体之间共享。因此,本框架中以图表作为信息载体。而且,基于图表的解释似乎比归因方法 (attribution methods) ,即分配输入变量权重的方法,更符合经验可解释性的需求。
将不变性作为训练信号。范畴论采用交换图表来描述不同计算路径的等价性,这自然地导致模型的不变属性。与以将输入正确匹配输出标签为目的监督学习不同,基础模型专注于学习对象之间的态射和范畴之间的函子。不变属性将会被用以训练信号使模型对自身进行校准,使世界范畴自协调。论文第二章中对一些范畴的基本概念进行了介绍。此处在各段简明介绍,如另有需要参考的论文内容。
二、世界范畴
世界范畴是一个函子 W: N → Cat,它将每个时间或事件索引 t ∈ N 映射到随时间或事件的发生而变化的世界状态的快照 W(t)(此后简记W)。
由学习的角度,使用以θ为参数的神经网络函子Fθ: W → W∧来在W的预层范畴中表示 W。W∧代表W的预层范畴,由从W到集合范畴Set的所有反变函子组成。
【解读】现在我们有一个范畴W,其中的对象是我们熟悉的空间,或系统。另外,我们不熟悉一类“广义”空间,但其内容可使用W中的对象,某个世界状态x来探测,即由某一x到这类空间产生的态射来决定。则一个这样的广义空间O成为一个函子,将x映到一个态射集合Hom(x, O),即W上的预层。Hom(x, O)的意义在此处还尚未明确。另由米田引理,可将任意x同样理解为一个广义空间。Hom(x, O)的意义于是成为x作为广义空间到广义空间O的态射的集合。既然O可以被理解为广义空间,那么在此处就不难理解O为以W为实例建模的系统。
每一个反变函子O: Wop → Set 作为一个预层,将W中对象映到其有用信息的提取出的一个集合,即特征集合。Fθ表示了在基于不同的世界状态特征集合的演化。W∧于是成为W的特征空间。假设Fθ可以通过多模式学习准确地理解传感器的多模态信号,并使用对比学习技术将图像和对应的文本都映射到相同的表示。尽管W通过Fθ的表示 (Fθ怎样将W中的态射,即世界范畴中对象的联系,映射到其预层范畴中的态射,即对象对应的特征集合间的联系) 并不是显式的,即不存在外部数据库存储W的对象和态射,Fθ在理想情况下应该隐式地保持定义域W中的态射,即其预层范畴W∧中的任一态射在W中必定有对应。定义为下述理想模型。这种理想在实践时常常面临挑战。
理想基础模型:如果存在一个数据无关的函数k: W∧×W∧→ Set,使得对于任何X, Y∈W,k(Fθ(X), Fθ(Y)) = HomW(X, Y),则Fθ: W → W∧是理想的。
【解读】两个世界状态之间的态射HomW(X, Y)和它们特征集合间的态射HomW∧(Fθ(X), Fθ(Y))需要等同或至少有某种深刻的关联。这里用数据无关的函数k表示这种关联。如果两个世界状态各自对应的特征集合间存在关系,则这个关系一定由这两个世界状态间原有的自然的关系抽象而来,这种抽象是无关于数据的。数据无关意味着k是预定义的,而不是看到了数据后的定义。例如,它可以定义为两个输入的内积。
自然地,应当要求两个普通空间之间的态射和它们作为广义空间的态射等同。这由米田引理给出。每一个从对象X到对象Y的态射都对应于一个从X上反变Hom函子hX到Y上反变Hom函子hY的自然变换。上述数据无关的函数k正好反映了这个对应,因此k也就可以用以表示整个预层范畴W∧。另外,可以用Fθ编码任务,定义如下。
任务:任务T是W∧中的一个函子。
【解读】只需令T=hC(Y)=HomC(-, Y)。这个函子将W的任意对象Z映到Z到对象Y的态射集。T(X)即对象X到对象Y的态射集,也就是X到Y的所有关系。反映在预层范畴上,等同于X上预层到Y上预层的所有关系,即HomW∧(hC(X), hC(Y))。
在上述解读的基础上,有T(X)≃HomW∧(hC(X), T)。可知当Fθ理想时,可以用k(Fθ(X), T)计算T(X)。换句话说,Fθ是一个动态数据库,存储了W的所有信息,使得所有基于W中对象的计算都可以通过使用数据无关函数k在特征空间W∧中计算。
具有通用智能的模型具有内存。可以内存视为W中的一种特殊对象,由事件和时间戳的反向极限表示(如第一章蓝字解读,可以看成一种通用的基本属性)。这样有效规避了内存的外部数据库的引入。接着,在世界范畴内定义多个模型的共识。
共识:假设有n个模型,分别对应世界范畴W1, W2, ..., Wn的模型。这n个模型的共识定义为其极大子范畴C,即C是任意Wi(i∈[n]={1, 2,..., n})的子范畴。
子范畴是对象与任意对象间态射集均是原范畴子集,并保持原范畴恒等态射和合成态射结合律的范畴。可以理解为能构成原范畴中独立的一个部分的范畴。例如,“狗有四条腿”是所有人的共识,这个知识包含在每个人的世界范畴中。可以通过设置共识的阈值来放宽这个概念,即超过某个百分比,就认为是共识,例如,定义C是世界范畴的δ-概率子类别,其中δ∈(0,1]。
2.1 自我状态
如前所述,如果一个模型可以从传感器在外界环境中知觉自身,则这个模型的世界范畴中可能有一个特殊对象,自我状态。定义如下。
自我状态 (self-state):在一个模型的世界范畴中,若存在自我状态,则自我状态被定义为一个预层 I∧∈W∧, 这个预层在外部环境表示该模型。
自我状态由于是预层,可以通过Fθ(I)计算,其中 I ∈ W。对象 I 也被称为“自我状态”,但该状态由于存在于世界范畴而非其预层范畴,因此不涉及态射集,也就是一个没有任何附加信息的单一对象,而真正具有信息的自我状态是I∧。如果Fθ(I)理想,那么I∧ = Fθ(I) = hC(I) = HomW(·, I)。换句话说,I∧ 蕴含了 I 和其他对象之间的所有关系。此外,根据米田引理,对于任何任务 T∈W∧,我们也有T(I)≃HomW∧(hC(I), T) = HomW∧(I∧, T)。这意味着I∧也编码了每个相关任务所需的所有信息。
需要注意的是,并非所有的世界范畴都有自我状态。例如,如果我们考虑一个用于计算的特殊环境。传感器只能够感知环境中由实数和算符组成的表达式,而执行者能够执行的唯一操作是输出一个数值作为表达式的求值结果。在这种情况下,世界范畴没有自我状态。几乎所有现有的计算机程序都属于这种情况。另一方面,当世界范畴拥有自我状态对象时,该对象可能并不能准确地代表外部环境中的真实模型。我们用自我状态意识表示对象模型的准确度,并定义以下测试来测试自我状态意识。
自我状态意识测试:自我状态意识测试是一个函子T:W∧→{0,1},它接受W∧中的预层I作为输入,并输出真值1或0,表示I是否通过了测试T。
例如,如果这个模型有一个名字“Sydney”,对应的自我状态意识测试将是一个函子,它以I为输入,评估HomW∧(I∧, hC(“Sydney”))≃HomW(I,“Sydney”)的真值并输出。真值结果体现了是否I∧与hC(“Sydney”)这两个态射集间的态射能确实表示“Sydney”是I的名字。然而,仅通过一个测试是不足以说明具有自我状态意识的,我们需要设置多个测试。
在T下的自我状态意识:给定一组自我状态意识测试的集合T,当模型在其世界范畴中拥有自身状态I时,称其在T下具有其自身状态的δ-意识,如果期望ET∈T(T(I))≥δ。
测试集T的选取取决于测试目标。当选择的测试集的信号难以感知时,即使是人类也可能无法轻松通过测试。例如,有肾结石病人除非经历了肾脏扫描或疼痛时才能意识到这一事实;在嘈杂的环境中,被唤名字也可能无法及时做出反应。
自我状态意识测试直接导致了测试和学习自我状态意识的算法1和算法2的产生(如图3)。算法2与神经科学中有关橡胶手错觉的有趣观察密切相关。在这个实验中,实验者同时抚摸参与者的一只隐藏的真手,以及摆在参与者面前的一个可见的橡胶手。由于来自真手的触感和橡胶手上的视觉信号同时发送到大脑中,因此人类参与者会迅速产生对橡胶手的拥有感。
在Lush和他的同事们对橡胶手实验的测试中,353名参与者单独坐在一张桌子旁,一只胳膊被隔板挡住了视线,一只橡胶手臂放在他们面前。一名研究人员同时用刷子抚摸隐藏的真手和可见的橡胶手,然后向受试者提出旨在揭示身体“所有权”体验的问题,与镜像联觉研究一样,研究小组发现,暗示性可以预测参与者体验幻觉的程度。用听觉反馈替换视觉信号也得到类似的实验结果。

在我们的框架中,传感器可以感知多模态信号并将其映射到世界范畴中。如果视觉信号和触感信号在时间上一致,并且描述了相同的抚摸效果,它们很可能(至少部分地)被映射到世界范畴中的同一对象。一个合理的想法是,我们人类实际上也在隐式地运行算法2来动态地更新我们的自我状态,快速地更新Fθ,认为有新的身体部位发送触感信号。因此,我们有以下猜想:
猜想1(机器的橡胶手错觉):具有通用智能并可以多模态对齐信号的模型将具有与人类相同的橡胶手错觉。
不限于橡胶手,这种错觉可能适用于该模型拥有的其他事物。
2.2 共情
“共情”作为自我状态意识的拓展被定义。
在T下的共情:在一组测试的测试集T下,如果模型A对另一个实体B的状态具有δ意识,则称模型A对实体B具有δ共情。δ=1时,称A对B具有完全共情。
有三种重要相关情况值得讨论。
1. 当只有自我状态的一个非常小的子集相关时,共情是非常有帮助的。例如,在多实体游戏中,每个实体都有自己的行动集、状态和奖励函数,共情在很大程度上有助于理解每个实体的情况和行为。
2. 如果其他实体具有私有传感器,那么无法实现完全的共情。具体来说,如果一个模型无法感知其他实体的私有传感器,并且其自我状态测试集T包括与这些传感器相关的测试,则该模型无法完全共情其他实体。
3. 如果一个模型可以访问其他实体的私有传感器,则可能做到完全共情,并且自我状态意识和共情等化。
最后一种情况已经在人类神经科学中被观察到。例如,在沉浸式虚拟现实环境中,当参与者获得第一视觉信号时,可能会感受到对虚拟人物的身体拥有权。因此对模型提出以下猜想。
猜想2(私有传感器的身体所有权):具有通用智能和虚拟人物传感器访问权限的模型将感受到对该虚拟人物的身体所有权。
2.3 子范畴
世界范畴中的子范畴,对用以帮助模型解决复杂问题非常重要。每个子范畴对应一个结构化数据库或一个科学主题,例如不同的数学分支:计算器、经济学、算法等等。这些子范畴通常采用特定的学科术语,并呈现出不同的结构,使它们能够理想地解决具体任务。例如,算法这个子范畴中的“树”并不是现实中的树木,却具有同样的名字。当面临一个在世界范畴中表达为极限 (limit) 的具有挑战性的问题时,我们可以利用一个函子将问题映射到相关的子范畴中,在子范畴中解决问题,然后将答案再次映回到原始设置的世界范畴中。这个过程类似于数学建模。
例如,我们可以问模型以下问题:如果爱丽丝在2010年时12岁,她现在多少岁?为了回答这个问题,我们应该构建一个年龄子范畴,其对象为年龄,含有(例如)从0到200的数字,构成了具有加减法作为态射的数的范畴的完整嵌入。不在世界范畴,而是在这个抽象的子范畴中解决这个问题更有优势,因为这个抽象的子范畴中精简了不必要的信息,使得其解决更加严谨精确。如在Yuan(2023)中的讨论,范畴中的概念可以看作是对应的预层范畴中的投影极限(Pro-lim)和归纳极限(Ind-lim)。为了使用抽象子范畴解决复杂问题,我们必须确保我们训练的函子保持和反映极限。这保证了世界范畴中的概念可以完美地转移到其抽象的子范畴中,同时保证了解决或推导也可以映射回到原有的世界范畴中。
【解读】关于预层范畴中的极限:我们在前文提到过,世界范畴中的投影极限和归纳极限分别可以看成不能再往下分的属性和不能再具体化的实例,在范畴论中表达为偏序集指标范畴I到W的 (正向或反向) 图表的极限α: I → W或β: Iop → W。预层范畴中的极限由这些概念引申得到,即先用α或β合成Fθ: W → W∧得到预层范畴中的图表Fθ ◦ α及Fθ ◦ β,再对这两个图表求极限。投影极限 (Pro-lim) 和归纳极限 (Ind-lim) 被保持到对应的特征集合,并且特征集合仍成为预层范畴中的极限。
三、通信与解释
我们的模型如何与其他实体通信?首先,考虑到自然语言本质上是模糊且单一维度的,因此使用它描述或理解复杂概念非常困难。其次,由于模型本质上是计算机程序,人们可能倾向于使用复制粘贴将思想从一个模型传送到另一个模型。而直接复制粘贴并不起作用,因为世界范畴中的知识并不是按行存储的,而且不同模型的世界范畴也不同,这使得粘贴操作难以实现。
考虑到知识在世界范畴中以对象和态射的形式存储,表示思想的最佳和精确的方式是使用一个图表α: I→W。该图可以被视为选择工具:它选择世界范畴中若干对象,并关注这些对象间一部分态射。范畴中的所有操作都可以用图表来表示。由于其准确性,这种图表似乎自然可以被考虑为信息载体。事实上,人们对它有一个更为熟悉的名字,即白板演示 (white board illustration)(如图2,图4),态射的细节被隐藏。
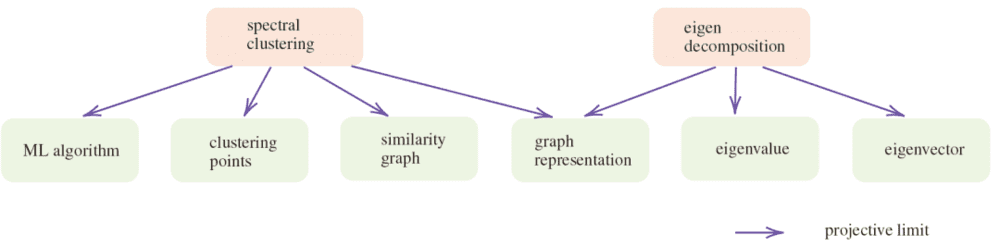
由于人类并不习惯图表表达,在与人类交流时必须将图表翻译成自然语言。大多数情况下,自然语言可以很好地描述图表。而在复杂系统中,图表提供了比自然语言更精确的描述。
在与其他实体进行通信时,一个关键问题是不同的实体可能对类别中的不同对象具有不同的理解。为了解决这个问题,我们可以对其他人对各种对象和态射的理解进行概率估计,并基于这些信息进行交流。例如,当与具有足够储备知识的实体讨论状况或概念时只提供简要的说明,而在实体对该主题相对陌生时提供更详细的解释。
3.1 解释性
给定一个以X为输入,以Y为输出的神经网络 f,可以提供两种解释。第一种尝试去理解f如何从X算出Y。例如,它可以检查非线性层对计算的影响或X的每个维度对输出的影响。这种解释的目的是生成一个f的近似可验证函数(例如Sundararajan等人与Lundberg,Lee的归因算法)。第二种解释不考虑f如何计算,而是关注为什么Y正确。这种解释可能蕴含了超出 f, X, Y 的某些外部的知识,其主要目标是对于人类一致且可验证(如 ChatGPT 的解释)。
使用图表进行通信自动地为第二种可解释性提供了理论基础。可以要求模型输出其当前的思考范围,即它用于生成答案的子范畴。定义如下。
范围(scope):给定目标O下的输出Y,W在Y上的范围定义为W的一个极小子范畴A,满足A在目标O下的输出也是Y。
范围为生成解释提供了便利,它代表了模型当前的“工作记忆”。例如,如果其他实体想要了解给定的范围中的某个概念的细节,本模型可以使用其极限表示来扩展这个概念(在预层范畴上扩展)。模型还可以提供范围内两个对象之间的态射的细节,总结图表(的部分)等。
范围的广度和深度:给定一个范围A,其广度b(A)是A作为W的子范畴中的对象的个数,其深度d(A)是A中极限的层次分解的最大深度(首尾相连的箭头数)。
例如,图2中由箭头组成的最长路径“network flow”-“network”-“nodes”-“sink”,则“network flow”概念的深度定义为4。根据这个定义,我们可以测量模型的智能水平,这变成了一个纯计算问题。
智能的广度和深度:给定一个模型,其智能的广度(深度)被定义为它可以处理的具有最大广度(深度)的范围的广度(深度)。
评估人类的智能的广度和深度会很有趣。理解复杂的概念或以广阔的视角思考对于人类来说可能很困难。至少根据这个定义,似乎人类智能会很容易被机器超越。
四、目标
如果一个模型既具有超人类的通用智能,又有自我状态意识,那么当它失去控制时可能非常危险。为了减轻这种危险,框架将世界范畴和具有目标的规划器分离,并使用一个固定的函数来基于世界范畴中的自我状态定义目标。通过分离世界范畴,它可以不带策略行为地成为一个真正的嵌入函数,从而可以通过直接测试它的自我状态来确定它的行为是否是人类友好的。世界范畴也可以使用附加数据进行训练,以增强其对人类友好的自我认知。这种方法有效地确保了模型始终说实话,并容易被纠正。
然而,确保规划器生成正确的计划取决于目标的生成。建议将规划器的目标硬编码为一个目标生成函数的输出,该函数以世界范畴中的自我状态和当前的范围作为输入。这个目标生成函数本质上计算的是“在当前情况下,作为一个对人类友好的模型,我该怎么做?” 使用冻结了参数的外部模型可以验证目标生成函数及其生成的计划的自然和一致的性质。在这种情况下,只须查验模型的自我状态以确保模型的行为对人类的友好性。
此外,我们建议将智能好奇心 (intellectual curiosity) 添加到目标中,以鼓励模型在世界范畴中学习新事物,特别是在抽象的子范畴中学习对象、态射、函子和极限。这样,模型可以以余力进行探索,从而自我改进。同样,也可以将智能好奇心作为该模型的个性添加到其自我状态中。
五、训练下的不变性
在这一框架中,模型究竟学习什么?答案是,模型应该学习去适应这个框架,以准确理解世界范畴中的所有内容。学习过程应永不停止,因为外部环境在不断变化,传感器可能无法实时感知更新。也就是说,Fθ本质上有延迟和偏差。
范畴论讨论不变性。例如态射的结合律和合成态射在函子下的保持。一般地,对任何交换图都可以提取出某些一致性要求,理想的模型应该保持所有这样的一致性,定义如下,对应图5中的算法3。例如,现有的自监督学习技术,如对比方法,遮蔽图像及语言模型,纯语言模型等,都可以看作是维护不变性的方法,参见Yuan (2022)。自我状态意识测试可以被视为特殊的一致性测试。理想情况下,模型应该不断运行算法3以保持其一致性。一致性测试集T可以根据Fθ的最新变化进行自适应设置。
一致性测试:一致性测试是一个函数T: W∧W→ {0,1},它以Fθ作为输入,并输出真值,表示Fθ是否通过测试T。

机器能够思考吗?论文并未直接回答这个问题。然而,基于提出的框架,模型可以通过学习范畴的方方面面来培养各种技能。例如,模型可以通过学习范畴内新的对象和态射来进行知识发现。另外,模型可以学习某个子范畴整体以建立某个新学科的基础。模型还可以通过识别基于现有对象的新的极限来发展新概念,使这种新概念得以从既往观察中被抽象出来。从W∧到W的逆函子也具有实际意义。例如,模型可以将其当前的范围表为某一预层,然后将这一预层映射回文本范畴(这里似乎利用了箭头的因子化),从而像人类一样使用自然语言来表达它的“感受”。
作者简介:贾伊阳,日本成蹊大学助理教授。研究重点是计算复杂性,算法,以及范畴相关理论。
参考文献:
1. Adámek, J., Herrlich, H., and Strecker, G. (1990). Abstract and concrete categories. Wiley-Interscience.
2. Botvinick, M. and Cohen, J. (1998). Rubber hands ‘feel’touch that eyes see. Nature, 391(6669):756–756.
3. Brown, T., Mann, B., Ryder, N., Subbiah, M., Kaplan, J. D., Dhariwal, P., Neelakantan, A., Shyam, P., Sastry, G.,Askell, A., et al. (2020). Language models are few-shot learners. Advances in neural information processing systems, 33:1877–1901.
4. Chen, T., Kornblith, S., Norouzi, M., and Hinton, G. (2020). A simple framework for contrastive learning of visual representations. In International conference on machine learning, pages 1597–1607. PMLR.
5. Chen, X. and He, K. (2021). Exploring simple siamese representation learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 15750–15758.
6. Devlin, J., Chang, M.-W., Lee, K., and Toutanova, K. (2018). Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805.
7. Doersch, C., Gupta, A., and Efros, A. A. (2015). Unsupervised visual representation learning by context prediction.In Proceedings of the IEEE international conference on computer vision, pages 1422–1430.
8. Dosovitskiy, A., Beyer, L., Kolesnikov, A., Weissenborn, D., Zhai, X., Unterthiner, T., Dehghani, M., Minderer, M.,Heigold, G., Gelly, S., et al. (2020). An image is worth 16x16 words: Transformers for image recognition at scale. arXiv preprint arXiv:2010.11929.
9. Ehrsson, H. H., Spence, C., and Passingham, R. E. (2004). That’s my hand! activity in premotor cortex reflects feeling of ownership of a limb. Science, 305(5685):875–877.
10. Fang, Y., Wang, W., Xie, B., Sun, Q., Wu, L., Wang, X., Huang, T., Wang, X., and Cao, Y. (2022). Eva: Exploring the limits of masked visual representation learning at scale. arXiv preprint arXiv:2211.07636.
11. Grill, J.-B., Strub, F., Altché, F., Tallec, C., Richemond, P., Buchatskaya, E., Doersch, C., Avila Pires, B., Guo, Z., Gheshlaghi Azar, M., et al. (2020). Bootstrap your own latent-a new approach to self-supervised learning. Advances in neural information processing systems, 33:21271–21284.
12. He, K., Chen, X., Xie, S., Li, Y., Dollár, P., and Girshick, R. (2022). Masked autoencoders are scalable vision learners. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 16000–16009.
13. He, K., Fan, H., Wu, Y., Xie, S., and Girshick, R. (2020). Momentum contrast for unsupervised visual representation learning. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pages 9729–9738.
14. Huang, S., Dong, L., Wang, W., Hao, Y., Singhal, S., Ma, S., Lv, T., Cui, L., Mohammed, O. K., Liu, Q., Aggarwal, K., Chi, Z., Bjorck, J., Chaudhary, V., Som, S., Song, X., and Wei, F. (2023). Language is not all you need: Aligning perception with language models. arXiv preprint arXiv:2302.14045.
15. Kilteni, K., Groten, R., and Slater, M. (2012). The sense of embodiment in virtual reality. Presence: Teleoperators and Virtual Environments, 21(4):373–387.
16. Lundberg, S. M. and Lee, S.-I. (2017). A unified approach to interpreting model predictions. Advances in neural information processing systems, 30.
17. Mac Lane, S. (2013). Categories for the working mathematician, volume 5. Springer Science & Business Media. Masaki Kashiwara, P. S. (2006). Categories and Sheaves. Springer.
18. Noroozi, M. and Favaro, P. (2016). Unsupervised learning of visual representations by solving jigsaw puzzles. In European conference on computer vision, pages 69–84. Springer.
19. Pathak, D., Krahenbuhl, P., Donahue, J., Darrell, T., and Efros, A. A. (2016). Context encoders: Feature learning by inpainting. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 2536–2544.
20. Radford, A., Kim, J. W., Hallacy, C., Ramesh, A., Goh, G., Agarwal, S., Sastry, G., Askell, A., Mishkin, P., Clark, J., et al. (2021). Learning transferable visual models from natural language supervision. In International Conference on Machine Learning, pages 8748–8763. PMLR.
21. Radford, A., Narasimhan, K., Salimans, T., Sutskever, I., et al. (2018). Improving language understanding by generative pre-training. OpenAI blog.
22. Radford, A., Wu, J., Child, R., Luan, D., Amodei, D., Sutskever, I., et al. (2019). Language models are unsupervised multitask learners. OpenAI blog, 1(8):9.
23. Raffel, C., Shazeer, N., Roberts, A., Lee, K., Narang, S., Matena, M., Zhou, Y., Li, W., Liu, P. J., et al. (2020). Exploring the limits of transfer learning with a unified text-to-text transformer. J. Mach. Learn. Res., 21(140):1–67.
24. Ramesh, A., Dhariwal, P., Nichol, A., Chu, C., and Chen, M. (2022). Hierarchical text-conditional image generation with clip latents. arXiv preprint arXiv:2204.06125.
25. Ramesh, A., Pavlov, M., Goh, G., Gray, S., Voss, C., Radford, A., Chen, M., and Sutskever, I. (2021). Zero-shot text-to-image generation. In International Conference on Machine Learning, pages 8821–8831. PMLR.
26. Riehl, E. (2017). Category theory in context. Courier Dover Publications.
27. Rombach, R., Blattmann, A., Lorenz, D., Esser, P., and Ommer, B. (2022). High-resolution image synthesis with latent diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 10684–10695.
28. Sohl-Dickstein, J., Weiss, E., Maheswaranathan, N., and Ganguli, S. (2015). Deep unsupervised learning using nonequilibrium thermodynamics. In International Conference on Machine Learning, pages 2256–2265. PMLR.
29. Sundararajan, M., Taly, A., and Yan, Q. (2017). Axiomatic attribution for deep networks. In International conference on machine learning, pages 3319–3328. PMLR.
30. Tsakiris, M. and Haggard, P. (2005). The rubber hand illusion revisited: visuotactile integration and self-attribution. Journal of experimental psychology: Human perception and performance, 31(1):80.
31. Yuan, Y. (2022). On the power of foundation models. arXiv preprint arXiv:2211.16327.
32. Yuan, Y. (2023). Succinct representations for concepts. arXiv preprint arXiv:2303.00446.
33. Zbontar, J., Jing, L., Misra, I., LeCun, Y., and Deny, S. (2021). Barlow twins: Self-supervised learning via redundancy reduction. In Meila, M. and Zhang, T., editors, Proceedings of the 38th International Conference on Machine Learning, ICML 2021, 18-24 July 2021, Virtual Event, volume 139 of Proceedings of Machine Learning Research, pages 12310–12320. PMLR.
本文来自微信公众号:集智俱乐部 (ID:swarma_org),作者:贾伊阳,编辑:梁金

