“三体”运动为什么不能精确预测？

本文内容整理自北京师范大学复杂系统国际科学中心刘宇老师的直播：动力系统分析：“三体”运动为什么不能精确预测？本文来自微信公众号：集智俱乐部 （ID：swarma_org），作者：刘宇，整理：董佳欣，编辑：邓一雪，原文标题：《如何预测混沌？从罗密欧与朱丽叶的恋爱动力学，到三体问题》，题图来自：视觉中国

动力系统研究系统的状态或性质在一套固定规则下如何更迭变化。当系统的初始状态与状态变化规则已知，理论上可得之后任一时刻系统的状态，但实际上由于对初始条件的测量存在误差，以及计算过程中对数值的约算，对系统状态的精准预测被画上问号。

本文试着回答以下几个问题：如何对动力系统进行分析？存在不可预测的动力系统吗？导致不可预测的原因是什么？希望帮助大家对动力系统有更深的理解。

一、恋爱动力学：罗密欧与朱丽叶的爱恨情仇

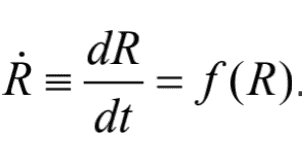
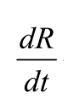
下面我们加入一个新变量J到系统中，给两个变量赋予含义，并且让他们之间产生互动，从而使我们的系统丰富起来。

我们假设此时爱可以量化， R表示罗密欧爱朱丽叶的程度，J表示朱丽叶爱罗密欧的程度，而他们双方爱意的变化遵从这个规则：

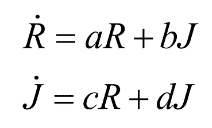
其中a、d、c、d为任意常数。

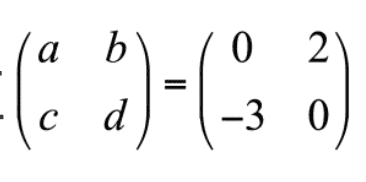
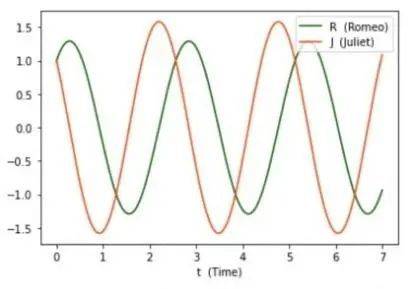
根据图我们不难发现，在这段关系中，一方的爱意大小会对另一方的爱意的变化产生影响，而如何影响是由a、 d、 c、d取值决定。针对上例中取值状况，我们若想进一步分析二人的爱意对对方的影响，不妨变换坐标，以R为横轴，J为纵轴，得到两人爱意动力系统的相图：

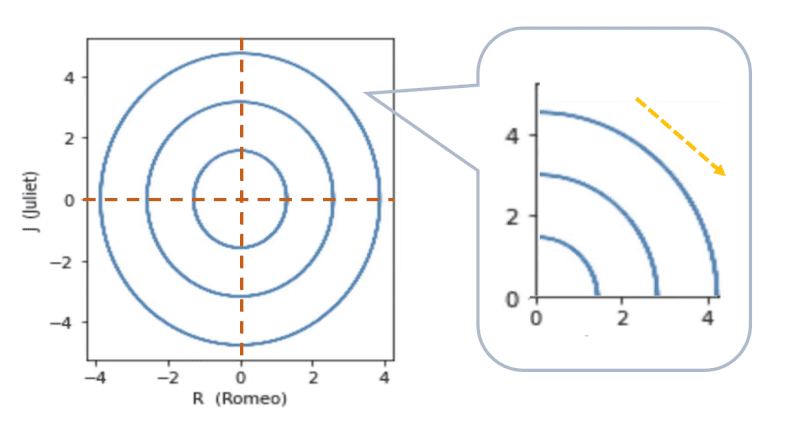
如何分析该图呢？我们取右上方区域放大，按黄色箭头方向来看，当罗密欧的爱意上升（横坐标变大）时，朱丽叶的爱意会下降（纵坐标变小），以同样的方法去分析另外三个部分，即可了解二人的爱意对对方的影响。

取不同a、d、c、d，会得到不同的双方爱意变化规则，如下图所示，再根据二人爱意的初始值，可得到之后任一时刻，两人对对方的爱意数值，并且根据两人爱意变化的规则，编出二人间不同的爱情故事。

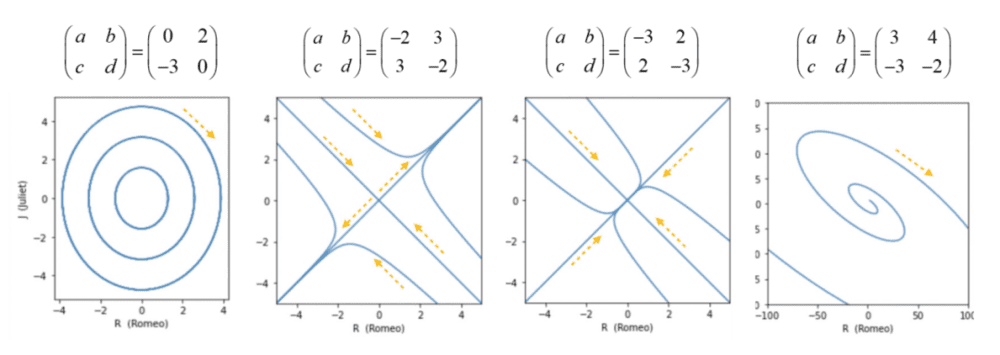
上述过程告诉我们，当系统遵循不同的变化规则，会使得系统相图呈现出不同样态，取不同样态间的共性，我们可以将相图根据其收敛方向、形态等特点进行分类，并根据系统相图所属的种类的特点，对该系统的发展有定性了解。

二、混沌：三体运动不能精确求解

现在，我们再给系统内加一个主体，并且让他们之间存在非线性关系，也就是变化规则中存在非线性项，这就进入到了所谓的“三体问题”，事实上这个问题早在几百多年前就被提出。

1885年，在刚创刊不久的瑞典数学杂志上出现了一则引人注目的通告：为了庆祝瑞典和挪威国王奥斯卡二世在1889年的六十岁生日，将举办一次数学比赛，悬赏2500克朗和一块金牌，比赛题目共有四个，其中第一个就是找到“多体问题”的所有解。而多体问题，又可追溯至 17 世纪晚期，当牛顿发现运动和引力定律时，牛顿定律非常清晰地阐述了行星轨道的形态。

乍看上去似乎只要应用牛顿定律，就能计算出任何一组相互间存在引力作用的物体的运动轨迹，可以是三体、四体或者任意数，只要知道起始状态，通过万有引力定律，一定可以把所有物体的任意位移计算到任意的精确程度。

庞加莱在读博士期间就已经开始研究太阳系中的多体问题，当他看到这则通告，毫不犹豫便选择了这个问题，他进展迅速，并完成以任意精度计算三体的运动轨迹，虽然这只解决了多体问题当中的三体情况，但仍征服了评委，得到这一赛事的奖励，且他的解答论文也被刊登在《数学学报》上。

不幸的是，很快他发现在证明的关键地方，忽略了数学函数的几何行为的一种微妙可能性，因此他对于三体问题的解答是错误的。庞加莱自费找回了已经被发放的杂志，并且更改了他的结论——从微积分的角度而言，万有引力影响下相互作用的三体问题没有可解析的积分解，这暗示着含有更多数目的多体问题也是无解的。

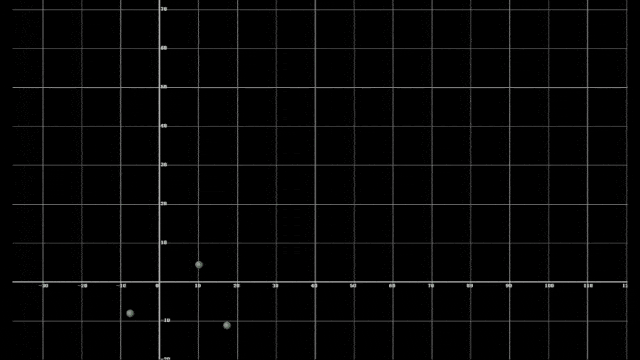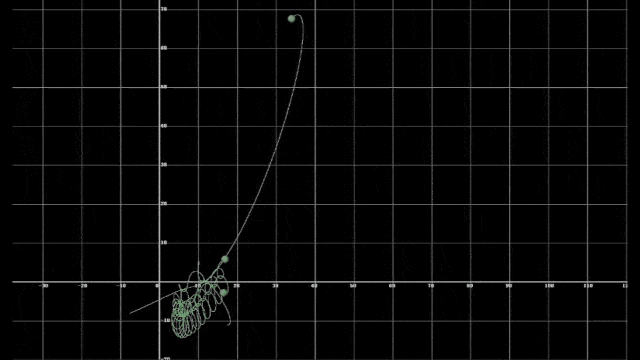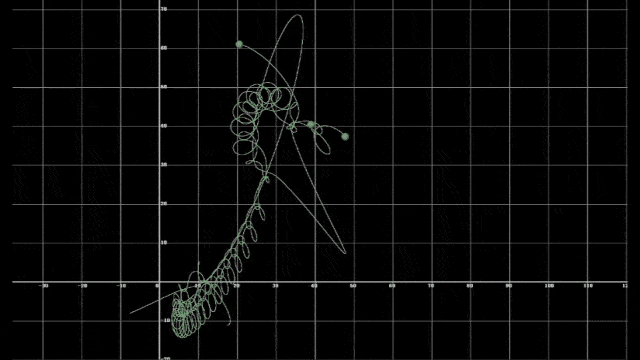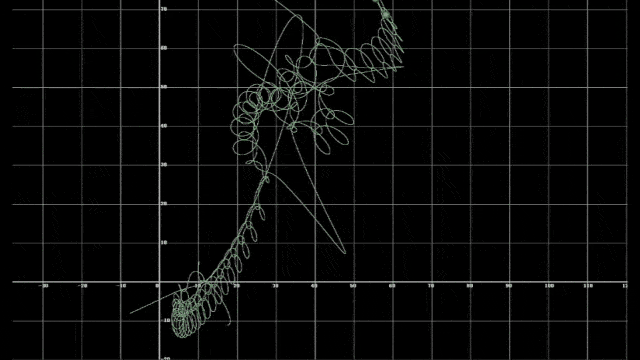
以上两视频展示了不同初始条件下的三体运动，可以直观发现它们的运动十分混乱、无序，且在某时刻会因为引力弹弓的原因被高速弹开。若用略为严谨的语言表述其之所以无法被预测的原因，是因为描述它们的方程无法涵盖和控制计算中细微的不确定性，即任何小数量级的误差都会导致全然不同的运动轨迹，这就是混沌的特性。

也正是因此，三体文明才会选择对地球发起战争，而不是发展科技预测三颗太阳的运动轨迹，因为任何观测或是计算上的微小误差，会导出极具差异性的运动轨迹，也就是摧毁了预测的能力。

三、蝴蝶效应：其实人家叫“对初始条件的敏感性”啦

混沌呈现出系统对初始条件的敏感性，即同一系统，在初始条件有细微差异的前提下，会导出两种完全不同的发展情况，其实也就是我们熟知的蝴蝶效应：一只蝴蝶在巴西扇动一下翅膀会在美国的得克萨斯州引起一场龙卷风。

拿洛伦兹系统来举例，如下面的动图所示，即使一开始两个点相距很近，以至于运动一段时间我们都看不出原来是两个点，但随着时间推移，两个点俨然开始走起各自的轨道，且两条轨道毫不相关，唯一的相似之处便是被限制在一定的运动范围内，而这个是该系统两个吸引子的影响。洛伦兹系统遵从的运动规则由以下三个方程决定：

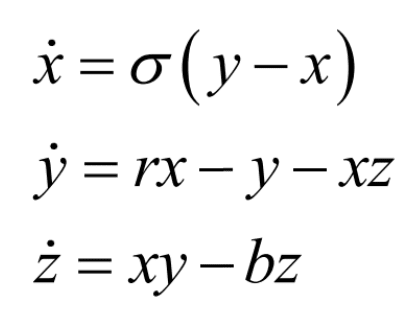
至于如何衡量一个系统对初始条件的敏感性，依靠的就是李雅普诺夫指数，它是用来描述两个点相互远离的速度。如下图所示的一个系统中的两条轨道：

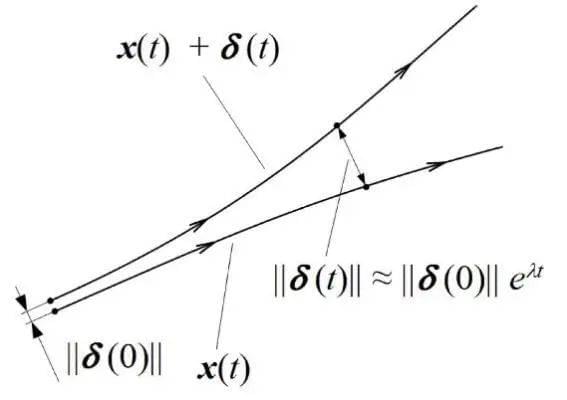
设初始时刻（t=0），两点的距离为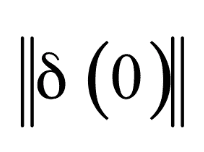，t时刻两点的距离变为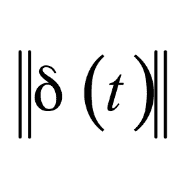，我们再令t时刻的距离约等于初始时刻的距离乘以一个随时间指数增加的值，即：

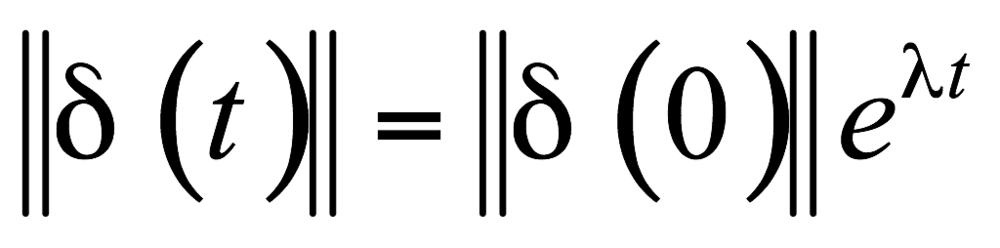
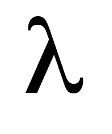
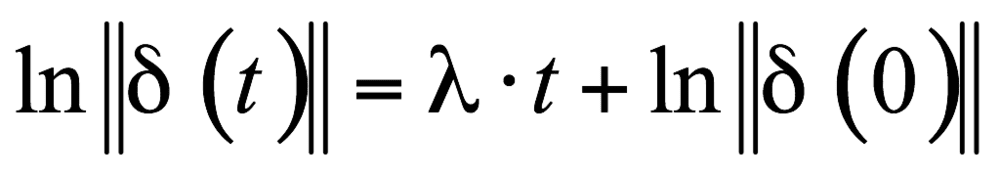
我们会发现该式的形式与直线的斜截式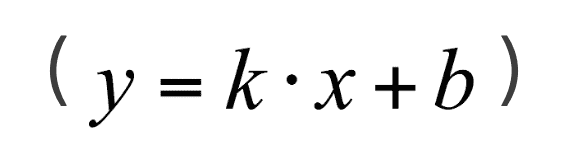、相同，所以此时我们得到的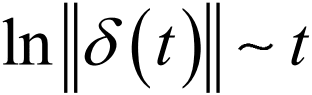图将会成为一条直线（如下图所示）。

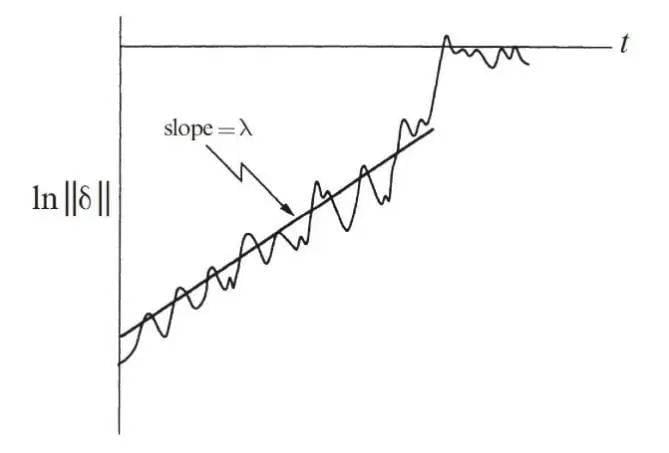
我们发现李雅普诺夫指数就是系统实际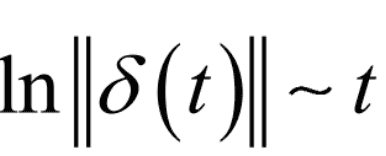曲线的近似直线的斜率，由此，我们便可以得到系统的李雅普诺夫指数。

同时，我们再回到定义李雅普诺夫指数的公式，会发现当其为正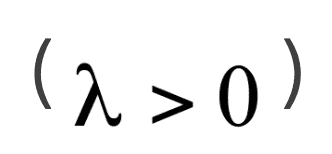时，因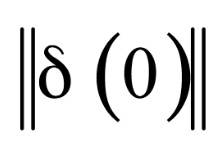

为一定值，故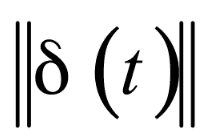会以指数速度增加，换言之，系统中两点会以指数速度分离，也就是进入两条毫不相关的轨道。

而对于系统是否存在动力学混沌，可以从最大李雅普诺夫指数是否大于零非常直观地进行判断——正李雅普诺夫指数，意味着在系统相空间中，无论初始时刻两点距离多么靠近，其间距都会随着时间成指数率的增加以致达到无法预测，这也就是我们所说的混沌现象，而李雅普诺夫指数的大小，暗示着两点分开的速度，也就是系统进入混沌状态的速度，或者也可以说系统不再能被预测的速度。

此时再回过头去看一些系统，根据其李雅普诺夫指数的大小，我们便能大致估计出对系统进行预测的程度。例如对于太阳系各行星运动，我们能预测到400～500万年左右，对于天气系统，我们能预测到15天左右，而对于混沌电路，则仅能预测1毫秒左右。

因此由于系统的非线性性质，部分系统将面临必然走向混沌的结果，故而我们不能仅通过观测其在某一时刻的状态与演化规律，就精确预测任意时刻后该系统的状态。因此，就无须抱有一些不切实际的期待，比如希望天气预报给出未来一个月的天气情况。

四、对于混沌的最新研究

正如前文所讲，多数非线性系统难以求解析解，因为相较于线性系统，它不能分成几个部分单独求解，并重新整合。但自然界的很多复杂系统，如气象变化、化学反应、病毒感染、人口移动、社会行为等，各部分会相互影响、合作或竞争，也就是出现很多非线性作用，因此学会用整体的目光，关注系统中的复杂性与偶然性就显得尤为重要。

混沌理论就是非线性科学中发展出的理论，它是关于系统从有序突然变为无序状态的一种演化理论，是对不规则而又无法预测的现象及其过程的分析。

然而，混沌不是纯粹的无序，而是不具备周期性变化和其他明显对称特征的有序态，因此该理论可以为我们研究自然科学或社会科学中诸多现象的不确定性做出解释与分析。与此同时，该理论延展出的如何控制或利用混沌现象的研究，还被应用于神经网络、非线性电路、天体力学、非线性机械故障诊断系统等诸多领域，向我们展示了其广阔的发展前景。

本文来自微信公众号：集智俱乐部 （ID：swarma_org），作者：刘宇，整理：董佳欣，编辑：邓一雪