本文来自微信公众号:返朴 (ID:fanpu2019),作者:邵城阳(芝加哥大学数学系博士后),原文标题:《〈三体〉最基础的那个设定,究竟有多不可预测?》,题图来自:《三体》
随着电视剧《三体》的热播,关于这个科幻故事背后的科学原理的讨论再次进入人们的视野。“三体问题不可求解”是对庞加莱的工作的通俗解释,它是整个故事最基础的设定。然而,纵观动力系统理论和天体力学的发展史,我们会发现,人们对于“可以求解”或者“不可求解”的认识发生过好几次剧烈的变化,今后当然也有可能继续变化。对于这些具体的问题作出论断,现在还为时尚早。
混沌理论所预测的“不可求解”现象,大大拓展了人们的思维。尽管只有一字之差,但它远远不等同于“不可理解”,也远远不意味着探索多体运动规律的努力走向终结。
从三体到《三体》
“星辰永不超越其界限(Nunquam praescriptos transibunt sidera fines)。”当庞加莱(Henri Poincaré)在论文《三体问题与动力学方程》的封面页写下这句格言时,他应该相当确定,自己“证明”了一个了不起的结论:
给定两个大质量天体和一个小质量天体,假定三者之间的相互作用符合万有引力定律,并且后者对前者的作用小到可以忽略不计。则这三个天体组成的系统是稳定的。
这正是大名鼎鼎的限制性三体问题(restricted three-body problem)。1888年,庞加莱将这篇手稿交予奥斯卡二世数学奖评选委员会,作为数学奖征解第一题的解答:
给定一质点系,其中质点的相互作用遵从牛顿(万有引力)定律,并假定任意二质点均不会相撞。将每一质点的坐标用时间的函数表示出来,要求表达式对任意时刻均收敛。
这正是有着悠久历史、在天体力学中占有基本地位的多体问题。出题者是委员会成员、近代分析数学的奠基人魏尔斯特拉斯(Karl Weierstraß)。魏尔斯特拉斯相信,只要足够精细,质点运动规律的明显表达式是可以得到的。竞赛要求参赛者匿名投稿,只在封面留下一句暗语以确认身份。庞加莱选择了“星辰永不超越其界限”这句野心勃勃的格言。他意图找到星辰所不会超越的界限——万有引力作用下天体运动的规律。更确切地说,他意图精确求解其中最为人熟知的限制性三体问题。

天文学家早已知道了太阳系内行星运动相当精确地遵从开普勒定律。翻译成数学语言,这表示:两个遵从万有引力定律的质点的运动,在质心系之下是非常规整的圆锥曲线(开普勒轨道)。但如果试图求解某个行星的卫星——例如月球——的运动规律,那么问题就立刻变得复杂起来,因为影响着月球运动的有太阳和地球两个大质量天体,还不算其它离得很远的天体造成的摄动。如果忽略月球自身的引力,而只把它当作地-日引力场中的质点,那么我们就得到了限制性三体问题的一个相当日常生活化的例子。
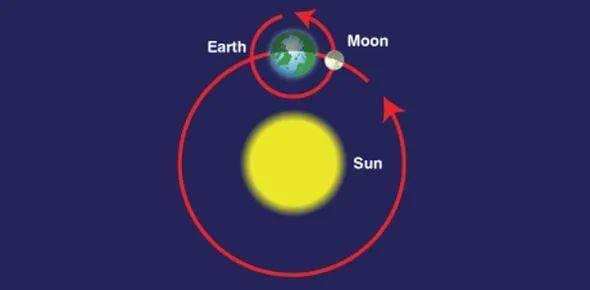
这些问题从牛顿的时代开始就已经在困扰天体物理学家了。而今,庞加莱似乎精确地解出了其中一个重要的例子,完成了几代天体物理学家的梦想;更重要的是,他引入了一系列重要的解析方法以分析天体的运动。这样看来,奥斯卡二世数学奖授予庞加莱,可谓实至名归;而这篇论文仿佛也将开启完全定量描述天体运动规律的理论革命。
回顾科学史,我们知道,庞加莱的确开启了一场理论革命,然而革命其实转向了与最初的预期完全不同的方向。如果没有庞加莱的工作开启的理论革命,天体物理学家们可能要晚很久才会认识到混沌特性——某种意义上,这表示运动规律很难精确求解——才是内禀于天体力学系统的,而这一支科学理论对大众文化的影响也会截然不同。果真如此,刘慈欣的科幻小说《三体》恐怕就需要一个完全不同的理由,让三体文明不得不抛弃母星、开始星际殖民。
“三体问题不可求解”是庞加莱成果的一种通俗说法。刘慈欣将它当作一条科学规律。他笔下的三体文明科学史,正是庞加莱故事的放大版本:野心勃勃的科学家们想要求解行星在三个太阳作用下的运动规律,然而经过一次又一次没能预测的乱纪元灾难,他们逐渐发展出相反的理论,最终证明了这个问题无法求解;生存得不到保障,于是走向星辰,走向与四光年外的太阳系勾心斗角的未来,走向母星毁灭的未来。
需要指出的是,按照物理学界通行的表述,刘慈欣小说中的问题其实不是“三体问题”,而是“限制性四体问题”,即研究小质量质点在三个大质量质点作用下的运动,忽略小质量质点自身的影响。显然,这里有四个质点。这问题当然比限制性三体问题还要复杂、还要混乱。不过,说科幻作品的科学基础“有硬伤”,并不能构成一个合理的批评。谁也不该要求虚构作品完全基于真实的设定。
不论看没看出术语问题,不论是否相信三体问题“不可求解”,都不影响欣赏作品,就好比信仰不影响欣赏其它民族的创世神话。但从科幻作品所基于的设定出发,重新审视我们所知的科学,却仍有可能得到一些教益。就让我们从庞加莱开启的混沌革命开始,来看看古老又年轻的三体问题。最重要的一点,我们应该把“三体/多体问题不可求解”——还需要明确什么叫“求解”——当作一条科学的铁律接受下来吗?
混沌革命
转折开始于委员会秘书弗拉格曼(Lars Phragmén,数学家,以复变函数论工作为人所知)对结果的疑问。弗拉格曼无法读懂庞加莱的全部论证,最终写信向庞加莱提出质疑。庞加莱在重新检查论文后发现了几处严重的错误。他重写了论文中错误的部分,重写的论文刊登在米塔-列夫勒(Gösta Mittag-Leffler)主编的杂志 Acta Mathematica 上。按照数学家伯克霍夫(George Birkhoff)的说法,这可能是 Acta 杂志发表的在科学史上最重要的论文。它开启了现代动力系统理论。
虽然庞加莱仍然保留了“星辰永不超越其界限”的格言,但这一次,他的论文却给出了与预期完全相反的结论:一方面,解的满足要求的形式级数表达式很可能不收敛;另一方面,实际上有如下的严格论断:限制性三体问题有很多相当混乱的解。
庞加莱研究的是如今称之为哈密顿系统(Hamiltonian system)的微分方程组。这种方程组开始于一个包含2n个自变量的函数H(q, p),其中q, p都是有n个自由度的向量,分别称为广义坐标和广义动量。方程组的一般形式是:
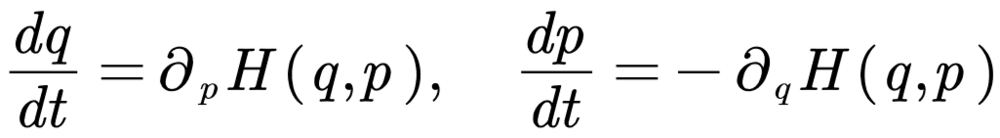
它所描绘的轨线定义在(q, p)所生活的2n维空间里。这个并不存在于现实中的空间叫做相空间(phase space),方程组的解则称为相流。
我们熟悉的许多经典力学系统都能够化成这种形式,只需要取q为通常的空间坐标,p为通常的动量就可以了,而这时哈密顿函数H(q, p)正是系统的总能量。它是一个守恒量。对于多体系统,除了总机械能外,总动量和总角动量也是守恒量。如果只有两个质点,这足以导出开普勒定律。要想求解多体系统的运动规律,自然要先看看还有没有别的守恒量。
庞加莱在论文中定义了他称为积分不变量(integral invariant)的对象,守恒量是其中的一种。在注意到相空间体积是积分不变量之后,庞加莱证明了第一个重要结果,也就是著名的常返定理(recurrence theorem):如果相空间中的等能量面都是有界闭曲面,那么对于相空间中每一个有界区域,不论多么小,都有轨线可与之相交无穷多次。对于多体系统来说,这表明相流不可能特别顺滑:轨线在相空间中总要时常“拐弯回归”。在末尾部分,庞加莱又证明了另一个重要结果:除了总机械能、动量和角动量这几个守恒量以外,多体系统再没有别的守恒量了!用今天的术语来说,多体系统是不可积(non-integrable)的。这粉碎了像二体问题那样用守恒量求解的希望。
论文中段的内容包含着庞加莱最重要的两项成果。我们先来看看跟相流的混乱特性直接相关的一项。通过选取合适的非惯性坐标系,庞加莱将限制性三体问题转化成了自由度为2的哈密顿系统。他引入了后世称为庞加莱截面(Poincaré section)的对象:在相空间中的等能量面上,这是一个所有轨线都与之横截相交的二维曲面,截面上的每一个点在演化中都会离开截面,而后再次与之相交。这个将曲面上的一点变为下一次相交点的映射,叫做庞加莱映射(Poincaré map,见下图)。
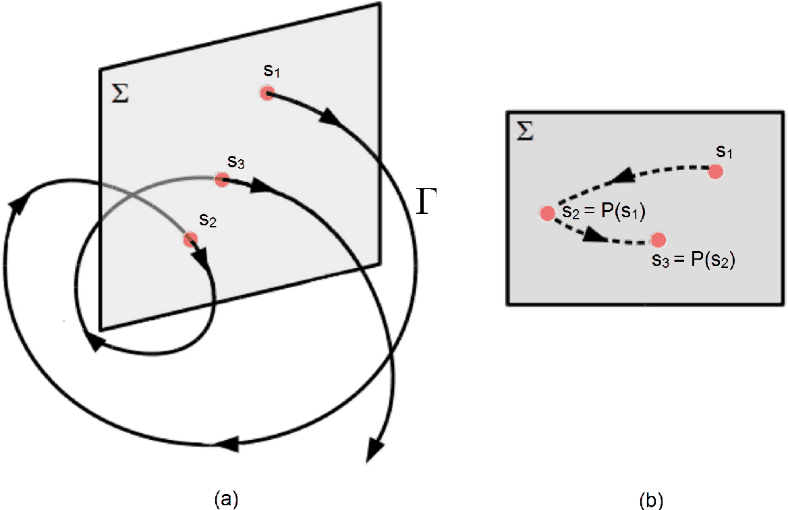
由此,研究相空间中轨线可以归结到研究庞加莱映射P。它的不动点O对应于力学问题的周期解。庞加莱引进了现代动力系统中称为吸引集和排斥集的对象:前者包含在P的迭代之下趋向不动点的那些点,后者包含在P的迭代之下远离不动点的那些点。
庞加莱发现,对于限制性三体问题来说,有相当一部分能量的取值,会导致相应的庞加莱映射产生奇怪的行为:它的吸引集和排斥集竟然会相交无穷多次。用今日的术语,这种交点叫做横截同宿点(homoclinic intersection,见下图)。如果回归轨线的性态,这种现象意味着:在周期解附近的轨线会无限多次地跑到离点O越来越近的地方,也会无限多次地远离它。

后世的动力系统理论指出了这种情况下的庞加莱映射P有多么混乱。
首先,在P的迭代之下,两个离得很近的点也会彼此远离。从数值求解的角度,这意味着,在这些区域里,哈密顿微分方程的解对初值的微小变化极端敏感,任何微小的误差都有可能被放大到难以接受的程度。
第二,在P的迭代之下,任何两个点都会无限多次地越来越接近,又会无限多次地相互远离。这意味着任意两条解曲线都会无休止地相互纠缠、远离。第三,在P的迭代之下,周期点构成截面上的稠密集合。这意味着微分方程又的的确确有非常多的周期解。一定程度上说,这足以粉碎“为限制性三体问题寻找好用的解析表达式”的天真愿望,毕竟没有哪种解析表达式会这么混乱。
这些特性后来被斯梅尔(Stephen Smale)于1960年代在另一个完全不同的场景中重新发现。他的学生德瓦尼(Robert L. Devaney)将上述三条特性分别概括为初值敏感、拓扑传递和周期点稠密,并将满足这三条特性的动力学现象命名为混沌(chaos)。李天岩和约克(Li and Yorke)的著名论文 Period Three Implies Chaos 则说明这种现象对于连续映射的迭代来说相当常见。自此,动力系统定性研究的时代开始了。
在混沌的诸多奇异特性中,初值敏感的特性比较容易理解,它很快随着洛伦兹(Edward Lorenz)早年发现的微分方程进入了大众文化,并获得了“蝴蝶效应”的雅号:“蝴蝶扇动翅膀,可能引发一场龙卷风”。然而,我们应该记得,这种现象最早是庞加莱发现的。可以说,庞加莱的工作开启了混沌革命。
遍历性疑难
庞加莱的工作迫使物理学家们大大修正自己的直觉。毫不夸张地说,从1920年代开始,在相当长的一段时间里,这种直觉摆向了另一个极端:相信一般的力学系统都相当地“混乱”。彼时还没有“混沌”这个概念,那么“混乱”在这里是什么意思呢?
让我们从一个简单的数学实验开始。考虑二维环面上的一个动点,它的经度和纬度都随着时间均匀增加,但增加的速率不同;假定两者的比例为ω。按照这个规律运动的轨线是什么样子?下图显示的分别是ω=5和ω=√2的轨线。可以看出,前者非常简单,而后者却密密麻麻,铺得到处都是。
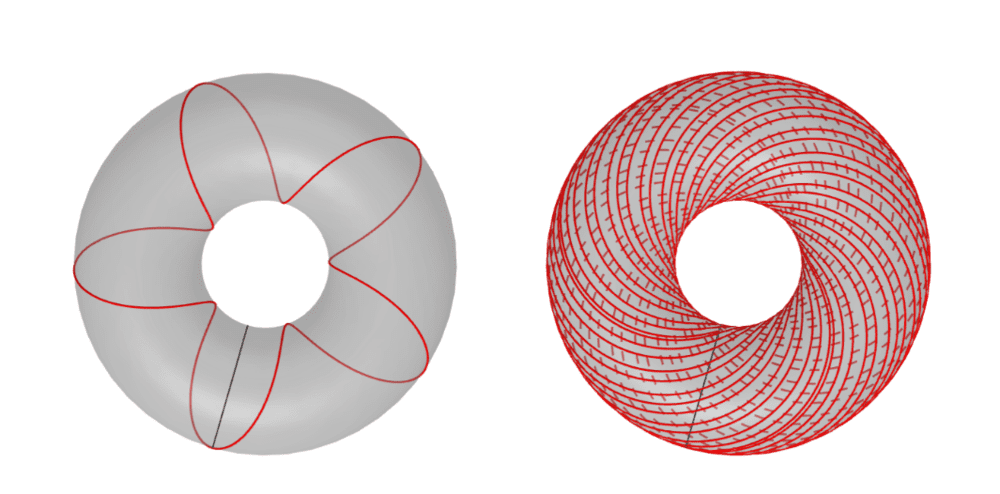
如果ω是有理数,那么轨线会绕着环面转几圈之后回到起点,转的圈数取决于ω的分母有多大。但如果ω是无理数,那么情况就要复杂得多了:轨线无论如何也不可能回归起点,而且至少根据我们的数值实验,它似乎要穿越环面上的每一个区域。实际上还会有更强的结论:给定环面上的区域Ω,则在Ω内部的轨线之长度占轨线全长的比例,会渐渐接近Ω的面积占整个环面的比例。
学过微积分的读者不妨试着将这个结论用极限的语言表达出来,并作出证明(提示:三角级数)。在现代数学术语中,这种“均匀地游遍全世界”的现象叫做“时间平均等于空间平均”——遍历性(ergodicity)。这个概念最早由物理学家玻尔兹曼(Ludwig Boltzmann)在1870年代研究统计力学时提出,而将其定义严格数学化的,正是前文提到的高度评价庞加莱工作的伯克霍夫。玻尔兹曼提出了遍历性假设:一般的统计力学系统都有这种“时间平均等于空间平均”的性质。
在具有遍历特性的动力系统中,个别点的轨道无疑可以称得上混乱,尽管这种混乱与“混沌”其实相当不同——虽然混乱,但仍然可能有规律可循。刚刚举出的环面上的例子就是如此:虽然轨线散布得到处都是,但却有明确的表达式,包含的只是像:
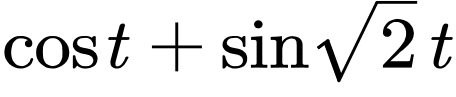
这样的函数。学过电子信号的利萨如图形的读者,对这种函数应该不陌生。它属于所谓的拟周期函数(quasi-periodic function)之列。形式上来讲,拟周期函数比周期函数复杂一些:它可以有多于一个基频,如果将基频记作向量ω=(ω1,…,ωn) ,则拟周期函数就定义为:
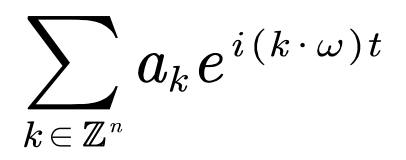
后面会看到,拟周期函数将扮演非常重要的角色。
玻尔兹曼针对的是有着巨量粒子的系统,而庞加莱所证明的常返定理却提示说,“简单”如三体系统的哈密顿系统,也可能会“均匀地游遍全世界”。物理学家们由此开始相信,一般的哈密顿系统也会有这种混乱的遍历性质。费米(Enrico Fermi)正是一个严肃对待这一假设的物理学家。
在1923年,费米发表了一篇文章,试图证明如下结论:在庞加莱常返定理的假设之下,哈密顿系统在相空间中的等能量面上是遍历的。尽管当时这被物理学家广泛地接受,而且还有不少数学上的证据侧面支持这个猜测(例如伯克霍夫的个别遍历定理),但他的“证明”其实是不对的——不是物理学家所熟悉的“数学上不严格”,而是我们后来知道这个结论本身是错的。
然而我们不该由此苛责古人。费米不愧是伟大的物理学家,他虽然给出了“证明”,但仍然相信物理直觉需要经过实验检验。在1950年代,费米小组开启了一项数值实验,用著名的MANIAC I计算机(它是第一台在棋牌游戏中击败人类的计算机)演算了两个包含64个粒子的力学模型。它们如今被叫做FPUT模型(Fermi-Pasta-Ulam-Tsingou model)。
费米小组原本期望能够通过数值演算观测到很强遍历特性,然而结果却令他们感到惊讶:所有的解最终都变得非常“规律”——数值结果显示,它们最终都越来越接近上文提到的那种拟周期函数。虽然也算得上有遍历特性,但程度却远远称不上混乱。研究小组在1955年的报告中失望地总结道:“计算结果几乎没有显示出任何趋向能量等分(注:等能量面上遍历性的推论)的可能性。”
这种境况完全可以叫做“遍历性疑难”了:实验结果和理论直觉完全不符。从今人的视角来看,我们可以这样解答疑难:在常返定理和遍历性质、乃至完全的混沌之间,还有着许许多多的可能性。庞加莱的工作,在一定程度上导致了矫枉过正,让学者们在相当一段时间里忽视了其它的可能性。
绝处逢生:KAM
其实,从最基本的常识出发,要找出能够说明遍历性疑难的例子再简单不过了:为什么我们能够看见太阳和月亮日复一日地、稳稳当当地东升西落,而不是像三体世界里那样混乱到不可预测?按庞加莱的研究成果,“理论上”来讲,三体系统的解“有可能”相当不稳定,那么为什么高悬的日月恰好就没有处在这种可能之中呢?
一个直接的解释是:我们所处的太阳系可能具有混沌特性,但是混沌特性却也未必意味着星球会到处乱飞,而可能只是体现在公转相位上的混乱;另外,以人类的观察尺度,不稳定性可能需要相当长的时间才能够体现出来,我们很难直接察觉到。总之,它的混乱不像《三体》小说中那样,暴烈到能轻易毁灭上千轮的文明。
这种“混乱但温柔”的解释很好地平衡了理论与常识,而且也有越来越多的天文学证据支持这种解释。然而,仔细想来,它其实巧妙地绕开了我们关心的核心问题:一般的哈密顿系统到底有没有遍历特性?
如果站在1954年就去世了的费米的角度,问题的答案恐怕相当出乎意料:有很多一般的哈密顿系统虽然不可积,但却并没有遍历特性。这个回答主要归功于三位重要的数学家:柯尔莫戈洛夫(Andrey Kolmogorov)、阿诺德(Vladimir Arnold)和莫泽(Jürgen Moser),他们的系列成果因此简称为KAM理论。
问题其实仍旧开始于庞加莱的论文。为了研究限制性三体问题的解是否有收敛的级数表达式,庞加莱试着将第三个质点的质量当作微扰参数,将解展开为时间的三角级数。翻译成数学语言,这是要寻找哈密顿函数h0+h相流的拟周期解,其中h0有着可精确求解的、可积的相流,轨线是拟周期的;而h则是一个“小扰动”。由于h可以是随便什么函数,h0+h可以说是非常“一般”的,自然不会给出可积系统。对于恒星-行星-卫星问题来说,h0就是忽略掉卫星同恒星的相互作用的哈密顿函数,其拟周期解对应的就是行星和卫星的开普勒轨道;而h由于正比于卫星的质量,从而可以视为微扰,但它破坏了可积性。
这种级数最早是林德斯泰特(Anders Lindstedt)开始考虑的,但庞加莱在研究时立即发现了一个问题:林德斯泰特级数在这里的表达式形如:
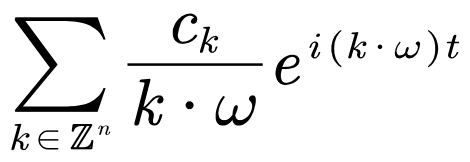
其中ω=(ω1,…,ωn) 是微扰前解的振动频率。这是一个拟周期函数。为了这个表达式不出问题,就得要求频率向量ω是有理无关的——它的分量的有理线性组合不能为零。然而即便如此,作为分母的k·ω仍然有可能非常小,这就可能破坏级数的收敛性。非常奇怪地,它能小到什么程度是一个纯粹的数论问题,在数论中属于丢番图逼近(Diophantine approximation)这一分支。
庞加莱的时代尚没有处理这种问题的工具,因此他在论文中只得猜测:林德斯泰特级数“非常有可能”发散。鉴于论文已经证明了三体系统在某些能量曲面上的混沌特性,猜测林德斯泰特级数发散是很有道理的——不应该期望它真的能给出我们想要的解。然而随着数学工具的发展,这种尝试居然绝境逢生了。
实际上,类似的问题在一个看似遥远的数学分支——复变函数论里也出现了。人们关心这样的问题:一个复解析函数f(z)=λz+O(z2)在z=0附近的迭代,能否通过适当的解析变换,变成其线性部分z→λz的迭代?如果要将解析变换展开成z的幂级数,那么也要碰到类似的小分母问题:这里作为分母的是序列λn-λ。如果λ=eiθ,其中θ与π不可公度,那么分母序列永远不会等于零,却仍旧有可能非常小。
为了所求的幂级数收敛,数学家西格尔(Carl Siegel)给角度θ额外附加了所谓丢番图条件,要求它不能被有理数太好地逼近。在这种限制之下,西格尔证明了如下定理:只要θ满足丢番图条件,就能够找到满足要求的、接近于恒等变换的解析变换。
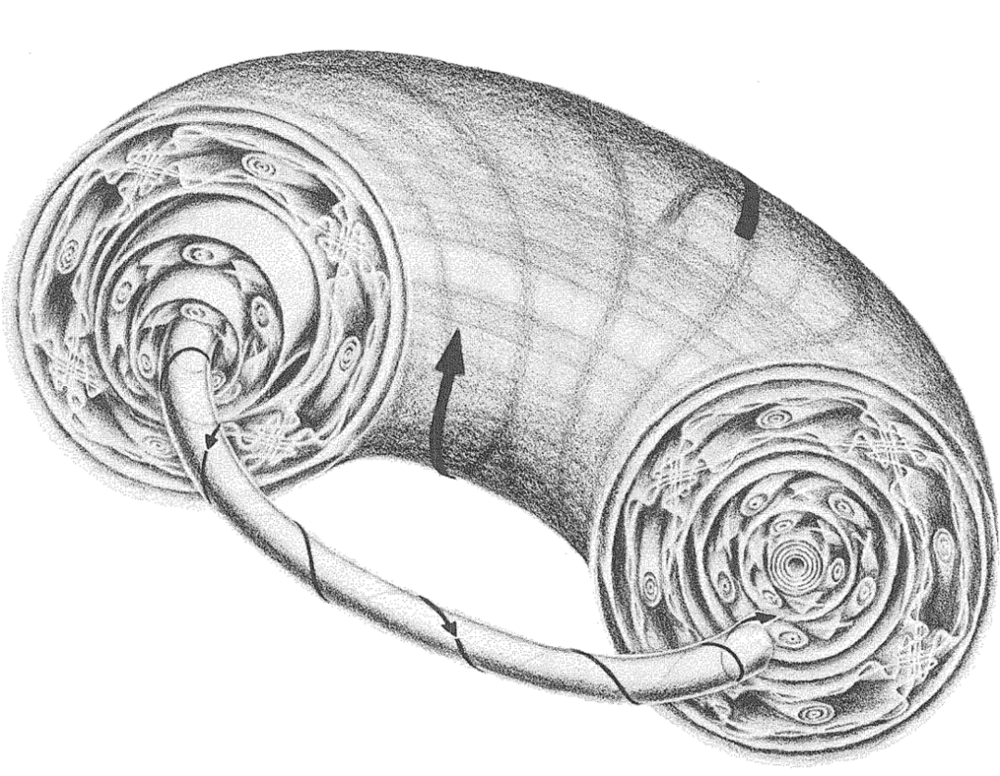
西格尔的工作完成于1940年代。虽然没有明确的历史证据,但他的工作可能启发了科尔莫戈洛夫。科尔莫戈洛夫开始真正考虑哈密顿函数为h0+h的相流的微扰问题。这个问题可以说是开普勒轨道微扰问题的抽象版本:假定有某种合适的正则坐标,使得相空间中的点可以改用“相角”x(每个分量都有周期2π)和“作用量”y来标记,而函数h0=h0(y)只依赖于y;这种情况下,h0的相流就可以精确求解为:
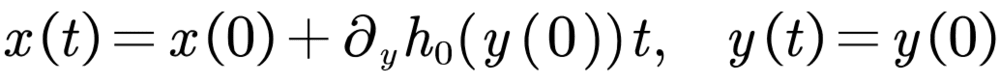
因此, h0的相流中所有的轨线都必定落在相空间里的某个环面h0(y)=常数上(见下图),而只要频率向量:
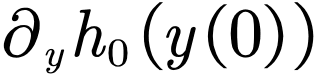
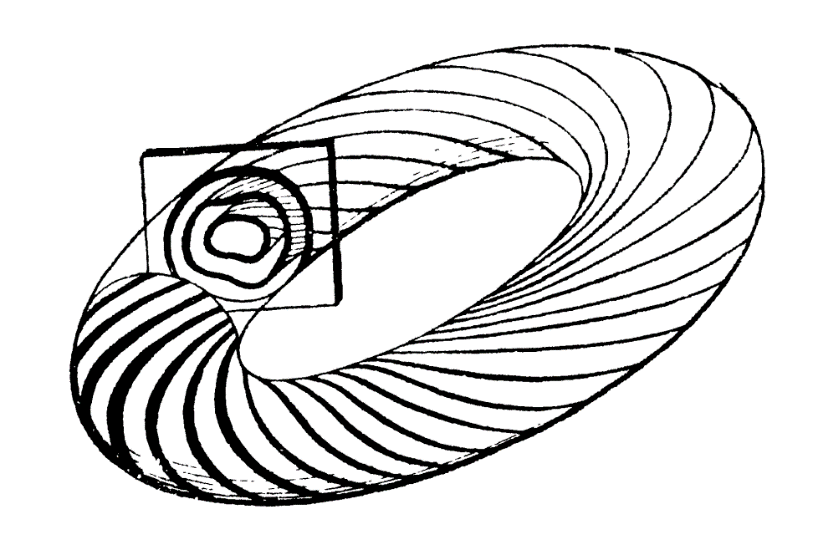
现在的问题是,在加上扰动h之后,有没有环面不至于破裂而是保留了下来呢?换句话说,扰动后的哈密顿函数h0+h还有没有拟周期的轨线呢?
这个问题当然比西格尔处理的问题更加复杂,但是在这个时代,技术上的困难已经难不倒数学大师科尔莫戈洛夫。他使用了一套本质上是牛顿迭代的办法,在每一步都找到一个能够接近于恒等变换的正则变换:
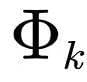
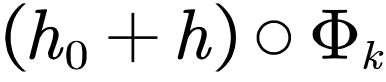
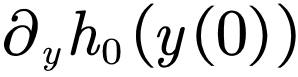
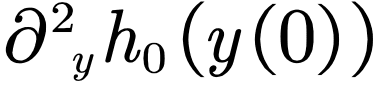
科尔莫戈洛夫其实没有完整地证明这个结论。第一个给出完整证明的人是他的学生阿诺德。莫泽从两人的工作以及纳什(John Nash)的工作里汲取灵感,将迭代方法抽象出来,成为了现代分析数学中一套强有力的方法,即所谓的 Nash-Moser 定理。KAM 理论极大地推动了分析数学里许多分支的发展,可谓是分析数学辉煌的篇章。
总之,出乎费米(以及同时代的许多物理学家)意料的是,一般的哈密顿系统其实并没有那么“混乱”——被扰动的可积系统不会满足遍历性假设。这种系统的轨线尽管复杂,却有很可观的部分被限制在相空间里的低维环面上,在很大程度上是可以预测的。这跟那种“混沌得出奇”的情景还是不一样的。
星辰之限
那么,既然有KAM理论作保证(虽然这属于后见之明),为什么庞加莱还是能够发现混沌现象呢?这其实是因为这两种理论的适用范围完全没有交集。KAM理论适用于相空间里这样的一些区域:扰动h的大小与h0相比很小。但在庞加莱所讨论的限制性三体问题里,第三个天体被假定具有比较大的机械能,几乎接近能逃逸大质量天体引力的水平,这远远超过了KAM理论起作用的范围。所以,KAM理论所保证的“小能量”下的稳定性,与“较大能量”之下出现的混沌特性之间并不矛盾。
这样一来,就出现了一个很有意思的问题:KAM理论能适用的范围到底有多大?特别地,能大到覆盖太阳系中的天体运动吗?
阿诺德提出了这样一个定理:对于有一个大质量恒星和许多黄道面几乎共面的行星的系统来说,KAM定理能够保证它们的开普勒轨道在扰动之后仍有一定概率是拟周期的。理论上,这似乎是太阳系稳定性的有力保障。可惜,在最早的版本中,KAM型定理所要求的微扰的尺度都小得出奇,远远小于天体之间质量的比例。另外,更本质的问题在于,许多重要的天体运动问题的哈密顿函数远远不满足科尔莫戈洛夫要求的非退化条件。
不过这些“理论上的”成果却足以提示我们:在许多可以视作微扰问题的情境里,KAM理论的机制尽管未必能够保证拟周期解的稳定性,却暗示这种稳定性是可以预期的。例如,在太阳-地球和月球组成的三体系统里,月球公转轨道同地球黄道面的夹角仅有5°左右,非常接近于三星共面的三体系统。虽然没有任何已知结果能够保证这个系统的稳定性,但KAM理论的存在却暗示我们,有一定可能证明它的稳定性。对于整个太阳系来说也是如此:这个系统稳定或不稳定的断言都各有证据支持,现在还远远没有到最终下决断的时候。
另外,KAM理论的某些改进版本也能够给出一些天体力学上的推论。例如,在2003年,Celleti和Chierchia就证明了太阳-木星-凯神星的限制性三体系统适合KAM型的结论,从而扩展了KAM理论的适用范围。从实际的角度来说,这表明:作为小行星一员的凯神星的轨道是很稳定的,尽管有木星巨大的引力所引起的摄动,它也并不会突然偏离原有轨道横冲直撞。他们的证明是由计算机辅助完成的,因为计算微扰级数的工作决非人力可及。
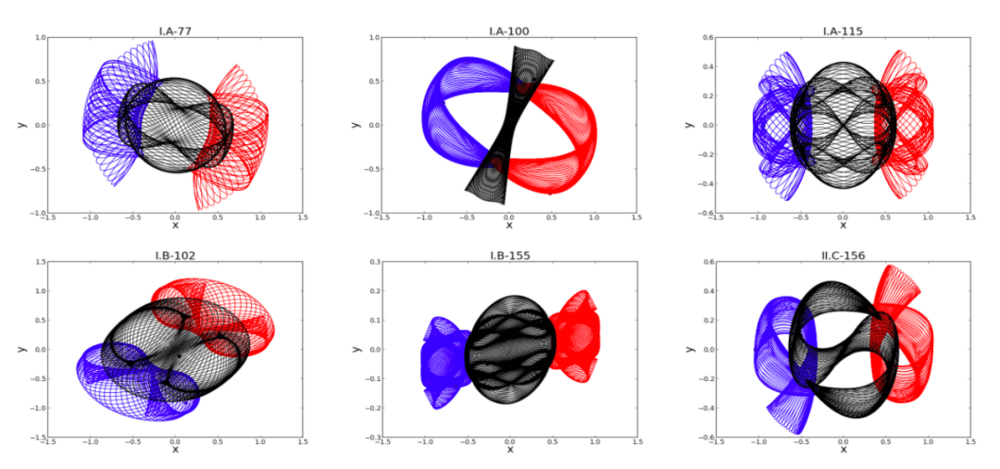
实际上,人们也已经开始借助计算机去寻找三体问题的特解了。例如,在2017年,上海交通大学廖世俊研究小组得到了等质量三体问题的695族周期解(见下图),此后更是将数量扩展至1349族和135445族。《三体》小说中,地球三体组织中有一派将求解三体问题作为向“主”表达爱戴的仪式,在故事中,作为局外人的魏成“取得突破”,找到了上百族解,激起了地球三体组织的内讧。看起来,作者为小说所虚构的研究成果,在计算机技术的实际进展面前已经有些落后了。
当然,人们可能暂时还没办法更深入地研究这些周期解的稳定性。不过,这些进展都提示我们,三体问题本身是非常复杂的:这里的“复杂”不是指绝对不可近似求解、不可预测,而是指它的解可能有许多种截然不同的表现:其中有些“混沌”的解会导致不可近似计算、不可预测;有些尽管“混沌”,却因为时间尺度太大的原因而仍然可以预测;而有些虽然复杂,却并非不能精确地求解。庞加莱证明的是“三体系统不可积”和“三体问题在某些能量区域展现混沌特性”,由此就作出“三体问题不可求解”的结论,其实有些粗疏。
距离庞加莱写下那句格言已经过去了一百三十多年。在这些年间,人类对于天体运动规律的认知经历了好几次剧烈的变化。我们有充足的理由相信,我们对这些规律的认识还远远不足,现有的认识框架也很可能会再次被颠覆。二十世纪里计算机技术尚不发达的时候,数理科学家就已经想到了别的办法去描述限制性三体问题在混沌区域的表现。尽管这些描述只是进一步揭示它在混沌区域的不可预测性,但谁知道人类将来能不能找到全新的认识框架,从而重新定义“可以预测”这件事呢?
星辰的界限是无穷无尽的,它需要两种非凡的勇气才能探索。面对复杂的境况,要有勇气直呼其名。为了直呼其名,则需要不断使用新的技术、新的语言,发展新的思维方式,而这就需要另一种勇气:准备好与习以为常的直觉决裂。
尾注:《三体》小说中提到的三体问题本身未必处在混沌的区域里。也就是说,这三颗恒星本身的运动未必会复杂到完全不可预测。实际上,真正不可预测的乃是那颗行星的运动。人们尚不知道,对于三颗恒星来说,限制性四体问题的混沌区域究竟在哪里?它本身又是否有稳定的区域,或者KAM理论能够应用的区域?这样看来,有三个太阳的行星是否可能有宜人的环境——与人类熟悉的地球环境相接近——其实是一个非常开放的问题。对科幻小说的设定较真,未必是抬杠。
本文来自微信公众号:返朴 (ID:fanpu2019),作者:邵城阳(芝加哥大学数学系博士后)

