本文来自微信公众号:返朴(ID:fanpu2019),作者:曹则贤,题图来自:视觉中国
一、引子
笑话年年有,今年更独特。近些日子,有中国台湾某退休将领,做电视节目嘉宾时言道:“一发导弹拦截的成功率是70%,那我三发一起拦截,成功率就是210% 嘛,哪有拦不住的!” 有点儿常识的人瞬间捕捉到这是个大笑话,吓得赶忙捧腹扶眼镜。
这笑话在华人圈一时间热度飙到42℃。有人直言这位退将的数学是体育老师教的,结果因为侮辱了体育老师被体育老师给打了。有女嘉宾怒怼,“一发导弹拦截成功率70%,三发拦截成功率就是210%,照这么说四杯25℃的水,倒在一起直接就沸腾喽!”还有人从排列组合的角度,分别给出三发导弹中与不中八种不同组合的概率。这画风转换有点儿快,一个笑话竟然还引出一堂数学课来了。
既然有人关切,笔者也来凑个热闹,假装很不严肃地好好讨论一下这个问题:“设一发反导导弹对来袭导弹的拦截成功率为70%,那么,三发一起拦截的成功率是多少?”
二、概率的数学初步
首先,alas,这个问题是错的!对着来袭导弹发射一发反导导弹,结果就两种:击中或者没击中。用数值表示,就是1或者0,没有成功率70%的说法。
所谓的成功率为70%这种说法,是一种统计语言的描述,而统计是针对大数而言的。设用某型号导弹拦截某确定型号的来袭导弹,在相同条件下实验了N次,其中成功了M次,则若N 足够大,数值
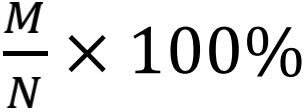
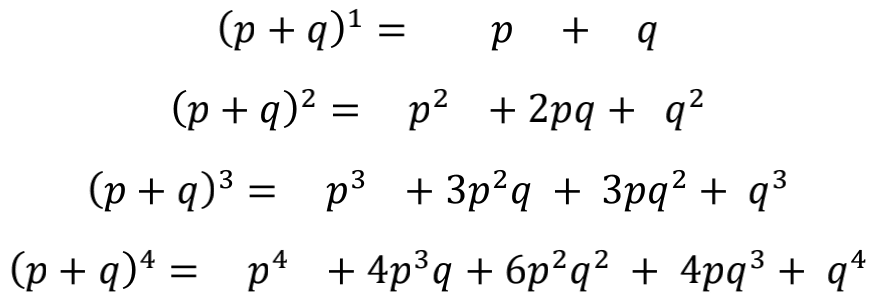
注意右面各行的系数。再硬性(!)引入(p+q)0=1 (这说明为什么自然数要从0开始), 就构成了大家熟悉的杨辉三角 (图1) 。
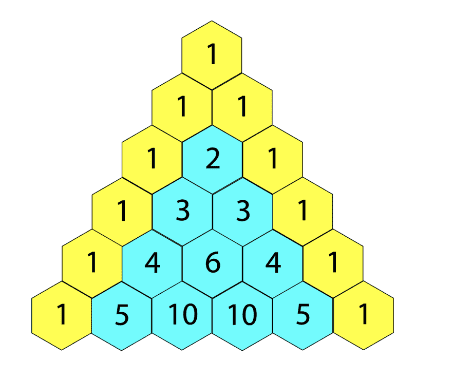
设想 p 是某件事发生 (成功) 的概率,q 是某件事未发生 (不成功) 的概率,p+q=1。现在神奇的事情发生了。不管 n 是几,(p+q)n=1都成立。这就是说,杨辉三角的每一行恰恰就是这类事件被重复考察n次时,相应的各种可能对应的概率。比如,对某事件实验三次,则表达式 (p+q)3=p3+3p2q+3pq2+q3 的右侧分别就是发生3,2,1,0次的概率;若对某事件实验四次,则表达式 (p+q)4=p4+4p3q+6p2q2+4pq3+q4 的右侧分别就是发生4,3,2,1,0次的概率。是不是很简单?
于是,关于“一发导弹拦截成功率为70%,三发导弹拦截的成功率是多少” 这事儿,有人会计算如下。参照表达式 (p+q)3=p3+3p2q+3pq2+q3 ,则三发皆中的概率为70%×70%×70%=34.3%,两发中一发未中的概率为3×70%×70%×30%=18.9%;一发中两发未中的概率为3×70%×30%×30%=44.1%。 三者相加,故拦截成功的概率为97.3%。或者, 拦截不成功的概率为 30%×30%×30%=2.7% ,则拦截成功的概率为100% -2.7%=97.3% 。简单吧?
三、导弹拦截拦截是个物理问题和经济问题
问题要是那么简单就好喽。
学过概率论的人都知道,概率论是一门坑很多的学科,要不天下有开赌场致富的非法路径呢。概率论不是简单的拿个算式去算个数,要考虑问题的物理图像,物理图像,物理图像!
先说说中学物理里的常见的接灯泡问题(伪物理问题)。设有一种灯泡,接上电会亮的概率为 p=70% (按说就不该出厂),问三个灯泡串联和并联的情形下(图2),教室有亮光的概率各是多少?如果是串联,有一个不亮就把整个电路断了,所以教室被照明的概率是表达式 (p+q)3=p3+3p2q+3pq2+q3 右侧的第一项,为34.3%;如果是并联,但凡有一个灯泡是亮的就行,所以教室被照明的概率是表达式 (p+q)3=p3+3p2q+3pq2+q3 前三项之和,也就是 1-q3 ,为97.3%。
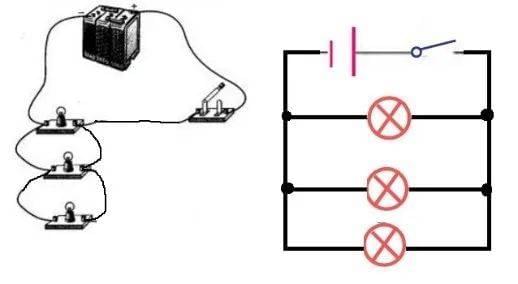
三个灯泡并联的问题, 与使用大炮轰击一个目标的问题相同:三发炮弹齐发,但凡有一发轰击到目标,即算达到目标。目标被摧毁的概率可以按照前述算法计算。这里计算正确性的保证来自三发炮弹的独立性。然而,关于三发导弹拦截一发来袭导弹成功率的计算,看似与三个灯泡并联和三发炮弹齐发的问题相同,但实际上却有很大的差别。
设若敌方有一发导弹来袭,且来袭导弹在飞行途中,这时的反导大概就是所谓的中段反导。若时间还允许,拦截方式大概是发射一发,如果成功,事情到此为止;如果不成功,赶紧补发一发。为什么不三发齐发呢?因为反导导弹太珍贵了,糟蹋不起。再者,导弹都是在高速运行中的,三发齐发又不能做到同时击中来袭导弹,则若一发击中来袭导弹(这是我们的追求和目标),其它两发不是白浪费了。这又不是炮弹轰击敌阵地,一发击中,补中两发算是加强打击效果。当然了,实际测试反导导弹性能时,双发齐发倒是真有的。三发齐发不是原则上不可以,而是实在没那么豪气。
如果敌方来袭导弹已经接近目标,这就是末段反导了。这时候的拦截务必要做到万无一失,特别是为了保护高价值目标,为此可以不惜代价。这个阶段的拦截手段一般使用近防炮。近防炮要形成一道动态的弹幕,让一段时间内的来袭目标,哪怕是一发炮弹,都不能通过。为此,近防炮的关键指标是射速,一般在每分钟6000发以上。我国新型船舰上使用的1130近防炮,射速超过每分钟一万发以上,射击距离在3公里左右。一分钟一万多发,速射十分钟就是十多万发。十万发速射炮炮弹,你估计一下得多少钱?真打不起啊。
四、来自反导的开悟
在基础物理中,描述一个运动物体,要用到质量 m,速度 v(这是一个矢量),动量 p=mv (矢量), 和动能 Ek=½mv2 。按说,有了质量 m 和速度 v 就够了,为啥还要用到动量和动能呢?关于这个问题,笔者当普物老师时没想明白,但是盯着导弹和反导的示意图(图3)时我想明白了。

首先,不管是导弹还是反导导弹,速度是硬道理。飞得够快,才能追得上对手或者免于被对手追上。这就是我们的导弹追求高速的道理。据公开信息,我国东风17的速度约为10马赫,东风41的速度可达25马赫,这速度是杠杠的。然而,导弹的高性能不光在于速度,还在于高机动性。导弹在突袭或者反导的时候要能灵活地变轨,这要根据牛顿第二定律,
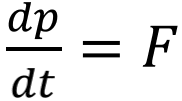
,其中力F由推进剂提供,可见动量是相关的物理参数。注意,对于速度在10 马赫量级的导弹,其不仅没有战斗部,在进入大气层后它还会因为高速飞行被逐步烧蚀掉,所以导弹的质量很关键。发射时质量要足够大,等到达目标时我们希望其还能剩个1公斤左右。接近目标后,导弹的毁伤能力则由动能表征。大家不妨计算一下一个1公斤的导弹头 (就是一块金属钨),速度为25马赫时,动能是多少?这样大家对它的威力就心里有数啦!
五、多余的话
那位退将侯的概率论水平,有点可笑,但并不可怕。笔者遇到稍微深一层面的概率问题,比如条件概率,就大概率会立马出错。真正可怕的是,“退将侯”这种水平的人是怎么当上将军的,是怎么能上电视节目给别人分析问题的?21世纪,国家发展问题首先是个科学问题,军事问题也首先是个科学问题,对此,我们要端正态度。
参考文献:曹则贤,军事物理学, 上海科技教育出版社 (2022).

本文来自微信公众号:返朴(ID:fanpu2019),作者:曹则贤

