本文来自微信公众号:集智俱乐部(ID:swarma_org),作者:陈关荣(香港城市大学电机工程系讲座教授、混沌与复杂网络研究中心主任;欧洲科学院院士;任《国际分岔与混沌杂志》主编),编辑:邓一雪,原文标题:《从哥尼斯堡七桥问题谈起丨陈关荣》,头图来自:视觉中国
有时候一句谚语或一个故事,便可以让许多人知道并记住一座城池。“条条大路通罗马”“拿破仑遭遇滑铁卢”“刘备借荆州”等,都是耳熟能详的例子。
哥尼斯堡之所以出名,或可归功于它那有趣的“哥尼斯堡七桥问题”。
一、哥尼斯堡七桥问题
哥尼斯堡(Königsberg)是座小巧玲珑的古都,位于欧洲波罗的海东南沿岸的桑比亚半岛南部,面积约1.5万平方公里,今天人口不到50万。该城堡由条顿骑士团(Teutonic Order)北方十字军于1255年建立,先后成为条顿骑士团国、普鲁士公国(Kingdom of Prussia)和东普鲁士国(East Prussia)的首府。
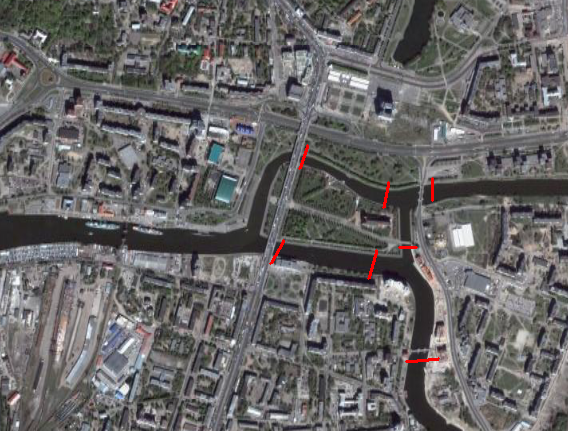
故事从流经市区的Pregel河讲起。这条小河在市区内有一个小岛,河面上有七座小桥(图2)。在18世纪,当地居民聊天时会经常讨论,是否可以从某一个地点出发,走过所有七条小桥,不重复也不遗漏,最后回到起点?
问题挺简单的不是吗,在纸上或地上画画不就画出来了?
没想到不少人画了很多个方案都不成功:绞尽脑汁,就是无法找到答案!
这时候,瑞士裔俄罗斯数学家欧拉(Leonhard Paul Euler,1707年4月15日-1783年9月18日)出场了。虽然没有记录表明欧拉亲自去过哥尼斯堡,但是当年七桥问题在民间流传很广,身在俄罗斯圣彼得堡的他知道了这个坊间游戏。年轻的欧拉对有趣的事物充满好奇心,居然认真地去思考这个小小问题。
1735年8月26日,欧拉向圣彼得堡科学院作了个学术报告,从数学上论证了:哥尼斯堡七桥问题是没有解的。
这里, 我们用今天大家熟识的语言来描述一下欧拉当年的推证。
首先,欧拉把城市的地图(图2)抽象为一幅数学的图(图3)。
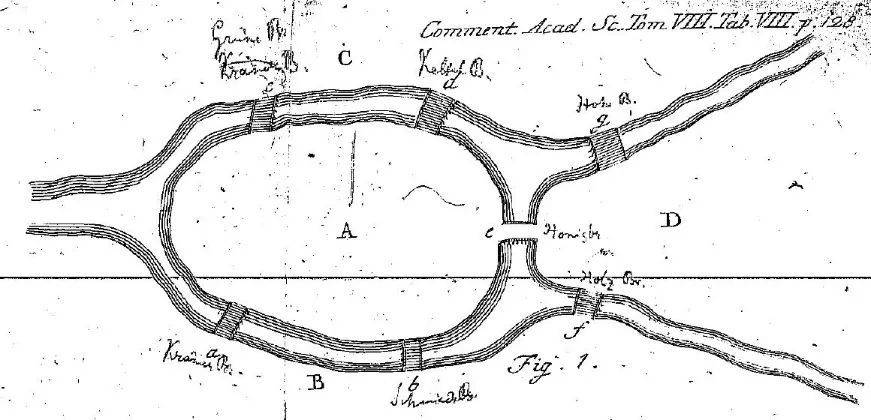
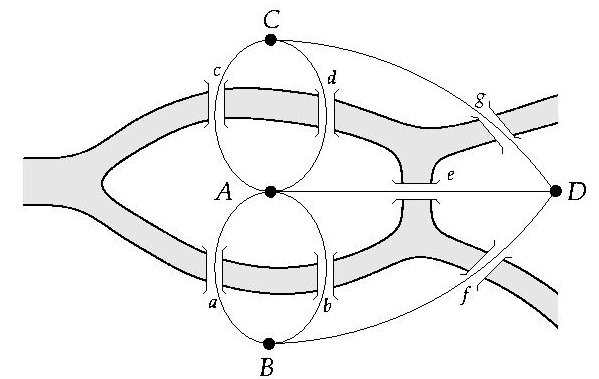
然后,假定你在图上沿着某条连边往前走。当你走到任意一个节点(图3里的A、B、C、D)时,如果它不是终点,那么你得走过它然后继续往前走。于是,这个节点有了两条连边:一条进、一条出。你就这样继续往前走。
你有可能再也不回到这个节点, 但也可能还会走回到这个节点来。因为它不是终点,如果走回来的话你还得离开它。这样它就有四条连边了。如此类推,它必须有偶数条连边。这里,重复走过某些节点是允许的,只是不允许重复走过任何一条连边。
最后,假定你走到了终点。原问题不是要求你走回到起点么?所以终点与起点重合,这个特殊的节点也同样有两条连边。
至此,问题是否有解的答案就很清楚了:如果有解的话,图中的所有节点都必须有偶数条连边。但是,图3所示的七桥数学图显然不满足这个条件,因此没有解:即不管你从哪里出发,你都不可能把七条桥全部走一遍,不重复也不遗漏,最后回到出发点。
欧拉后来以拉丁文正式发表了论文“关于位置几何问题的解法”(Solutio problematis ad geometriam situs pertinentis, Commentarii academiae scientiarum Petropolitanae, vol. 8, pp. 128-140, 1741),文中详细讨论了七桥问题并作了一些推广。该论文被认为是数学图论、拓扑学和网络科学的发端。

后来,欧拉和一些数学家分别考虑了一般多条桥的各种图,大家把其中有解的那些图称为欧拉图。具体地说,一幅规模有限的图,不管它有多少个节点和多少条连边,也不管你从哪个节点起步,如果总存在一条路径让你走遍所有的连边,不重复也不遗漏,最后还能回到起点,那么这幅图就是欧拉图。
从欧拉解决七桥问题开始,数学家们逐步建立起了数学图论,并把欧拉称为“图论之父”。
1771年,法国数学家范德蒙(Alexandre-Theophile Vandermonde,1735-1796)研究了国际象棋的“骑士”能否走遍棋盘每一个方格的游戏问题(Knight's Tour Problem)。
过了好多年之后,基于对上面两个图论游戏的兴趣,爱尔兰数学家哈密顿(Sir William R. Hamilton,1805-1865)考虑了一类和欧拉图“对偶”的图,就是不管一幅规模有限的图有多少个节点和多少条连边,也不管你从哪个节点起步,如果总存在一条路径让你走遍所有的节点,不重复也不遗漏,最后还能回到起点,这类图就称为哈密顿图。
哈密顿图对你走过多少条边,有没有遗漏一些边,都是没有限制的。因此,走遍一幅哈密顿图里所有节点的路径可能不是唯一的,因为也许会存在不同的路径都可以把所有的节点连在一起并且首尾相接。
![图5 [左] 欧拉(1707-1783);[右] 哈密顿(1805-1865)<br>](https://i.aiapi.me/h/2021/12/19/Dec_19_2021_03_36_19_26887149903298211.png)
二、哥尼斯堡名人录
自从欧拉解决了民间喜闻乐道的七桥问题之后,哥尼斯堡便走进了大众的视野。
其实,哥尼斯堡虽然历史不长,地域不大,但地灵人杰,名人很多。在哥尼斯堡出生长大的众多人物之中,我们只简单地说说“一、二、三”,即一位哲学家(康德)、二位物理学家(基尔霍夫和索末菲)和三位数学家(哥德巴赫、希尔伯特和闵可夫斯基)。
实际上,要比较完整地介绍他们之中任何一位的生平和贡献,都得写一本小书。此外,还有一些著名人物就不列举了,如化学家瓦拉赫(Otto Wallach,1847-1931)是 1910 年诺贝尔化学奖得主、数学家莫泽(Jurgen K. Moser,1928-1999)是数学动力系统KAM理论中的M、数学家黑塞(Ludwig O. Hesse,1811-1874)以他命名的矩阵(Hessian Matrix)为大家所熟识 ,还不计及文学、历史、政治、宗教、音乐、艺术等领域的名家。
1. 康德
哥尼斯堡最著名的市民当数哲学家康德(Immanuel Kant,1724年4月22日-1804年2月12日)。
康德是17-18世纪欧洲文艺复兴之后的反封建思想解放启蒙运动后期一位主要哲学家。他调和了笛卡儿的理性主义与培根的经验主义,发展了自成一派的思想体系,被认为是继苏格拉底、柏拉图和亚里斯多德后西方最具影响力的思想家之一。
康德有不少论著,其中核心的三大著作被合称为“三大批判”,即《纯粹理性批判》《实践理性批判》和《判断力批判》。这三部著作分别系统地阐述了他的知识学、伦理学和美学思想。《纯粹理性批判》一书被认为是西方哲学史上划时代的巨著。
此外,他在宗教哲学、法律哲学和历史哲学等方面都有重要贡献。一般认为,康德的道德哲学与中国儒家思想类似,强调个人道德自律从而构建理想社会。康德的道德原则就是“为道德而道德,为义务而义务”,包括“不要骗人”“不要自杀”“发展自己的才能”和“帮助别人”等方面,以致哲学家尼采(Friedrich W. Nietzsche,1844-1900)称康德为“哥尼斯堡的中国人”。
康德固然是一名哲学家,但也写过好几篇自然科学论文。1746年康德的父亲逝世,之后他开始了长达九年的家庭教师生涯。期间,他发表了两篇科学论文:1754年的“地球在绕轴自转时是否发生变化”和1755年的“从物理学上推论地球是否已经衰老”。
1755年,康德写了一篇学术论文“论火”,以此获得硕士学位。在同一年,他又写了“形而上学认识第一原理的新说明”一文,从而获得皇家哥尼斯堡大学(Royal Albertus University of Königsberg)任教的机会,在那里担任了15年的编外讲师。
康德性格内向,毕生都没有离开过家乡哥尼斯堡。他长期身体虚弱,过着极简生活,终身未娶。康德逝世后,墓碑上刻着他那本名著《实践理性批判》里的一句话︰“群星苍穹在我之上,道德法则存我心中”(Der bestirnte Himmel über mir und das moralische Gesetz in mir),作为他一生的总结。
2. 基尔霍夫
基尔霍夫(Gustav R. Kirchhoff,1824年3月12日-1887年10月17日)在1847年从哥尼斯堡大学物理系毕业。在大学期间,基尔霍夫一直参加数学物理学家诺依曼(Franz E. Neumann,1789-1895)和雅可比(Carl G. J. Jacobi,1804-1851)领导的研究讨论班,深受数学熏陶。
这位雅可比以他的矩阵和行列式为理工科师生所熟识。他出生于当年属于普鲁士的波茨坦,1826年到哥尼斯堡大学任教,在那里工作了16年,之后因健康问题退隐柏林。
1845年,还是本科生的21岁基尔霍夫发表第一篇论文,就建立了电路网络中电流、电压、电阻关系的两条基本定律,即以他命名的“电流定律”和“电压定律”,成为分析、计算和设计各种复杂电路不可或缺的基础理论和工具。
他后来又研究了电路中电的流动和分布,阐明了电路中两点间的电势和静电学的电势这两个物理量在量纲和单位上是一致的,从而使基本电路定律具有更一般的涵义和应用。基尔霍夫因此在电子和电器工程领域极负盛名,被称为“电路求解大师”。
1850年,基尔霍夫在柏林大学执教时发表了论文“弹性圆板的平衡与运动”,从三维弹性力学的变分开始,引进了著名的“基尔霍夫薄板假设”并给出了边界条件,还导出了圆板的自由振动解和一般振动表达式。
1854年,基尔霍夫由著名化学家本生(Robert W. Bunsen,1811-1899)推荐,到了海德堡大学任职教授。
1859年,基尔霍夫与本生合作,制成第一台光谱仪并创立了光谱化学分析法,由此发现了元素銫和銣。随后,其他科学家利用光谱化学分析法,还发现了鉈和碘等几种新元素。基尔霍夫进而利用光谱化学分析法去研究了太阳及一些行星的化学元素谱。
1860年,基尔霍夫做了灯焰烧灼食盐的实验,得出了“热辐射基尔霍夫定律”:任何物体电磁辐射的发射量和吸收量的比值与物体本身特性无关,是波长和温度的普适函数,与吸收系数成正比。他由此判断:太阳光谱的暗线是白光被大气中某些元素吸收的结果。这给太阳和恆星成分的分析提供了一种有效的方法,让天体物理进入了光谱分析的新阶段。接着,他又提出了绝对黑体的新概念。
1862年,基尔霍夫因在太阳光和人造光光谱研究中的重要贡献而荣获Rumford奖章。
1875年,基尔霍夫回到了柏林大学任职理论物理教授。其时,他给出了惠更斯-菲涅耳(Huygens–Fresnel)原理的严格数学形式,并发表了4卷《数学物理学讲义》。
1887年10月17日,基尔霍夫病逝于柏林,享年63岁。

3. 索末菲
索末菲(Arnold J. W. Sommerfeld,1868年12月5日-1951年4月26日)1886年进入哥尼斯堡大学主修数学,1891 年23岁时获博士学位。他随后出任哥廷根大学助教 。1897年,他转到Clausthal矿业学校任教授,1900年再转到Aachen技术学院任教授,1906年起到慕尼黑大学任理论物理学教授直至退休。1951年4月26日在慕尼黑意外被汽车撞倒不治离世,时年83岁。
索末菲的主要科学建树在原子结构及原子光谱理论方面。他提出用椭圆轨道代替玻尔(Niels H. D. Bohr,1885-1962)原子模型的圆形轨道,从而建立了“玻尔-索末菲原子模型”。
他还引入原子轨道空间量子化等概念,成功地解释了氢原子光谱和重元素 X 射线谱的精细结构以及正常Zeeman效应。此外,他对陀螺运动、电磁波传播以及金属电子理论多有贡献。
索末菲是一位出色的导师,先后带出了七个诺贝尔奖得主,包括德拜(Peter Debye, 1884-1966)、泡利(Wolfgang Pauli,1900-1958)、海森堡(Werner K. Heisenberg,1901-1976)、贝特(Hans Bethe,1906-2005)等四位博士学生和鲍林(Linus Pauling,1901-1994)、拉比(Isidor I. Rabi,1898-1988)、劳厄(Max von Laue,1879-1960)等三位博士后,还有一批卓有建树的博士生、博士后和合作者,以及几个后来获诺贝尔奖的学术梯队成员。
爱因斯坦曾感叹地对索末菲说:“我特别钦佩你的是,你能够从平凡中制造出那么多的年轻天才。”
索末菲一生得过许多的奖励和荣誉,是多个国家的科学院院士,并得到过世界上多所大学颁发的荣誉博士学位。
值得一提的是,索末菲明确坚定地反对纳粹的反犹太运动和所谓的“德意志物理学”,因而被攻击为“学术界中犹太文化的代理人”。但他毫无畏惧,从未退让过。
4. 哥德巴赫
哥德巴赫(Christian Goldbach,1690年3月18日-1764年11月20日)于1710年从哥尼斯堡大学毕业后游学欧洲至1724年,到过德国多个地方以及英格兰、荷兰、意大利和法国。特别是,他拜访过莱布尼兹(Gottfried W. Leibniz,1646-1716)、欧拉和贝努里(Nicholas I. Bernoulli,1687-1759)等大数学家。
1724年他回到哥尼斯堡之后,又与数学家比尔芬格(Georg B. Bilfinger,1693-1750)和赫尔曼(Jakob Hermann,1678-1733)结为好友,多有合作。
1725年,哥德巴赫到了圣彼得堡科学院任职数学和科学史教授,1728年成为俄罗斯沙皇二世的宫庭教师,1742年后还曾任职俄罗斯外交部。
哥德巴赫在数学分析方面有出色的贡献,例如有一条哥德巴赫-欧拉定理。但他主要贡献在数论方面,例如关于费马数(Fermat numbers)有一条哥德巴赫定理。
当然,他最出名的是在1742年6月7日写给欧拉信中提出的“哥德巴赫猜想”:任何一个大于2的偶数都可写成两个质数之和,俗称为“1+1”问题。当今最好的结果是陈景润1966年证明的“1+2”,但尚不是问题的终结。

5. 希尔伯特
希尔伯特(David Hilbert,1862年1月23日-1943年2月14日)被称为“数学界的无冕之王”、“数学中的帅才”,是历史上最卓越的数学家之一。
希尔伯特1880年进入哥尼斯堡大学,但他执意违背父亲让他学习法律的意愿,选择了数学,于1885年23岁时获得博士学位,之后留校任讲师、副教授,1893年升为正教授。
1895年,希尔伯特接受克莱因(Christian F. Klein,1849-1925)邀请到了哥廷根(Göttingen)大学任教,直至1930年退休,于1943年逝世,享年81岁。
希尔伯特曾获俄罗斯罗巴切夫斯基奖和瑞典科学院Mittag-Leffler奖,1942年当选为柏林科学院荣誉院士。
希尔伯特在不变量理论、代数数论、积分方程、变分法、泛函分析、数学和几何学基础、数学物理等领域中作出了十分重要的贡献。其中最值得提及的是他1900年8月8日在巴黎第二届国际数学家大会上的著名演讲。他指出了新世纪数学家应当努力解决的23个数学问题,其中第8个问题包含了哥德巴赫猜想。
那次演讲被认为是20世纪数学最重要问题的选集。对那些问题的研究,后来大大推动了数学的进步并对今天数学的发展依然有着深刻影响。1950年,当美国数学会邀请希尔伯特的博士学生、著名数学家外尔(Hermann K. H. Weyl,1885-1955)总结20世纪上半页的数学历史时,外尔写道:
希尔伯特在巴黎提出的23个数学问题“是一张导航图”;在过去五十年间,“数学家们经常按照这张导航图去衡量我们的进步”。
希尔伯特同时也十分关注物理学,曾把他认为“数学较差”的爱因斯坦请到哥廷根大学,一起讨论后来被称为“爱因斯坦方程”的物理学含义。期间,数理逻辑学家哥德尔(Kurt F.Gödel,1906-1978)为爱因斯坦方程找到一个解,让他满载而归。
希尔伯特去世后,在哥廷根的墓上刻着他退休感言中的最后一句话:“我们必须知道,我们必将知道”(Wir müssen wissen,Wir werden wissen)。

6. 闵可夫斯基
闵可夫斯基(Hermann Minkowski,1864年6月22日-1909年1月12日)为理工科的学者们所熟识,很可能是由于数学分析中的“闵可夫斯基不等式”。
闵可夫斯基1864年出生于俄国的Alexotas(今立陶宛的Kaunas)。由于当时俄国政府迫害犹太人,1872年父亲带着全家移居到了哥尼斯堡。他们家与希尔伯特的家仅一河之隔,两人从小相识。
1879年闵可夫斯基入读于柏林大学,不久转回哥尼斯堡大学。大学期间,他授课于亥姆霍兹(Hermann L. F. von Helmholtz,1821-1894)、克罗内克(Leopold Kronecker, 1823-1891)、维尔斯特拉斯(Karl T. W. Weierstrass,1815-1897)、基尔霍夫等物理学家和数学家。
1882年,年仅18岁的闵可夫斯基因为建立了多元二次型的完整理论与英国著名数学家史密斯(Henry J. S. Smith,1826-1883)共同分享了法国科学院的一个大奖,名噪一时。1885年,21岁的闵可夫斯基在哥尼斯堡大学获得博士学位。
1886年,他成为波恩大学讲师,然后于1891年升为副教授。1894年,他回到哥尼斯堡大学任教。1895年,希尔伯特离开哥尼斯堡前往哥廷根大学,由闵可夫斯基接替他的位置担任数学教授。次年,闵可夫斯基又转到瑞士苏黎世联邦理工学院(ETH Zürich)任教。
期间,青年爱因斯坦在该校就读,成为闵可夫斯基的学生。1902年,闵可夫斯基接受克莱因的邀请,加盟哥廷根大学担任数学教授直至离世。
闵可夫斯基最具独创性的成果是他在1890年开创的“数的几何”(Geometrie der Zahlen),书稿在1896年基本完成,于1910年正式出版。他关于数的几何理论的研究导致了对凸体填充问题的研究,即给定形状的图形可以放置到另一个给定形状图形中的个数和方法,其中引出了大家熟知的“閔可夫斯基不等式”。
1905年,闵可夫斯基建立了实系数正定二次型的“闵可夫斯基约化理论”。1908年,在Cologne的一次著名学术演讲中,闵可夫斯基提出了四维时空的概念,为后来爱因斯坦的广义相对论提供了基本框架,被称为“闵可夫斯基时空”理论。
1909年1月11日,闵可夫斯基因急性阑尾炎抢救无效在哥廷根逝世,时年仅45岁。希尔伯特随即整理了他的遗作,于1911年出版了《闵可夫斯基全集》(Gesammelte Abhandlungen von Hermann Minkowski)。

三、加里宁格勒
现在,让我们回到哥尼斯堡。
然而,今天普鲁士不复存在,哥尼斯堡也不复存在。
第二次世界大战末,哥尼斯堡被轰炸得天翻地覆。1945年4月9日,苏联军队完全占领了哥尼斯堡。同年8月2日,苏、美、英三国在柏林联合发表了《波茨坦公告》。根据公告的决议,战败的德国将东普鲁士地区割让给波兰和苏联。
其中,行政上哥尼斯堡成了苏联领地。但地理上,城堡与苏联本土不但互不邻接,而且相去甚远,中间隔着立陶宛和白俄罗斯,因此被戏称为“飞地”。
1946年,苏联政府把哥尼斯堡改名为加里宁格勒(Kaliningrad),以纪念刚去世的最高苏维埃主席团主席加里宁(Mikhail I. Kalinin,1875-1946)。两年之后,苏联政府又把哥尼斯堡大学改名为“加里宁格勒国立师范学院”,1967年再更名为“加里宁格勒国立大学”。
哥尼斯堡也罢,加里宁格勒也罢,现在让我们回到“哥尼斯堡七桥问题”。
早在1875年,由于民生的需要哥尼斯堡市政府在图3中的B点和C点之间修建了一道桥。但是,这“八桥问题”依然没有解,即不存在一条路径让你把8道桥不重复也不遗漏地走一遍,最后回到出发点。
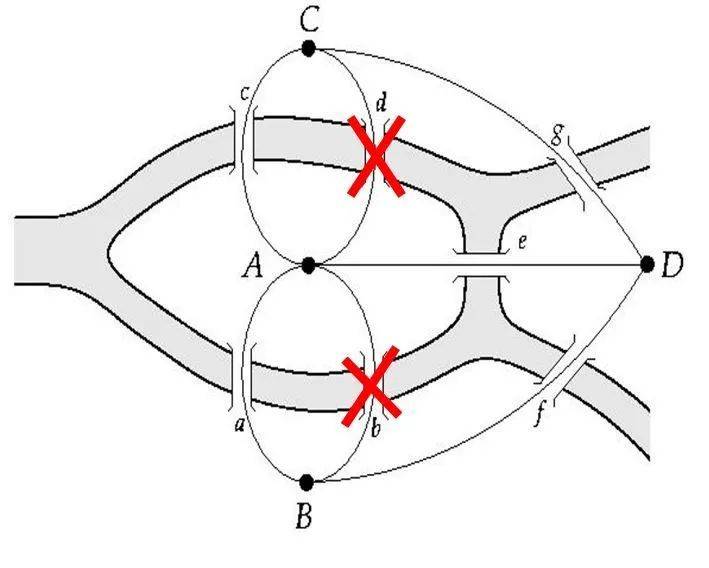
1944年,哥尼斯堡的七条老桥在战火中被全部炸毁。后来,加里宁市政府修复了五道桥(图3中的A-B和A-C之间分别只修复了一道桥),保存至今。现在这些老桥主要供旅游观光使用。

最后,如果你明白前面欧拉关于七桥问题无解的解释的话,你就会知道这“加里宁格勒五桥问题”(图14)也是没有解的。
本文来自微信公众号:集智俱乐部(ID:swarma_org),作者:陈关荣

