近年来在量子引力方面最重要的进展之一,就是关于黑洞信息悖论(或称佯谬)的问题得到了回答:几位年轻学者,通过引入量子极值面找到了佩奇曲线的转折点,量子黑洞蒸发过程不会丢失信息。去年《返朴》曾简要介绍过这项工作《黑洞信息悖论之谜,霍金最后的问题被解决了吗?》,现在,我们来听听论文作者Netta Engelhard的说法,她是如何破解黑洞信息悖论的。
本文来自微信公众号:返朴(ID:fanpu2019),采访者:Natalie Wolchover,受访人:Netta Engelhard,编译:董唯元,头图来自:视觉中国
延续了半个世纪的黑洞信息悖论,一直被认为是通往量子引力理论的关键路标之一。在新一代迎难而上的研究者中,Netta Engelhardt俨然已成为佼佼者。
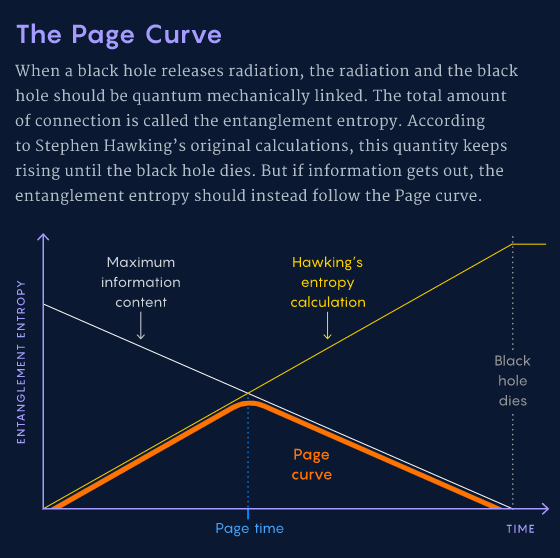
所以问题就变成了究竟哪条熵值变化曲线是正确的。一般来说,熵是指系统里宏观无法区分的微观可能构型的总数。在黑洞的语境下应该怎么理解熵的含义?
你可以理解成对黑洞内部事件状态的无知程度。想想黑洞内部可能会发生什么,各种可能性越多,你的无知程度就越大,对系统究竟处于哪种构型就越无知。所以熵就是度量无知的程度。
Page的发现是说,如果你认定宇宙的演化不会造成信息丢失,那么当黑洞形成之前你的无知程度为零,最终黑洞消亡之后你的无知程度仍应该回到零,所有进入黑洞的信息都该被释放出来。与之相矛盾的是霍金的推导,他的结论是最终的无知程度增加了。
您把Page的研究以及2019年之前的其他研究成果都归结为“对问题更好的理解”,2019年这一年发生了什么?
2019年的进展才是真正开始解决问题。有两篇论文迈出了这一步,其中一篇是我与Ahmed Almheiri、Don Marolf 和 Henry Maxfield的研究。另一篇论文来自Geoff Penington。经过协商,我们在同一天提交了论文,因为我们都知道大家同时触及到了相同的东西。
主要思想就是用不同的方法重新计算熵值,这也是为什么Don Page的见解对我们很重要。如果我们采用霍金的方法及假设条件,得到的熵值计算公式与幺正性肯定无法相容。我们需要搞明白的是,是否可以找到合理的计算方法能满足Page的理论,就是那根先升后降的曲线。
对此,我们依靠了Aron Wall和我在2014年提出的量子极值面,那是一个经过量子化校正的黑洞内的曲面,其面积与熵值的计算有关。当时我们觉得那应该是处理量子引力相关计算的可行途径,也许能给出满足幺正性的结果。现在看起来,我得说那个出发点其实带有撞大运的成分。
那您什么时候开始意识到这条途径真的可行呢?
那段时间的记忆其实已经有些模糊了,因为实在太兴奋了。所有的计算结果汇总大概历经了三周时间,印象中那几周里我每天可能就睡两个小时。那时候我还在普林斯顿,我们就在校园的草地上开会。我有个特别的记忆,在开车回家的路上,我的脑海里一直在想,哇哦,应该就是它了。
关键的症结在于,其实有不止一个量子极值面存在。其中一个量子极值面给出错误的结果,就是霍金的结论。想正确的计算熵值,必须得先选择正确的量子极值面,而正确的意思,就是具有最小的量子修正面积。而真正激动的时刻,就是我们意识到这种方法真的可能成功时——熵曲线需要反转(从增大到减小),而我们恰好发现了这个反转的点。
原来熵曲线的反转时刻,就对应着正确的量子极值面发生了跳跃。起初阶段,正确的量子极值面就是霍金的计算所对应的那个,在某个时间点,正确的量子极值面会跳转到另一个新的曲面,而这个新的量子极值面会给出反转之后的Page曲线。
那些量子极值面到底是什么?
我试试描述一个经典的、非量子的极值面在直觉上是什么样子。让我们从一个球面开始,想象球里有一个灯泡,你跟着光线的传播一起运动并穿过球面。显然光线传播的越远,所穿过的球面面积就越大。我们就说,光线的横截面积在变大。
这很符合我们在平直空间中所体会到的直觉,可是在黑洞这种时空强烈弯曲的地方,景象会十分古怪。尽管光线仍然是从灯泡朝外射出,跟随光线运动的你却会看到球面在渐渐远离而不是靠近,光线横截面积实际是在缩小。这种由强烈的时空弯曲导致的现象,我们称为光线汇聚(译注:测地线汇聚),是广义相对论里非常基础的概念。
极值面就恰好处在两种情况之间,横截面积既不会增加也不会缩小。直觉上说,你可以把极值面看做一种临界状态,那里曲率的强度恰好还未达到过分的程度。量子极值面的意思也没什么差别,只是不再使用普通的面积计算,而是要看量子修正面积。总之极值面处的面积总是不变,于是此处的熵值也就既不增加也不减少。(译注:纠缠熵与量子极值面面积呈正比。)
量子极值面有什么意义?处在极值面内部和外部又有什么区别?
如刚才所说,当Page曲线发生反转,我们对黑洞内部的无知程度应该开始下降,而接触到的黑洞辐射越来越多,也就是我们应该能够从黑洞辐射中获取信息。所以这些来自黑洞的辐射,必须开始掌握并携带黑洞内部的信息。
量子极值面把时空一分为二:在极值面内部,信息已经被辐射顺利掌握;而在极值面以外,一切都还是黑洞保守的秘密,辐射无法获取这部分信息。随着黑洞产生更多的辐射,量子极值面也向外移动,包含的体积也就越来越大。最终在黑洞彻底蒸发殆尽时,黑洞中的所有秘密,都可以被辐射探知并携带出去。
现在我们明确地计算出了满足幺正性的答案,这给了我们许多工具,可以开始问一些以前无法提出的问题。比如数学形式为什么会是这个样子,它又与哪种类型的量子引力理论存在联系?还有,量子引力理论中的什么机制使幺正性得以恢复?这些都与量子极值面的公式有关。
量子极值面的公式和结论几乎都是在带有边界的“反德西特(AdS,Anti-de Sitter)”空间中研究得到的,那是负曲率的空间。而我们的宇宙基本上是平坦的,也没有边界。为什么认为那些计算结果也能适用于我们的宇宙?
首先,无法回避的事实是,我们的宇宙中既存在量子机制也存在引力,还有黑洞。如果不明白黑洞内部发生了什么,对宇宙的理解就始终流于片面。信息悖论问题既艰难又关键,即使是在简化模型上取得的进展,也是在推动和提升对我们这个宇宙的理解。
在更技术的层面,量子极值面可以用来计算各种不同的时空,包括我们宇宙的平坦时空。实际上已经有论文在讨论其他类型时空中的量子极值面和相应的熵曲线。
我们对AdS空间中的量子极值面已经有了非常牢靠的认知,推广到平坦空间中,也有类似意义下的量子极值面,我想这一点应该没什么问题。它有许多很好的性质,也应该是个正确的方向。我们能看到它表现出非常有趣的行为,我们也期望幺正性能够得以展现。当然许多行为和现象还需要进一步解读,研究起来也不容易。
在对话刚开始的时候您曾说,我们尚未得到信息悖论的答案,能否描述一下完整的答案应该是什么样?
完整的答案应该告诉我们信息究竟是如何从黑洞里逃出来的。如果我是一个待在黑洞外面的全能观测者,拥有极致的技术手段和足够长的时间,比如我有一台能够完全测量黑洞所有辐射的量子计算机。在这种情况下,我该如何根据辐射来解码其中的信息,并根据这些信息重现历史?比如还原出塌缩成黑洞的那个星体前身,我该为此给我的量子计算机编写什么样的程序算法?这些都是我们需要回答的问题。
听起来您是希望找到在辐射中还原出信息的解码算法,这跟量子引力有关联吗?
研究从霍金辐射中解码信息的算法,就是研究在黑洞视界附近量子引力如何把信息编码进辐射中的过程。黑洞内部的形成,黑洞内部的动力学行为,一个物体落入黑洞之后所经历的过程,所有这些黑洞视界背后的历史,都被量子引力编码进了辐射(译注:辐射产生于黑洞外临近视界处)。那么必然要问的问题就是,信息究竟是如何被编码进霍金辐射中的?
您最近在写的论文题目叫“蟒蛇的午餐”(python’s lunch),那是什么?
是关于如何解码霍金辐射的。你也许还想问这项工作的复杂性,事实证明,那真是出人意料的超级复杂。也许霍金当初的计算之所以丢失了幺正性,而量子极值面的计算可以保留幺正性,就是因为霍金放弃了这些复杂性过高的操作。
我们可以从几何视角来理解一下这些复杂性。2019年我的几位同事写了篇论文,他们指出,一旦存在超过一张量子极值面,麻烦就出现了。首先是传统用熵来衡量解码复杂度的对应关系就失灵了。其次,量子极值面可看做一种时空几何的限制条件,借用《小王子》中的场景来说,我们会看到蟒蛇的肚子里有一头大象。于是就有了“蟒蛇的午餐”的说法。
我们觉得,多量子极值面的存在,是带来超级复杂度的根本原因。你所提到的那两篇论文,主要就是论证“强蟒蛇午餐”观点。这些工作能帮助我们加深洞察,厘清了哪部分几何是霍金计算中已经体现的,哪部分是遗漏的。将霍金计算所使用的数学语言和我们使用量子极值面计算时所使用的数学语言,放在同种数学语言中,更容易看清为什么其中一个结论是正确的,另一个不正确的具体错在哪里。
您如何评价我们在通往量子引力的路上当下所处的位置?
我觉得就像拼图游戏,我们拿着所有的边块,但是缺少中间的部分。我们对量子引力有许多不同角度的感知,也有许多可以深入探索的路径。有些从边界限制条件入手,说它不能是什么样子;有些从构造角度入手,研究它必须具备什么。我个人倾向就是从信息悖论着手,因为这是核心关键问题,而且非常尖锐直接,它能够清晰地告诉我们在哪里犯了错。在我看来,这项工作是在修葺理论基柱,未来支撑量子引力理论的基柱。现在这些基柱一定存在错漏有待修正。
本文来自微信公众号:返朴(ID:fanpu2019),采访者:Natalie Wolchover,受访人:Netta Engelhard,编译:董唯元

