本文来自微信公众号：集智俱乐部（ID：swarma_org），作者：Vijay Balasubramanian，翻译：张澳，审校：梁金，编辑：邓一雪，原标题为：《大脑为何如此耗能？比较计算与通信的代谢能效》，题图来自：视觉中国


一、大脑能量消耗之谜


人脑仅占体重的 2%，却占人体代谢负荷的 20% [1-3]，单位质量的代谢成本是肌肉的10倍。另一方面，大脑能在大约 20瓦的能量预算下创作诗歌、艺术以及设计航天器——考虑到用来写作这篇文章的计算机就需要 80瓦的能耗，大脑的能耗简直微不足道。


大脑中何处消耗能量，能量被用来做什么？为什么大脑的代谢成本相对于其它生命活动如此高昂？大脑又是如何实现远高于硅基产品的能量效率？


许多经典论文都研究过这些问题。Attwell 和 Laughlin [4] 进行了详细的生物物理估计，表明神经信号传导和神经递质释放的突触后效应合起来占大脑三磷酸腺苷（ATP，生物体最直接的能量来源）消耗的 80%，这一结论也得到了神经生理学和解剖学的支持 [5, 6]。


许多研究探讨了这种能量消耗的结构及功能后果，包括限制大脑尺寸和缩放规律（size and scaling）、有效连线模式、模拟（分级电位）与数字（尖峰）信号、分布式神经代码、沿神经束的信息流量分布及其规模分布，还有计算异质性和效率等[8-17]。Sterling 和 Laughlin [18] 对这些想法进行综合，得出一系列大脑的设计原则。Levy 和 Calvert [19] 提出了哺乳动物大脑功率预算的功能解释，表明通信的代谢成本比计算高得多，并探索了神经回路组织的功能后果。


二、大脑中的通信和计算


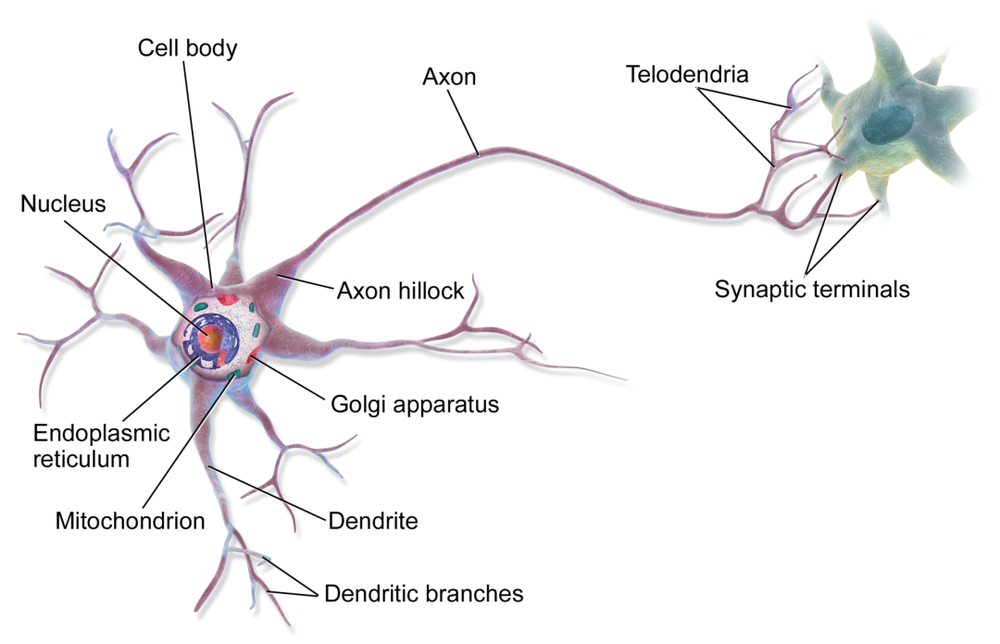
Levy 和 Calvert [19] 以早期文献为基础，主要关注人脑中不同信息处理模式的相对能耗，而不是细胞层面不同功能的能耗。它们对通信和计算做出了关键的区分：“通信”一般是指信息点到点的传输（可能以某种方式编码），不包括表征转换、特征提取或决策的映射。大脑中通信的一个例子是视觉信息沿视神经从眼睛到中央大脑的传输，这个过程中视觉信息保持不变。“计算”是一个更微妙的概念，通常从输入-输出转换的角度来理解。


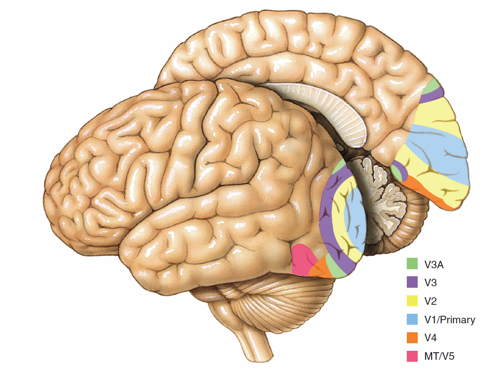
Levy 和 Calvert 在先前工作的基础上，将每个神经元视为对自身输入中的潜在变量进行“微观估计或预测”，并在脉冲间隔内（神经元两次传输信号的动作电位之间）对输出进行编码。微观估计和预测是极其一般化的框架，能够包含神经计算的其他观点（如将神经元视为动力系统或逻辑门），并且还包含了单个神经元在神经网络中的计算功能。同样，脉冲间隔中信息编码的形式也包含多种可能性，如速率编码和模式编码。因此，大脑中神经元“计算”的一个例子可以是 V1 区（见图1） 中的一个细胞对视神经输入信号的估计或预测，并将其编码为视觉上某个物体（如一条水平线）的存在。


图1.初级视觉皮层（V1），位于大脑内侧枕叶的距状沟中（后脑勺左右侧）。V1是皮层中的“第一个”视觉处理区域， LGN（外侧膝状体核，位于丘脑，接受视网膜大部分视觉信息输入）将大部分轴突信号发送至V1皮层。<br label=图片备注 class=text-img-note>
图1.初级视觉皮层（V1），位于大脑内侧枕叶的距状沟中（后脑勺左右侧）。V1是皮层中的“第一个”视觉处理区域， LGN（外侧膝状体核，位于丘脑，接受视网膜大部分视觉信息输入）将大部分轴突信号发送至V1皮层。


从这个角度出发，作者对比了计算中涉及的单位脉冲间隔的兴奋性电流中恢复离子梯度的 ATP 成本，以及通信中涉及的诸如轴突静息电位、动作电位和囊泡回收等成本，最终得出结论：通信相关的生物物理过程消耗的能量是计算相关过程的 35 倍（生物相关单位以每秒消耗 ATP 分子计，物理单位以每秒消耗焦耳计） [19]。


通信与计算能耗的巨大差异为参考文献 [4] 中隐含的发现正名，其作者表明神经信号传导和神经递质释放的突触后效应支配着大脑的功耗。来自参考文献 [15] 的另一条证据表明，神经元中的线粒体分布会追踪放电率和突触传递，因此轴突的粗细很可能取决于突触终端的能耗需求，它占哺乳动物大脑能耗的 65% [20]。


在先前建立的框架中，文献[4]与[15]中描述的高能耗过程都是通信过程，不包括文献[19]中的计算过程。有趣的是，Levy 和 Calvert 还估计，27% 的皮层能量支出是用于与突触发生相关的过程，例如通过肌动蛋白聚合、膜合成和掺入，以及相关的细胞内运输的生长。这进一步细化了先前的能量预算，表明大脑将四分之一以上的能量用于促进持续学习，这与我们对大脑的印象相一致。


图2.一个典型的神经元由胞体（cell body），树突（dendrite）和轴突（axon）组成，轴突的最远端是突触（synapse），神经元可以通过突触将信号传输到另一个细胞。<br label=图片备注 class=text-img-note>
图2.一个典型的神经元由胞体（cell body），树突（dendrite）和轴突（axon）组成，轴突的最远端是突触（synapse），神经元可以通过突触将信号传输到另一个细胞。


三、大脑耗能对计算机设计的启发


在物理层面，Levy 和 Calvert 计算出皮层灰质消耗了大约3瓦的功率，而根据大脑葡萄糖摄取量，估计大脑功率消耗为 17~20瓦[1 , 2]，其中 10% 在正常情况下未被使用，大约9瓦以热量形式耗散，剩余能量为大脑其余部分供能。


对皮层灰质 3瓦的功耗估计与 Lennie [21] 早期工作的结果一致。但 Lennie 使用 20 年前可用的数据，发现大脑能量预算的划分略有不同——大脑50%的功耗用于与神经电信号活动（即计算和通信）无关的过程。该结论与当前研究的差异部分来自于生物物理数据，包括对突触数量及其接通率（success rate）的估计。新的估计还表明，灰质中每个神经元的能耗大约为2×10-9瓦，这与 Herculano-Houzel的工作一致[22] 。


Levy 和 Calvert 根据噪声神经积分器输入和输出之间的互信息，来估计大脑每焦耳能耗所计算的信息比特数。在这个定义下，他们发现神经元每比特的计算能耗是 Landauer 理想热力学极限*[23] 的108倍。他们认为这一巨大差异源于通信成本（Landauer 忽略了这一点）和生物需要快速响应行为的计算需求。通信成本和快速计算需求这两个约束无疑是相关的，研究人员希望在未来仔细检验关于计算的定义，以及由活细胞计算施加的生物物理约束。


*译注：Landauer 原理表明，擦除1比特信息在理论上至少要产生kBTln2 的能量耗散，这被称为Landauer极限。


在 Levy 和 Calvert 的分析中，能量预算和每焦耳能耗所计算的比特数都取决于一个参数：皮质锥体神经元的平均输入突触数乘以它们的接通率。他们发现，当这个参数大约为 2000 时，每焦耳能耗所计算的比特数估值将最大化，接近于他们从数据中得出的值。这个有趣的结果让人想起之前使用能源效率来理解神经放电应该如何组织的研究 [11, 13]，以及信息应该如何在大脑中的细胞和结构之间进行分配的研究 [14, 17]。这项新工作为更精细地分析大脑中的回路结构以及大脑如何划分计算任务打开了大门。


图3. 大脑中的计算分布在网络中通信的特定组件之间。绿色圆圈表示皮质区域网络，每个区域执行不同的功能。橙色三角形表示锥体细胞网络，它们通过协作计算单个皮质区域的功能。Levy 和 Calvert 认为基本单元的计算成本相比于它们之间的通信成本而言微不足道。<br label=图片备注 class=text-img-note>
图3. 大脑中的计算分布在网络中通信的特定组件之间。绿色圆圈表示皮质区域网络，每个区域执行不同的功能。橙色三角形表示锥体细胞网络，它们通过协作计算单个皮质区域的功能。Levy 和 Calvert 认为基本单元的计算成本相比于它们之间的通信成本而言微不足道。


Levy 和 Calvert 的结果与在持续计算和通信方面解释区域脑代谢的功能性磁共振成像（fMRI）测量值是相关的。新数据也适用于对大脑演化的研究，如针对大脑代谢成本高昂 [7] 及代谢生理上限制大脑结构 [8, 22] 的研究。


Levy 的研究结果也会引发工程师对设计下一代低功耗智能计算设备的兴趣。研究指出由大脑灰质完成的计算和通信仅需3瓦的功率，即使加上用于保温的9瓦功率，这一功耗也比典型的笔记本电脑低出近一个数量级。


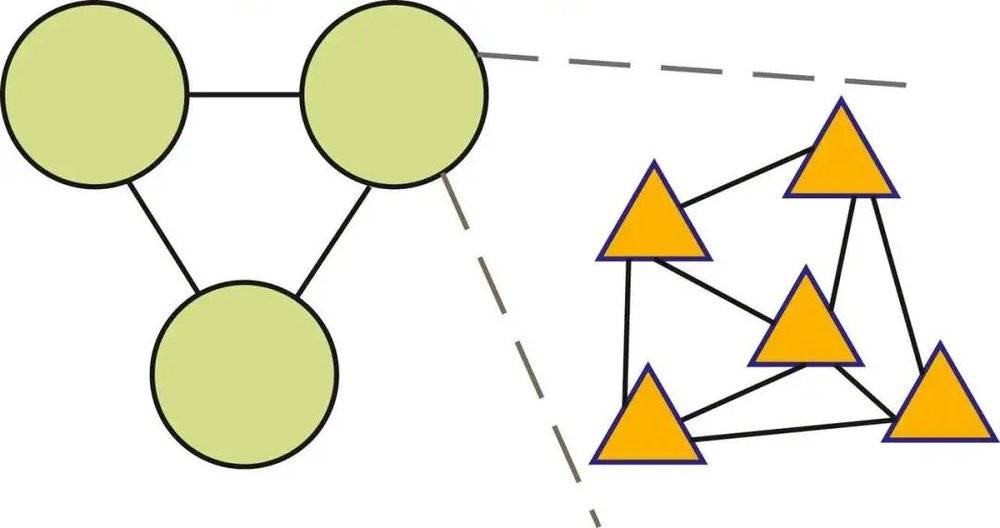
先前的工作表明，信息处理速率和能耗间存在的收益递减规律将推动计算机向异构架构发展，在这种架构中，整体功能在各尺度上通过大量特定单元间的协作涌现，每个特定单元以物理基质决定的最高效率处理信息[17]。Levy 和 Calvert 的论文表明，这种向异构架构的转变必须平衡好不同组件之间的网络学习成本和通信成本，因为尽管每个单元的计算成本相对较低，但单元间的通信成本将是高昂的。


参考文献：

[1] L. Sokoloff, “The metabolism of the central nervous system in vivo” in Neurophysiology, J. Field, H. W. Magoun, V. E. Hall, Eds. (Handbook of Physiology, American Physiological Society, 1960), sec. 1, vol. 3, pp. 1843–1864.

[2] B. K. Siesjö, Brain Energy Metabolism (John Wiley, 1978).

[3] D. F. Rolfe, G. C. Brown, Cellular energy utilization and molecular origin of standard metabolic rate in mammals. Physiol. Rev. 77, 731–758 (1997).

[4] D. Attwell, S. B. Laughlin, An energy budget for signaling in the grey matter of the brain. J. Cerebr. Blood Flow Metab. 21, 1133–1145 (2001).

[5] A. Ames 3rd, CNS energy metabolism as related to function. Brain Res. Brain Res. Rev. 34, 4 2–68 (2000).

[6] V. Braitenberg, A. Schüz, Anatomy of the Cortex: Statistics and Geometry (Springer Science & Business Media, 2013), vol. 18

[7] L. C. Aiello, P. Wheeler, The expensive-tissue hypothesis: The brain and the digestive system in human and primate evolution. Curr. Anthropol. 36, 199–221 (1995).

[8] K. Fonseca-Azevedo, S. Herculano-Houzel, Metabolic constraint imposes tradeoff between body size and number of brain neurons in human evolution. Proc. Natl. Acad. Sci. U.S.A. 109, 18571–18576 (2012).

[9] D. B. Chklovskii, A. A. Koulakov, Maps in the brain: What can we learn from them? Annu. Rev. Neurosci. 27, 3 6 9–392 (2004).

[10] R. Sarpeshkar, Analog versus digital: Extrapolating from electronics to neurobiology. Neural Comput. 10, 1601–1638 (1998).

[11] W. B. Levy, R. A. Baxter, Energy efficient neural codes. Neural Comput. 8, 531–543 (1996).

[12] B. T. Vincent, R. J. Baddeley, T. Troscianko, I. D. Gilchrist, Is the early visual system optimised to be energy efficient? Network 16, 1 7 5–190 (2005).

[13] V. Balasubramanian, D. Kimber, M. J. Berry, 2nd, Metabolically efficient information processing. Neural Comput. 13, 7 9 9–815 (2001).

[14] K. Koch et al., How much the eye tells the brain. Curr. Biol. 16, 1428–1434 (2006).

[15] J. A. Perge, J. E. Niven, E. Mugnaini, V. Balasubramanian, P. Sterling, Why do axons differ in caliber? J. Neurosci. 32, 626–638 (2012).

[16] V. Balasubramanian, P. Sterling, Receptive fields and functional architecture in the retina. J. Physiol. 587, 2753–2767 (2009).

[17] V. Balasubramanian, Heterogeneity and efficiency in the brain. Proc. IEEE 103, 1346–1358 (2015).

[18] P. Sterling, S. Laughlin, Principles of Neural Design (MIT Press, 2015).

[19] W. B. Levy, V. G. Calvert, Communication consumes 35 times more energy than computation in the human cortex, but both costs are needed to predict synapse number. Proc. Natl. Acad. Sci. U.S.A. 118, e2008173118 (2021).

[20] B. Sengupta, M. Stemmler, S. B. Laughlin, J. E. Niven, Action potential energy efficiency varies among neuron types in vertebrates and invertebrates. PLOS Comput. Biol. 6, e1000840 (2010).

[21] P. Lennie, The cost of cortical computation. Curr. Biol. 13, 49 3–497 (2003).

[22] S. Herculano-Houzel, Scaling of brain metabolism with a fixed energy budget per neuron: Implications for neuronal activity, plasticity and evolution. PLoS One 6, e17514 (2011).

[23] R. Landauer, Irreversibility and heat generation in the computing process. IBM J. Res. Dev. 5, 1 8 3–191 (1961).


原文：https://www.pnas.org/content/118/32/e2107022118


本文来自微信公众号：集智俱乐部（ID：swarma_org），作者：Vijay Balasubramanian