本文来自微信公众号:集智俱乐部(ID:swarma_org),作者:Moritz Helias,译者:郭瑞东,审校:赵雨亭,原文标题:《PRL:大脑动力学——在临界点左右徘徊》,题图来自:《超体》
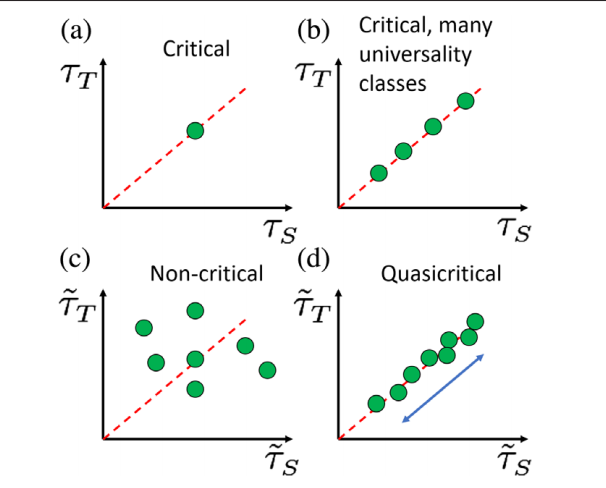
许多证据表明,生物大脑皮层普遍在临界点附近运行,但目前尚未发现普适的标度。事实上,不同物种之间、同一物种不同个体之间、同一个体不同时刻之间,动力学的标度会有很大差异。怎样理解其中的差异性和统一性?近日,一篇发表于《Physics Review Letters》的论文指出:外部输入迫使大脑的神经网络远离临界点,在非平衡状态下运行。不同的条件下,大脑都处于一类满足标度关系的“准临界态”。
 论文题目:Evidence for Quasicritical Brain Dynamics
论文题目:Evidence for Quasicritical Brain Dynamics
论文地址:https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.126.098101
临界态,描述多种现象的一般性模型
许多不同物理系统的动力学可以用一个单一的数学模型来描述。看似毫无共同点的系统(例如水从沙子中渗透,或者在岩石中裂缝的扩散)都处于临界态事件(critical phenomena)。
已有研究表明,大脑中的神经元网络代表了这一类事件中的另一个关键系统,而其他研究则揭示了神经元会呈现偏离临界状态的行为。现在,印地安那大学伯明顿分校的 Leandro Fosque 和他的同事们表明,大脑可能是“准临界的”:它被持续不断的外部刺激驱离临界点[1]。他们发现,这种转变并不是随机的,而是以一种大脑对刺激反应最大化的方式发生——这种反应模式是大脑处理信息的核心特征。
在大脑中,临界状态指的是神经元活动被刺激(如感觉输入)所触发的方式。这种活动以类似连续雪崩的方式传播——在 t 时间段内,s 神经元短暂地连续发射。T 和 s 随时间的变化服从幂律分布,呈现出无标度的临界态行为模式[2]。如下图所示:
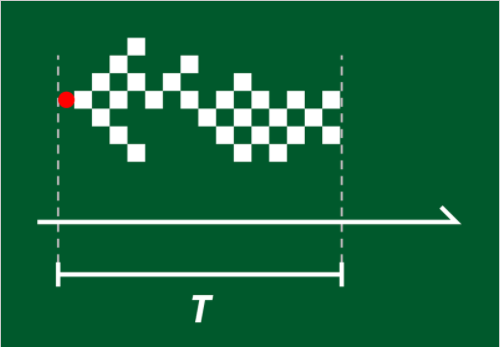
在体外培养的神经元网络中,相应的幂律指数 τt 和 τs (描述在特定的t和s时,雪崩如何随时间的分布)是常数,且是一个可以用“定向渗流”分支过程来模拟的通用类。在这个模型中,每个节点代表一个神经元放电,而分支代表从该神经元传递到一个或多个“后代”。当分支系数(每个活动神经元的子代数量)位于两个相变点附近时,网络呈临界状态:一方面,神经元间的级联连接能迅速被抑制;另一方面,神经元的级联连接以自我维持的的方式进行。
大脑中神经的动力学不符合临界态
实验室中,表现出上述临界状态的神经网络很小,且相对简单。但是活体大脑是复杂的,虽然 t 和 s 仍然呈幂律分布,但实验表明,τt 和 τs 在物种、实验条件、时间和刺激物下存在差异,这一发现从根本上与大脑的神经活动是普遍临界态的一个特例相矛盾[3]。
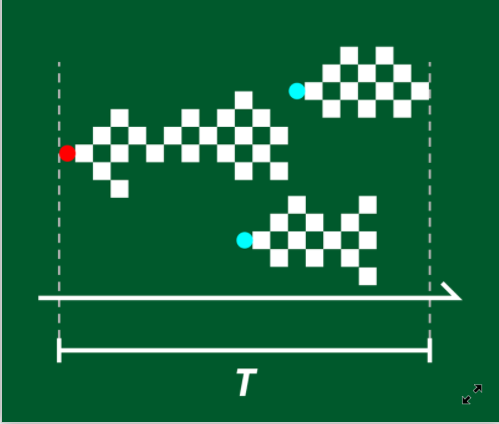
Fosque和他的同事通过结合模拟神经网络,和对啮齿动物神经元数据的分析来解释这些指数的变化。他们的临界分支模型考虑了定向渗滤的一个重要方面,即神经元激活的动力学。该模型在神经元培养皿与活体大脑之间是不同的:即吸收状态(由于随机性,当所有神经元在同一时刻处于未激活状态时,大脑活动的停止)存在不同。这种状态对于神经元雪崩式传播的结束至关重要:在一个小型的孤立网络中,吸收状态很容易达到,但在一个大型的、相互连接的网络中就很难实现。
大脑神经动力学无法保持临界态的原因
造成这种差异的原因是,人工培养的神经网络很小,神经元之间的相互作用必然是局部的。相比之下,活体大脑皮层的一部分,大约 50% 的输入信号来自其他较远的脑区。Fosque 和他同事们的模型解释了这些远程刺激,让每个神经元以概率 p 自发激活。在定向渗滤模型中,这意味着雪崩式传播不是由单个神经元引发的,而是可以在任何时间点自发发生。
这些间歇性活动增加了雪崩式传播的持续时间和规模,并导致 τt 和 τs 值变小,这意味着该系统不再属于临界态的一个特例。这种自发的雪崩活动也在时间上打破了严格的尺度不变性,因为它暗示了一个自发激活的时间尺度符合 1/ps 的幂律分布。该特征指出,从严格意义上讲,神经系统不再具有临界态。
虽然在活体大脑中, τt 和 τs 的值有所不同,但它们并不随意改变。相反,正如最近发现的那样,τt 和 τs 通过一个简单的线性关系紧密地联系在一起。Fosque 和他的同事们表明,当他们模型的参数调整到“最大敏感点”时,这种线性关系就出现了,这意味着神经元对刺激最敏感。他们称这种状态为“准临界”:给定扰动、自发活化、尽可能临界。
研究小组得出了一个强有力的结论,即大脑活动的分支模式只有在没有外部刺激驱动的情况下,才是真正临界的,这一结论具有深远的影响。例如,大脑的不同区域,取决于它们的输入信息以及它们的功能,可能在距离临界点不同的距离运作。Fosque 和他的同事们的研究结果也与最近的发现相一致,即大脑皮层实际上可能是处于次临界态的[7,8]。
大脑处于准临界态带来的新问题
但是,为什么大脑动力学应该接近临界点呢? 是否是因为大脑的一些理想特征,诸如它对外部刺激很敏感,而且距离较远的区域会发生相互作用,从而使得系统远离临界点?答案可能是因为大脑动力学处于临界状态,该状态与其解决问题的能力纠缠在一起。可解与不可解问题用一个尖锐的边界来划分,最难解决的问题恰好位于边缘,即相变点[9]。对这一假说的明确结论将是理解生物计算中心原理的重要一步。
这项研究引发了其他有趣的问题。例如,抑制性神经元——那些降低目标活动的神经元——对临界动力学有何影响?这些细胞占大脑皮层所有细胞的五分之一,对防止失控性兴奋起着至关重要的作用。另一个问题是,是否存在不同形式的临界态,一种不能由分支模型和定向渗流捕获的临界态?
值得探索的一种可能性是,大脑可能徘徊在要么过度活跃状态,要么偶尔处于沉默状态这两者之间[6]。最后,神经元之间连接的几何形状和密度是如何改变临界指数的?模型通常假设随机的,密集连接的网络,导致平均场行为。非平均场行为是否在大脑中发挥作用,可能导致不同的幂律指数?随着研究逐渐揭示出非平衡统计物理学与大脑动力学之间有趣的联系,研究人员可以期待在未来找到这些问题和其他问题的答案。
原文地址:https://physics.aps.org/articles/v14/28
参考文献
1. L. J. Fosque et al., “Evidence for quasicritical brain dynamics,” Phys. Rev. Lett. 126, 098101 (2021).
2. J. M. Beggs and D. Plenz, “Neuronal avalanches in neocortical circuits,” J. Neurosci. 23, 11167 (2003).
3. N. Goldenfeld, Lectures on phase transitions and the renormalization group (CRC Press, Boca Raton, 2019)[Amazon][WorldCat].
4. V. Braitenberg and A. Schüz, Anatomy of the cortex: Statistics and geometry (Springer-Verlag, Berlin, 1991)[Amazon][WorldCat].
5. R. V. Williams-García et al., “Quasicritical brain dynamics on a nonequilibrium Widom line,” Phys. Rev. E 90, 062714 (2014).
6. A. J. Fontenele et al., “Criticality between cortical states,” Phys. Rev. Lett. 122, 208101 (2019).
7. V. Priesemann et al., “Spike avalanches in vivo suggest a driven, slightly subcritical brain state,” Front. Syst. Neurosci. 24 (2014).
8. J. Wilting and V. Priesemann, “Between perfectly critical and fully irregular: A reverberating model captures and predicts cortical spike propagation,” Cereb. Cortex 29, 2759 (2019).
9. P. Cheeseman et al., “Where the really hard problems are,” in Proceedings of the 12th International Joint Conference on Artificial Intelligence, IJCAI’91, Vol. 1 (Morgan Kaufmann Publishers Inc., San Francisco, 1991), p. 331[Amazon][WorldCat].
10. C. van Vreeswijk and H. Sompolinsky, “Chaos in neuronal networks with balanced excitatory and inhibitory activity,” Science 274, 1724 (1996).
本文来自微信公众号:集智俱乐部(ID:swarma_org),作者:Moritz Helias,译者:郭瑞东,审校:赵雨亭

