本文来自微信公众号:理念世界的影子(ID:spaceodyssey1968),本文首发于2020年6月25日,作者:洞穴之外,原文标题:《洞穴之外|运载火箭直径、规模与运载能力关系》,题图来自:视觉中国
一款火箭怎么从无到有?怎么得到火箭初始的直径、起飞规模?
火箭设计可以从理论推导而来,可以从现有继承而来,也可以从历史统计参考而来。
笔者从《世界航天运载器大全》上收集了177种火箭的基本参数,主要包括起飞质量、起飞推力、火箭长度、LEO运载能力等。通过对数据的分析统计,给出了运载能力与起飞重量、起飞重量与火箭等效直径、运载能力与等效直径的统计关系。
符号说明:
m:LEO运载能力;
M:起飞重量;
D:全箭等效直径。
等效直径定义
火箭构型种类繁多,除各子级直径相同的光杆构型可以直接给出全箭直径外,其他如直径不同的光杆构型,以及并联构型无法采用单一的直径描述。此处定义了一种全箭等效直径,定义为:与原火箭各子级等总体积、各芯级等总长的等效圆柱直径。
其中总体积是指所有子级体积(子级长度与截面积之积),它包括所有芯级和助推器;芯级总长是指所有芯级长度之和,因此不包括并联的助推器,也不包括整流罩。为简化,此处土星1、质子号、东方号等构型与其它火箭存在较大差异,不进行计算和纳入统计。
以长征三号乙为例,根据大全,助推器长度16.09m,直径2.25m,芯一级长度24.76m,直径3.35m,芯二级长度12.92m,直径3.35m,芯三级长度12.38m,直径3m,因此全箭等效直径为:
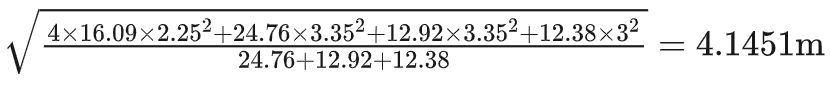
运载效率(运载能力与起飞规模之比)统计关系
统计 LEO 运载能力与起飞规模之比,即运载效率,有如下结论:
运载火箭运载效率线性拟合度较高,平均运载效率为0.0338(图1);
如仅计入100~1000吨起飞重量的中型运载火箭,平均运载效率为0.025(图2)。
并联构型中运载效率最大的为能源号,2200吨起飞重量,LEO运载能力100吨,运载效率达到0.0450;
串联构型中运载效率最大的为土星5号,2946吨起飞重量,LEO运载能力120吨,运载效率达到0.0407;
1000吨以内火箭,运载效率最大的为美国德尔它4M+(4,2),运载效率达到0.0378;
H2A,宇宙神5542,德尔塔4M,安加拉A5,法尔肯9重型,长征5号运载效率均排在前列(图3)。
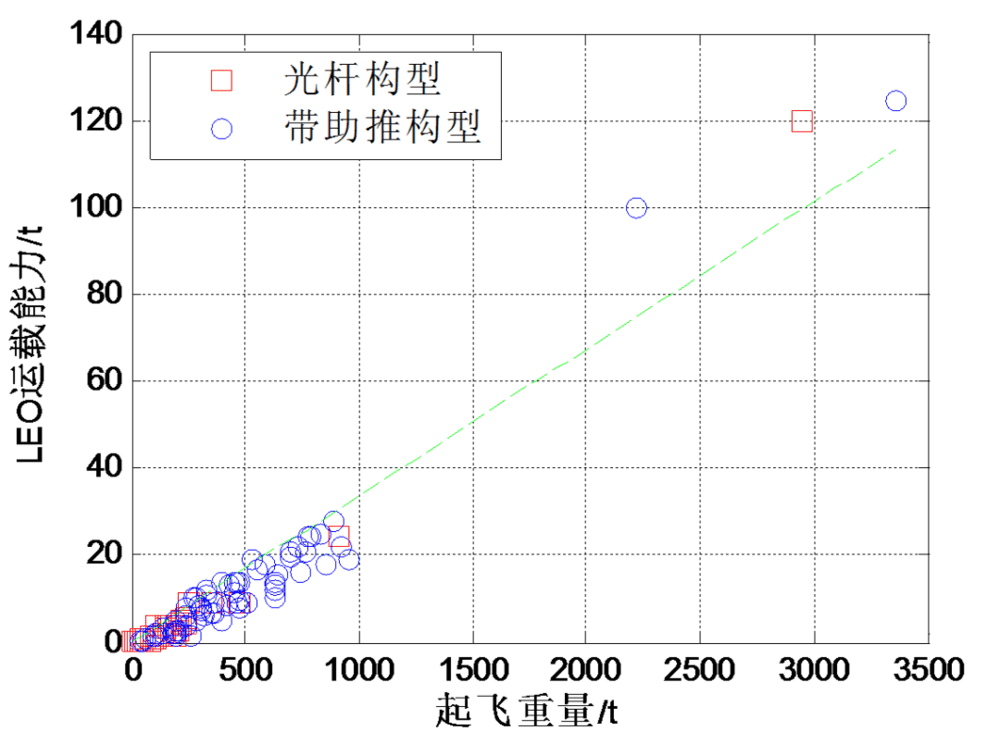
图1 运载能力与起飞规模关系(m=0.0338M,拟合优度R2=0.92)
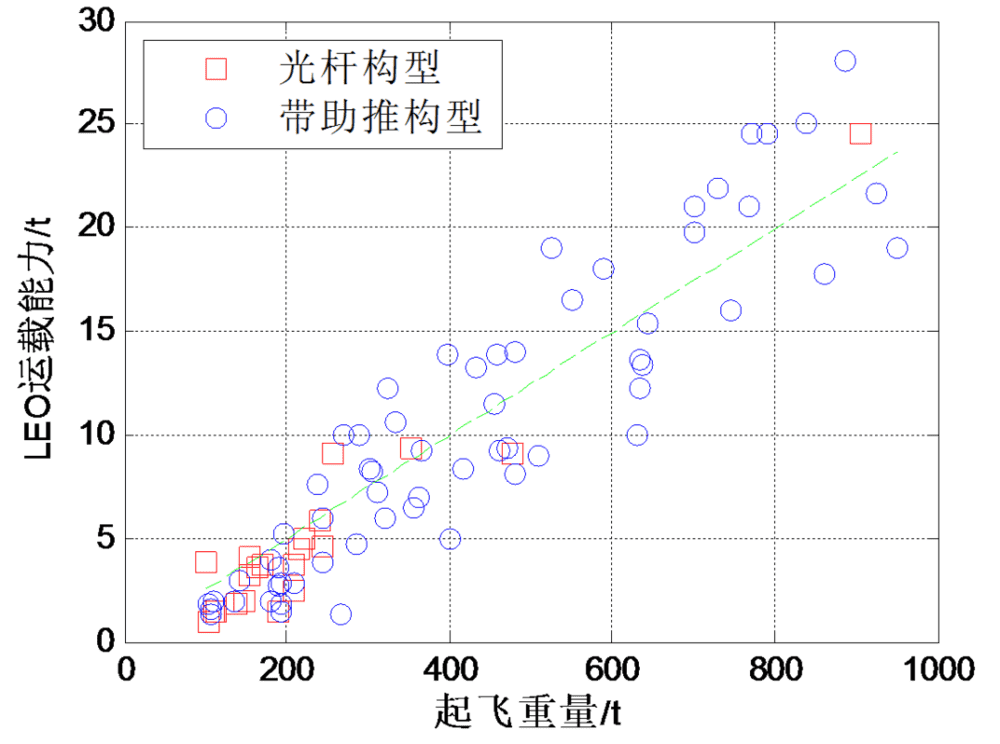
图2 运载能力与起飞规模关系,仅计入100~1000吨的火箭(m=0.025M,拟合优度R2=0.85)

图3 各型运载火箭运载效率
等效长细比(长度与等效直径)统计关系
统计火箭总长度与等效直径之比,即等效长细比(注意此处直径为等效直径,非芯级直径),有如下结论:
运载火箭等效长细比存在较大散布,拟合度不高,平均长细比为11.36;
等效长细比最大的为美国侦察兵B,达到25.38;
等效长细比最小的为能源号以及CZ-5B,分别为5.9和6.8。
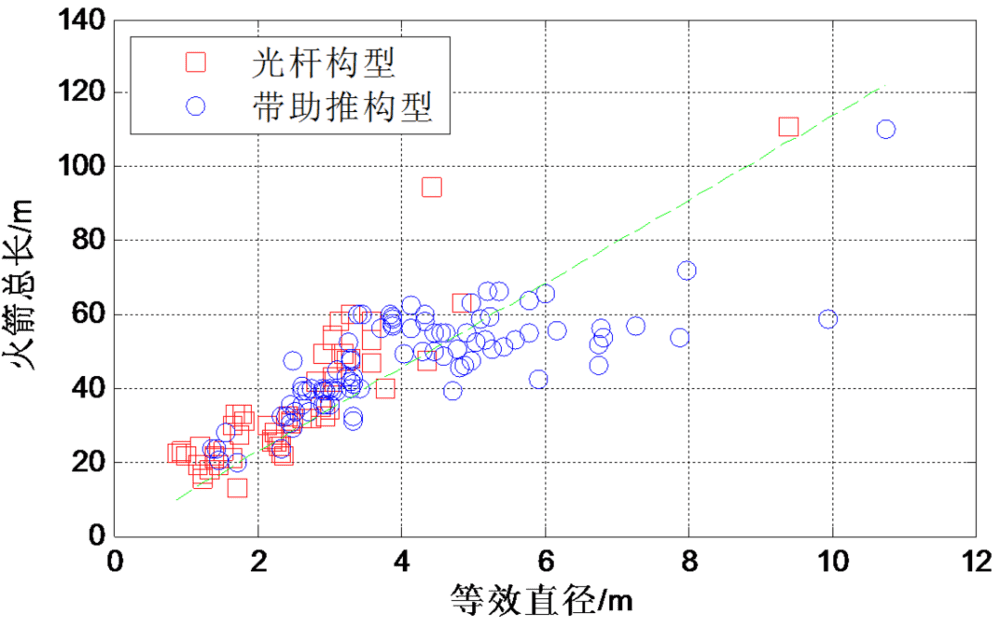
图4 火箭总长与等效直径关系(L=11.36D,拟合优度R2=0.46)
起飞重量与等效直径统计关系
统计起飞重量与等效直径关系,有如下结论:
起飞重量与等效直径平方呈正比关系,平均系数23.1,即 M=23.1D2,经比较平方比立方关系拟合度高。
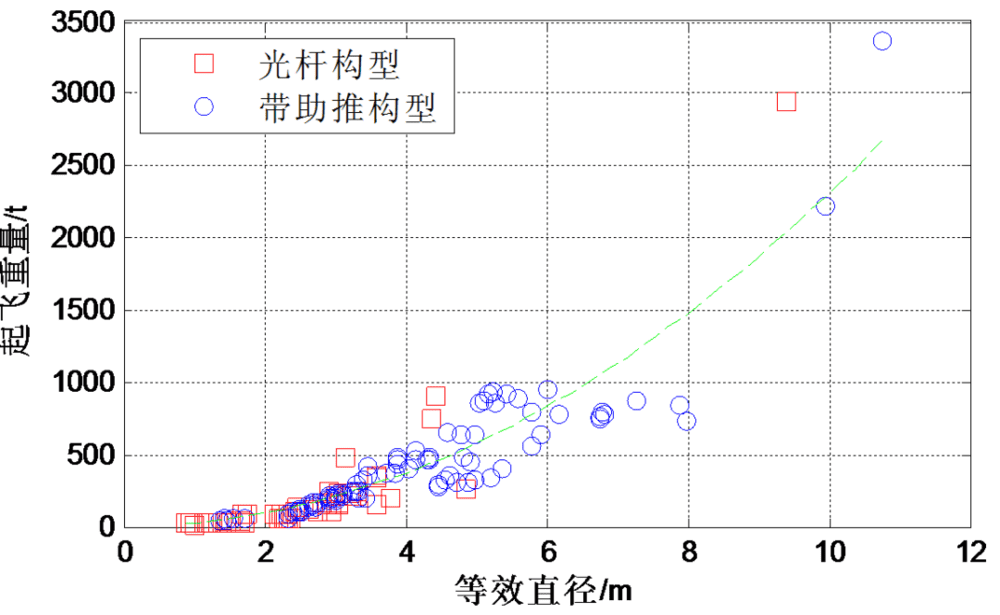
图5 起飞重量与等效直径关系(M=23.1D^2,拟合优度R2=0.85)
运载能力与等效直径统计关系
统计运载能力与等效直径关系,有如下结论:
运载能力与等效直径立方呈正比关系,平均系数0.1,即 m=0.1D3。
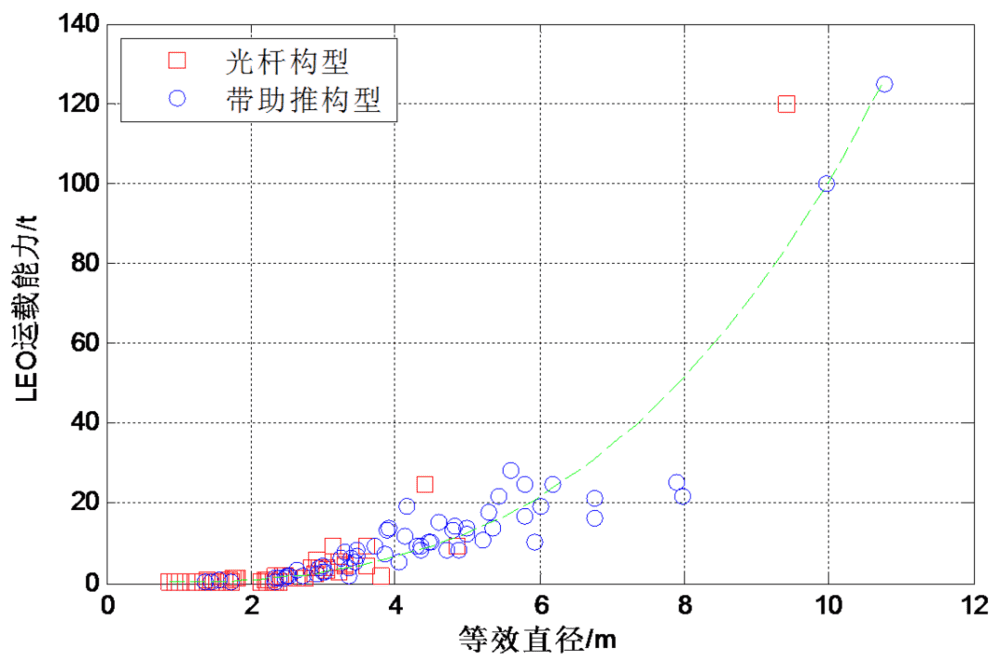
图6 运载能力与等效直径关系(m=0.1D3,拟合优度R2=0.89)
应用
采用上述统计公式进行初步估算,如某光杆火箭直径由3.35m增加到3.8m,从统计关系上看,火箭起飞规模可由260吨增加到330吨,LEO运载能力可由3.8吨增加到5.5吨,起飞规模增大1.3倍,运载能力增加1.5倍。
结论
通过对国际上177个火箭的直径、长度、规模、起飞重量、运载能力进行统计,得到以下统计结论:
LEO运载能力与起飞规模呈正比关系,m=0.0338M,即运载效率平均值为0.0338;
总长度与等效直径相关度不高,两者比值(等效长细比)均值为11.36;
起飞重量与等效直径平方呈正比关系,M=23.1D2;
运载能力与等效直径立方呈正比关系,m=0.1D3。
参考文献 :《世界航天运载器大全》编委会编. 世界航天运载器大全[M]. 中国宇航出版社, 2007.
本文来自微信公众号:理念世界的影子(ID:spaceodyssey1968),作者:洞穴之外

