之前在《火箭是怎么飞到目的地的:生活化描述》中讲了GNC的一般概念,在《火箭是怎么飞到目的地的:物理描述》文中介绍了制导。本篇主要讲姿控,数学公式较多,慎入。
由开环到闭环
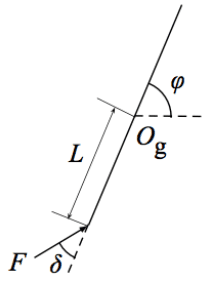
如上图的火箭,重心位于图中Og处,忽略气动力、阻尼等,则仅有发动机摇摆(摆角为δ)可让火箭转弯,由转动惯量*角加速度=外力矩,运动微分方程为:
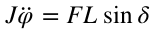
进一步,将发动机摆角线性化,方程写为:

从这个二阶微分方程开展探讨,可将输入输出画成框图:
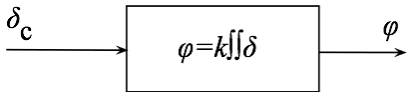
假设所需的姿态角规律为:
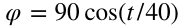
则给定发动机摆角:
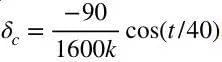
这时,得到的姿态角曲线与需要值的偏差是:

姿态角误差较小,即在给定摆角下,可以实现预定的姿态角。
现实都是有干扰的,真实模型可能是这样的:

假设干扰为最大值0.001的平均分布函数,则给定上述发动机摆角时,偏差曲线见下图,累积误差已经不可接受。
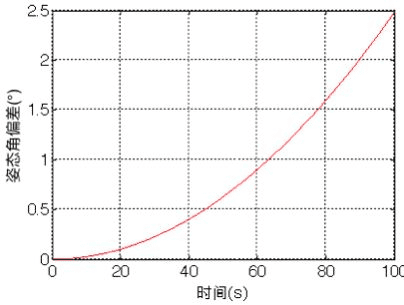
怎么办?采用反馈控制。
由直连到网络
反馈控制就是将输出与需要的输入比较,求差后计算出发动机摆角,从而达到需要的姿态角。
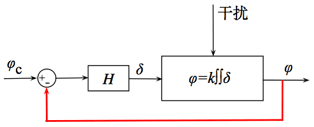
求差之后直接作为发动机摆角感觉总是有点别扭,假设有个转换函数H,只是暂时不知道取什么,在没有思路时就先用1试试(还记得《设计和仿真有什么区别?》说的设计和仿真吗?设计没有思路时,先仿真一下找找感觉)。
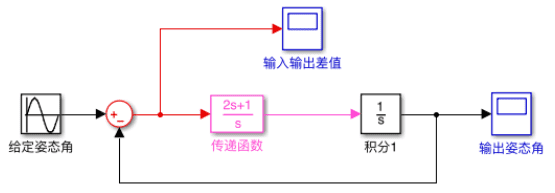
由于存在回环,方程不那么容易求解了(譬如采用Laplace变换求解,会发现最后的解涉及一个卷积计算)。这里直接用matlab的simulink求解,计算时假设k=1,另外积分运算Laplace变换后就是1/s。

图中蓝色模块为输出的显示,可以看出,输出基本接近输入,误差在0.15°范围内。
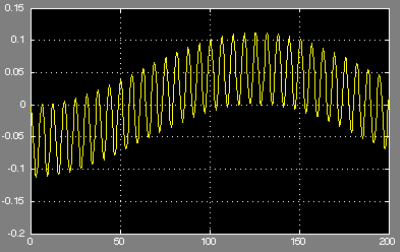
将带反馈的闭环框图与之前开环的框图比较。
开环中,发动机摆角δc必须事先从输入的姿态角计算得到。而在闭环中,事先根本不需要知道输入姿态角是什么。
此处H=1,也就是给定姿态角和输出姿态角的差值就是发动机摆角。
两个根本不相关的东西怎么就靠一根线联系到一块儿?笔者一直想不出一个直观的解释。
连根线,感觉一切就迎刃而解了。莫非这就是《设计和仿真有什么区别?》那条价值9999美元的线?
此例中摆角有些振荡,还有很多其他例子摆角直接发散,如要设计出稳定、平稳的摆角,还得再研究研究。首先引入几个名词。
几个名词:
传递函数:指零初始条件下线性系统响应(即输出)量的拉普拉斯变换与激励(即输入)量的拉普拉斯变换之比。传递函数是复变量s的有理分式。
零点:有理分式中分子多项式等于0时的根。
极点:有理分式中分母多项式等于0时的根。
开环传递函数:人为断开反馈后的传递函数。
写出输出对输入的传递函数:
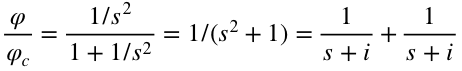
公式的右半部分可以写成如下形式,这里pj为极点,zi为零点。
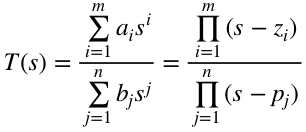
闭环系统输出稳定要求极点全部在左半平面(实部全部小于等于0),只要有一个实部大于0,系统频域就不稳定。而在本例中,实部正好等于0,此处是一种临界稳定状态,其稳定性需要更多信息进行判断。
为了让振荡衰减得快一些,可以增加传递函数H,这个传递函数一般称为增益和网络,增加后闭环传递函数为:
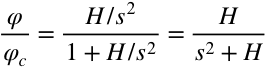
如果H=2s+1,两个闭环极点均为-1。如下图所示,振荡已经没有了,而且误差降低到0.06°。
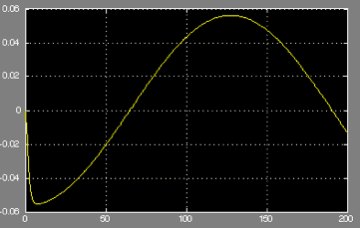
由加法到乘法
现在问题是,计算闭环极点很麻烦,闭环传递函数为:

而真实的动力学模型G(s)极为复杂,这时的H(s)难以设计。因为在多项式分解中,加法是个很讨厌的东西,它改变了原有方程的解,而乘法不会。如s2=0的解与s2+1=0完全不同,而与之相比s2*(s+2)=0只是多了一个解而已,原有解没有变。
如何处理1+GH?能不能从GH本身反映出系统的特性?
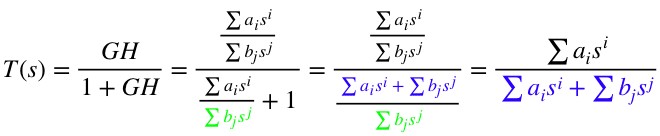
上述公式中,从标蓝色处看,闭环传递函数的极点等价于1+GH(s)的零点,还是有个讨厌的加法。
再看看标绿部分,有个好消息,即使有1+,GH的极点并没有变化!即1+GH和GH的极点一致。终于摆脱加法了!
可是,我们要的是零点,给极点有什么用?这里不做太多描述地引入辐角原理,它架设了极点和零点间的桥梁。这才是《设计和仿真有什么区别?》那条价值9999美元的线!
辐角原理:对于函数F(s),如果复平面上一条封闭曲线内包含了它的Z个零点、P个极点,则s沿封闭曲线顺时针转一圈时,F(s)映射到复平面上的曲线绕原点逆时针转过的圈数R=P-Z。
很拗口,直接上案例:
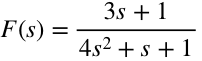
它的零点为-1/3,极点为-1/8(1±sqrt(15)i)。下图中o为零点,x为极点,左侧为s转一圈,右侧为F(s)曲线。
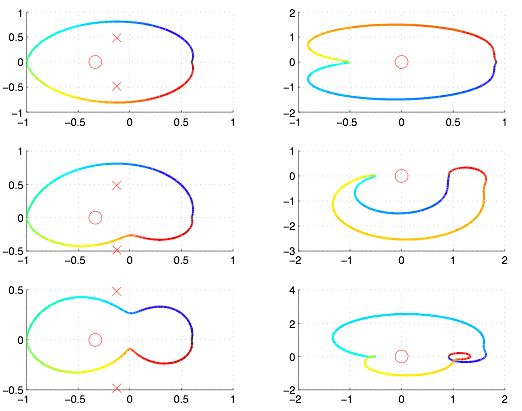
上图中,极点比零点多1个,右图曲线绕零点逆时针转了一圈;
中图中,极点与零点个数相同,右图曲线不过零点;
下图中,极点比零点少1个,右图曲线绕零点顺时针转了一圈。
因此,理一下逻辑:
闭环系统稳定
1+GH的零点实部小于0
利用: 1) 封闭曲线画在右半平面(从而无零点)
2) 曲线内有1+GH的P个极点
沿曲线走时,1+GH(s)曲线逆时针绕0点正好为P圈
利用: 1) 1+GH的极点和GH极点相同
2) 1+GH平面内逆时针绕0点,等价于GH逆时针绕(-1, 0)点
因此,闭环系统稳定等价于在右半平面画个封闭曲线,开环传递函数(GH)映射到复平面上的曲线逆时针绕-1点转P圈,此处P为GH的极点个数。
终于没有加法了。
由数圈到穿越

我们需要一个什么样子的封闭曲线呢?如图,虚轴从-∞到+∞,之后再顺时针兜一个无穷大的半圆。
这里对如下两个问题不做过多阐述:
如果零点在虚轴上怎么办?兜一个无穷小的半圆绕过去,这个半圆对应的GH(s)性质此处不细研究;
任何物理系统在无穷大频率处的响应都为0。因此,兜无穷大半圆时,GH(s)=0,Nyquist曲线都是始于0,终于0的曲线。
现在进一步简化了,不再去费心找什么封闭曲线,只需将F(s)中的s从-jω走到+jω即可,这就是Nyquist图。
直接看这个公式:
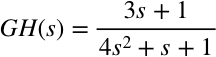
的Nyquist图吧,它在右半平面无极点,Nyquist图不过-1点,因此形成的闭环系统也是稳定的。也就是不用计算,就可以肯定(4s2+s+1)+(3s+1)=0的根实部均小于0。
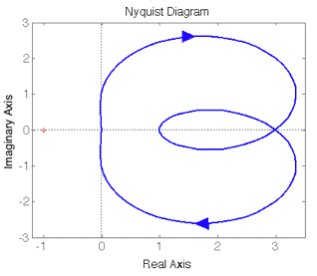
再来一个例子,这里Nyquist图绕原点两圈,但由于F(s)在右半平面有两个极点,闭环系统还是稳定的
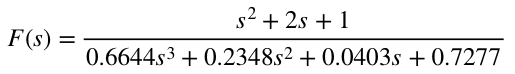
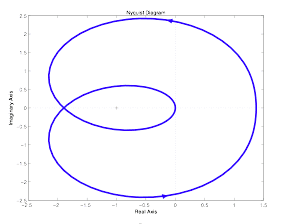
数圈比较麻烦,来三个技巧:
F(jω)和F(-jω)共轭,Nyquist图均关于横轴对称,因此只需将F(s)中的s从0ω走到+jω即可,再将数出来的圈数乘以2;
由于关于横轴对称,上半平面有半圈,下半平面必有半圈,因此圈数等价于穿过横轴的次数;
曲线总是从0点出发并闭合,在(-1, 0)点右侧,无论穿横轴多少次,对总圈数没有影响(当然,直径小于1的圆内更不用数,这个特性在Bode图中会用到)。
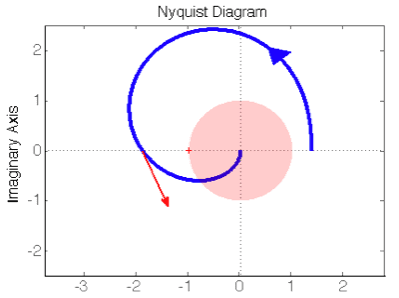
下图画出它的半部分,它在-1点左侧向下穿越横轴1次,右边穿越次数不用数,因此总圈数为1x2=2圈。
Nyquist图建立了从开环到闭环传递函数的桥梁,不需要求解闭环系统的根,直接从图形和开环极点数目即可判断稳定性。这里的困难在于图形的绘制。如下图,蓝色和绿色分别为G和H的Nyquist图,从中能简单画出红色的GH吗?恐怕难。

由乘法到加法
Bode将上图表述为两张图,一是幅值对数20lg|GH|,二是GH的辐角。对于G和H的乘法,取对数和辐角后,全部转化为加法。如下图,从蓝色的G和绿色的H,叠加即可得到GH。
有了G的Bode图,大脑中再有几个典型传递函数的Bode图,就可以直接在大脑中设计增益和网络了。

判读方法也未变:
Bode图幅值小于0dB,它代表在Nyquist图的以0点为圆心,直径小于1的圆(见前面的图),它肯定在-1点的右侧,因此对圈数无影响;
幅值大于0dB,而且辐角等于180(或-180)度时,代表在Nyquist图上穿越了横轴负半轴,仍可以按上下穿越次数判读。

实际上我们在用Bode图时,使用的是更为蜕化的情况,即工程中如果G, H的极点实部均小于0时,闭环系统稳定要求Nyquist图绕-1点0圈,此时稳定性等价于:当幅值大于0dB时,辐角图180度的上穿越次数等于下穿越次数。
总结
梳理一下逻辑:
由开环到闭环。在有干扰情况下,开环如误差过大,只能诉诸于闭环;
由直连到网络。直接闭环反馈,输出特性未必好,需要增加增益和网络,使闭环系统极点位于复平面左侧;
由加法到乘法。求闭环极点涉及一个加法,使得原传递函数信息无法应用,辐角原理将极点、零点数目联系起来,消除了此加法环节;
由数圈到穿越。稳定性转化为开环传递函数的Nyquist图绕-1点圈数,数圈较为复杂,而圈数等价于穿越-1点左侧横轴次数;
由乘法到加法。Nyquist图不好画,采用Bode图,只需要将所有传递函数叠加起来即可,而判读时仍只需计算穿越次数。
以上就是Bode图的解释以及判读方法。方法来来回回变换多次终于达到目的,非常巧妙,它是任何一本经典控制原理书中都会有的内容,产生于1932年(电子计算机出现之前,有了计算机后,我们的动手能力上升了,但动脑能力有可能是下降了)。
本文来自微信公众号:理念世界的影子(ID:spaceodyssey1968),作者:洞穴之外

