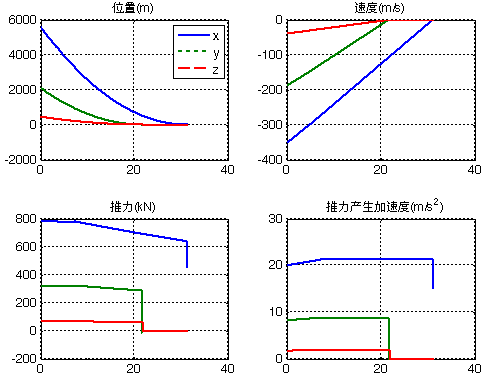
如图,怎么做到的?

图/SpaceX
现在我们都知道,发动机靠的是Tom Muller,在TRW干了15年,TR-106发动机负责人,然后,被Musk挖走了。
控制靠谁呢?在领英上有这么一组简历:剑桥本科和硕士,麻省博士,随后在JPL干了4年火星着陆。然后,也被Musk挖走了。
他就是Lars Blackmore,SpaceX火箭着陆工程负责人,入轨火箭一级着陆第一人。看起来定语也不少哦,这是因为航天飞机轨道器和助推器都被回收过,而蓝色起源又抢了个亚轨道一级回收。只是这里定语虽然多,但却分量最重,因为很难且意义重大。

图/LinkedIn
Lars Blackmore曾撰文说:SpaceX使用CVXGEN生成定制的飞行代码,采用高速在线凸优化算法。
凸优化是啥?
问题模型和简化
忽略地球曲率,忽略大气阻力,假设发动机比冲恒定,第一步不考虑横向运动,只考虑垂向,可将问题描述为:
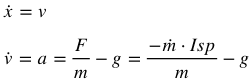
这里F为发动机推力,模型简化为:通过流量(ṁ)调节,实现位置为0时,速度为0。
这里流量怎么调节有无穷多可能性,正是《设计和仿真有什么区别?》中所说的无穷多个自由度。加载个遗传算法、粒子群算法包暴力寻优?不会有好结果。
做出一个解析解?从上式可以积分出速度,即我们都知道的齐奥尔科夫斯基定律。但已经没法再进一步写出位置公式来。那就进一步蜕化。
假设为常流量,问题转化为了流量为多少的问题,只有一个优化变量。但此时仍写不出位置解析公式,难以进行一般结论分析。
假设为常加速度呢?通过不断降低发动机推力,与箭体重量匹配,达到常加速度下降,此时公式可写为:
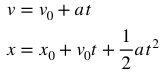
从双过零条件,即末位置和末速度均为0,可以解出着陆时间t=-2h/v0,过程中加速度为:
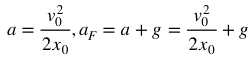
从上式可知,对于简化模型,给定初始位置和速度,存在恒加速度,可以实现双过零。比想象的好,因为之前还担心找不到解呢?
采用文献给出的Falcon返回参数(r0=[5582 2100 450]; v0=[-353 -190 -40]; m0=38963;),此处只考虑x方向,从图中可以看到在可变推力下,位置和速度同时到达0。
从图中也可以看出,返回初始条件的给定比较讲究。如图,推力正好从800kN左右调节到650kN,而对应Merlin1D发动机推力调节范围为592~845kN。
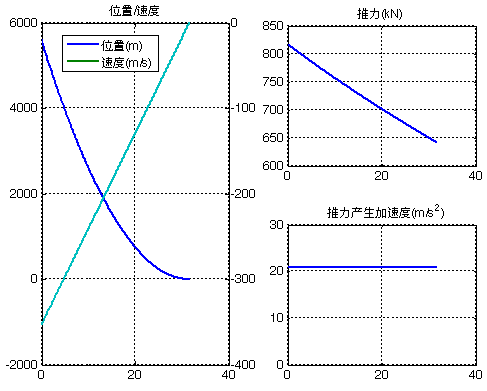
简化模型在干扰下的适应性
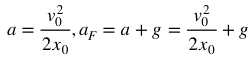
上图这个公式中,如果只用初始点的位置和速度,是无法适应干扰的。观察此式发现,对于任何时刻,都可将此时刻作为起始时刻,都可以重新计算一个加速度,这时候,算法就具备了一定的干扰适应能力。
如发动机点火时推进剂剩余量多500kg,同时发动机推力比指令值少5%。计算表明,此偏差下仍能双过零,只是着陆过程中给出的指令已经不是常值加速度了。但总体而言,一维情形下的返回是件简单的事情。
三维情况
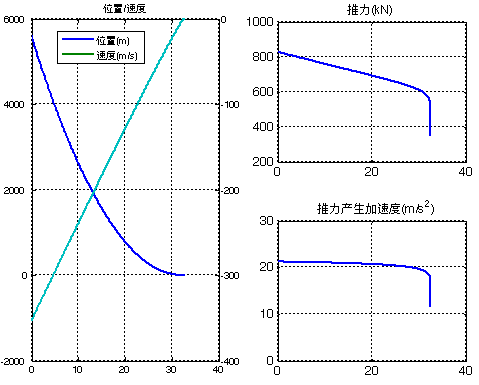
仍采用公式a=v0^2/2/x0,三个方向分别施加。采用文献参数(r0=[5582 2100 450]; v0=[-353 -190 -40]; m0=38963;),可以看到在位置和速度同时到达0。图中的推力产生加速度在初始时刻不是常值,这是因为发动机推力存在最大值限幅。
从图中可以看出,Y/Z向速度比X向先到达0。这是靠合理的XYZ位置、速度起始值组合保证的,在算例组合下,t=2r0/v0=[31.6261 22.1053 22.5000]s。
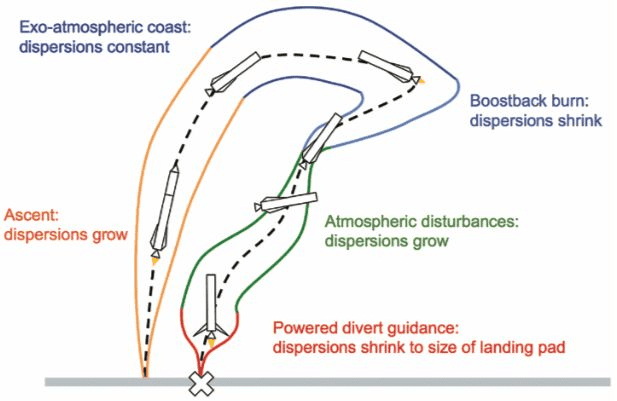
这个组合要求非常高,这也意味着Falcon返回的气动减速段,栅格翼一定不仅仅在调姿态和减速,同时也在进行制导,为反推点火点寻找较好的位置和速度组合。
如果点火时条件存在偏差怎么办?以速度为例,假设反推点火时x向速度仍为-353m/s,若:
Y/Z向速度偏小,此时Y/Z方向需要调节时间增加,若超过X向时间,返回时必然大幅偏离返回点。如Y向速度为设计值的60%,计算表明落点偏离42m;
Y/Z向速度偏大,需要更大的调节推力,从而造成推力限幅,使得X向无法达到需要加速度。如Y/Z向速度为设计值的110%,计算表明火箭将以100m/s砸向地面。
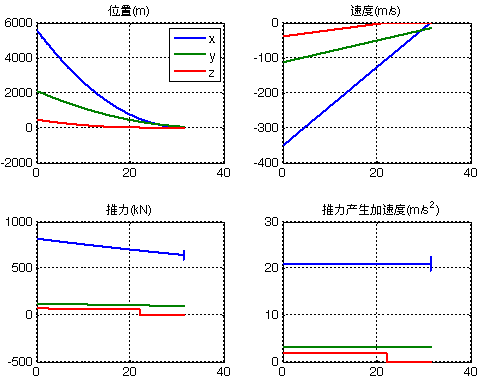
Y向速度为设计值的60%,落点偏离42m
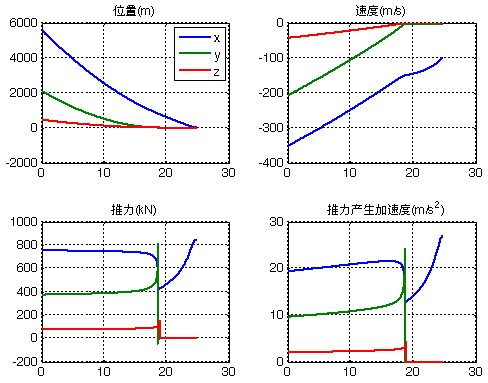
Y/Z向速度为设计值的110%,落地速度100m/s
凸优化
上述例子中,偏差大的原因是算法中对于X/Y/Z三向独立考虑,没有估计它们之间的联系。应该是有办法可以处理这种联系的,只是笔者对GNC实在不熟悉,就直接转向Lars Blackmore在文中所说的凸优化吧。
推荐文献:
[1]Behçet Açikmeşe, Lars Blackmore, etc, Enhancements on the Convex Programming Based Powered Descent Guidance Algorithm for Mars Landing, 2008
[2]Lars Blackmore, Behçet Açikmeşe, etc., Minimum-Landing-Error Powered-Descent Guidance for Mars Landing Using Convex Optimization, 2010
[2]张志国等,火箭垂直回收着陆段在线制导凸优化方法, 2017
方法其实很简单和程式化,先将原始模型:
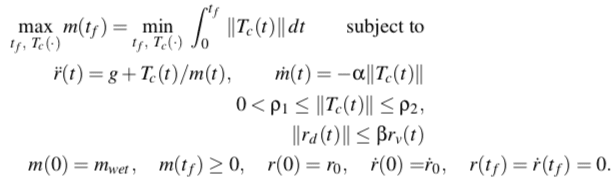
转化为如下凸模型:
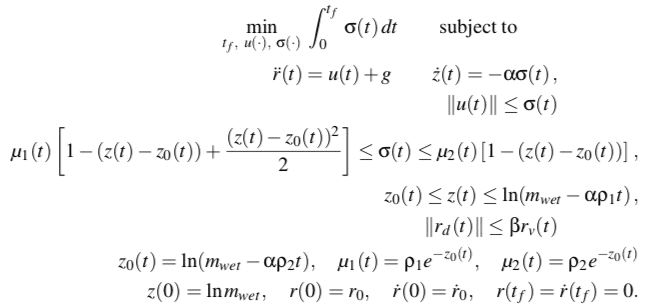
进而离散:
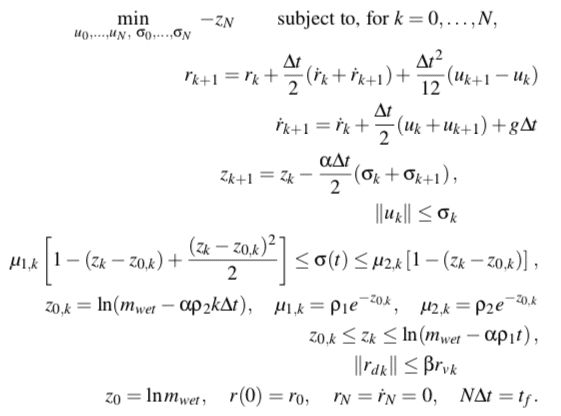
对照上述离散模型,可以直接写出计算程序。
在设计工况下的返回情况见下图,与之前算法结果最大不同在于,推力大小不再连续变化,而是在最大、最小推力处切换,即bang-bang控制。
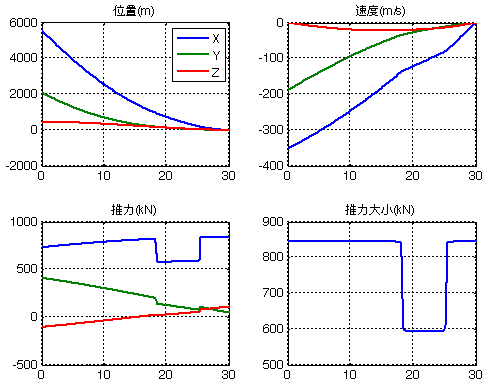
对于之前的Y/Z速度增加10%,或Y速度降低40%工况,采用凸优化算法仍然可以得到较好的结果,即算法对偏差适应能力更大。
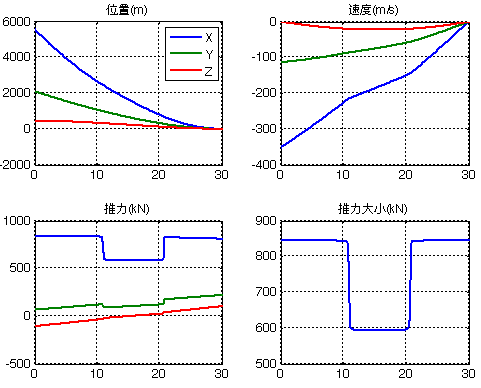
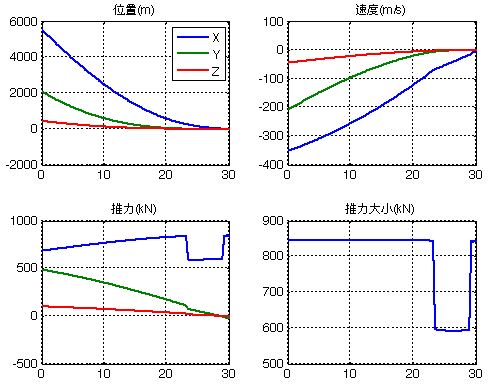
另外,与之前比,采用凸优化后,Y/Z速度趋向零的过程好像稍慢,可能导致箭体落地前有点倾斜,笔者觉得再加一些凸约束即可,就不一一尝试了。
在真正飞行中,在每一个制导周期都需要优化一次,获得当前推进力和方向,随后按此值推进,并在下一个制导周期重新计算。凸优化算法的优点在于,可在确定时间内给出满足指定精度的优化解,从而具备在线求解可能性,如SpaceX使用CVXGEN生成的凸优化算法实现在线实时求解。
看来在前人现成理论和工具包面前,火箭返回看起来不难嘛。但别忘了,以上只是最简单情况下的示例。Blackmore曾说:地球大气密度是火星100倍,气动力成为最大的变量而不是干扰,在地球上返回是一个复杂的问题。
就像足球里的吊球,接球的人训练时也许可以做到,但在比赛的高对抗中,就未必那么容易了。好多时候,说简单、说难都没什么意义,只有干了才知道。
本文来自微信公众号:理念世界的影子(ID:spaceodyssey1968),作者:洞穴之外

