火星自古以来就吸引着人类。这颗红色行星的逆行为托勒密的太阳系模型提供了动力;千年以后,开普勒的行星运动定律是他持续了大约18年的“火星大战”的结果;上世纪初,天文学家Percival Lowell观测到的火星“运河”为人类的想象力插上了翅膀;在过去的30年里,为了研究火星的表面和大气,人类多次成功尝试登陆火星。
时间兜兜转转到了2020年7月,在前后10天内,人类飞行器扎堆向火星进发。7月20日阿联酋的“希望号”火星探测器最先启程;7月23日我国的“天问一号”开启了前往火星的史诗级征程;7月30日,美国“毅力号”火星探测器也迈向了深空。
很多公众号,已经给我们普及了如下航天知识:
地球火星每26个月接近一次;
每26个月有次机会去火星最省能量;
这条最省能量的路径是霍曼转移轨道(霍曼变轨);
沿着这条轨迹要飞行7个月才能到达火星。
如下美图直观地揭示了以上知识:
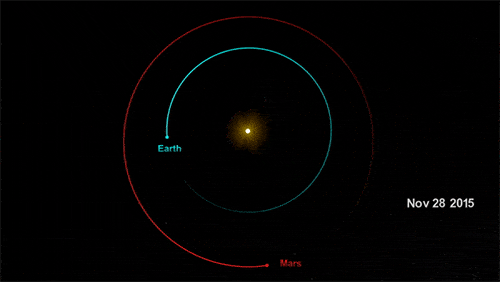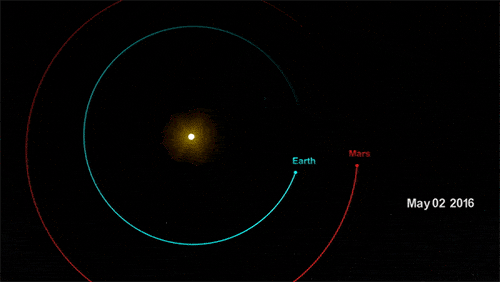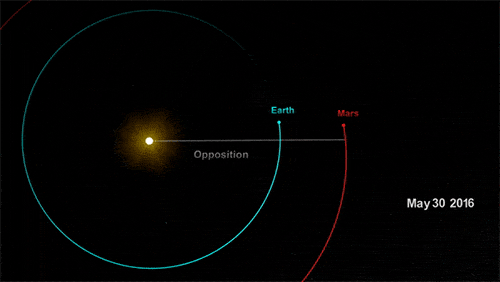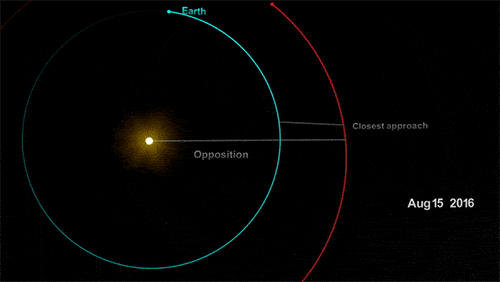
图 地球火星距离(来自NASA)

图 霍曼转移轨道(来自NASA)
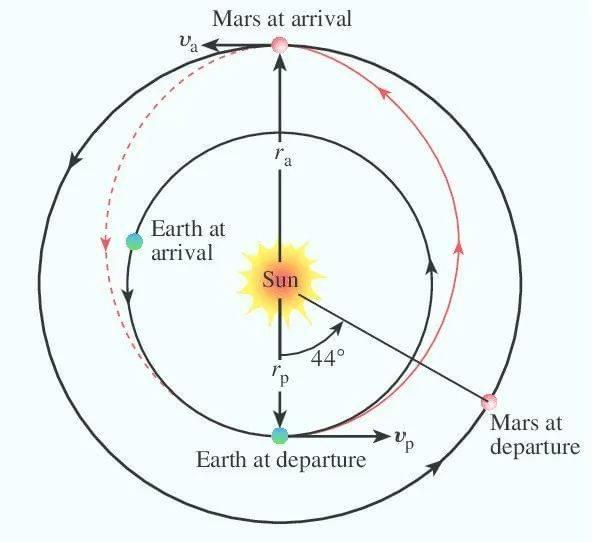
图 地球-火星轨道描述(来自文献1,注意图中的44°)
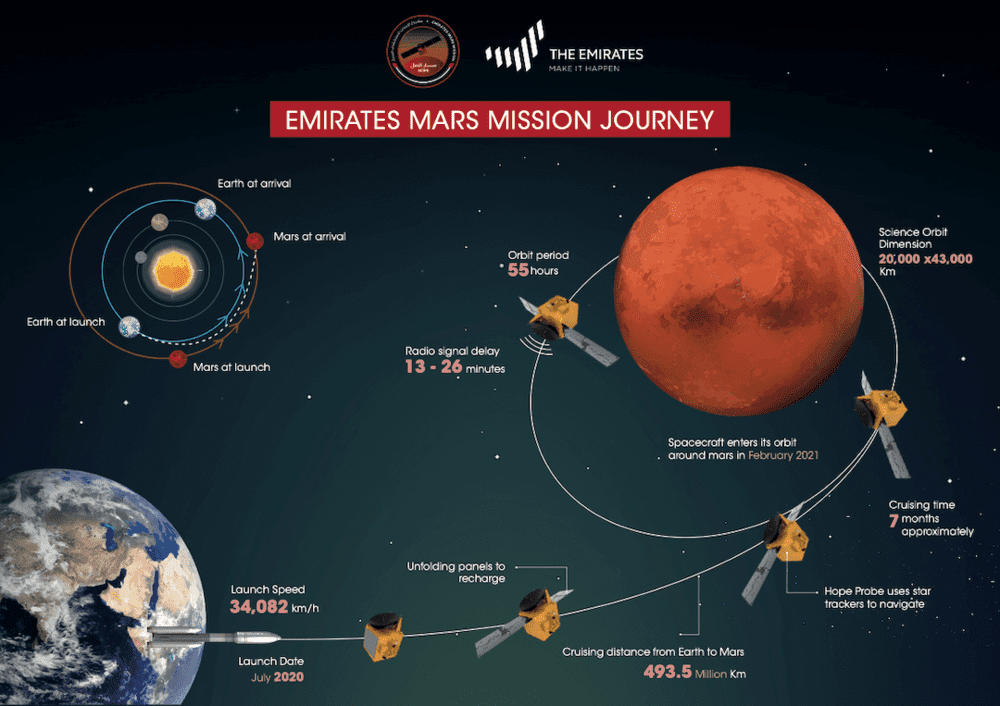
图 “希望号”火星探测器的旅程
从图中可以看出,走霍曼转移轨道,为了在轨道远地点与火星相遇,出发点地球、火星与太阳连线的夹角为44°。
但笔者手欠算了一下,发现2020年7月20日左右,地球、火星与太阳连线夹角只有30°,7月30日为26°。除非提前1个月半,即6月6日左右,夹角才为44°。
python程序(缺哪个模块pipinstall即可)
from astropy.time import Time
from jplephem import Ephemeris
import de421
from math import *
tjd=Time('2020-6-6').jd
eph=Ephemeris(de421)
pe=eph.position('earthmoon',tjd).reshape(1,3)[0] # 地月系公共质心离地心约4671公里,影响可以忽略
pm=eph.position('mars',tjd).reshape(1,3)[0]
ps=eph.position('sun', tjd).reshape(1,3)[0]
p1=pe-ps; p2=pm-ps
r1=sqrt(p1.dot(p1)); r2=sqrt(p2.dot(p2))
theta=acos(p1.dot(p2)/r1/r2)*180/pi
print(theta)
自然地,笔者想解决如下几个疑问:
这些探测器走的真的是霍曼转移轨道吗?霍曼变轨是不是最优的?有无证明?
轨道差异是因为偏心率、轨道倾角影响?还是因为地球和火星引力场影响的结果?
于是就有了此篇调研。
到火星走的是什么轨道?
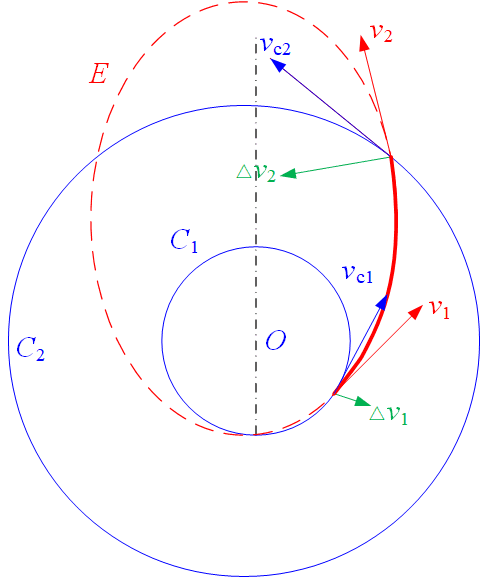
图 变轨示意图
如上图,为从轨道C1到达轨道C2,至少需要两次点火,第一次点火将圆轨道变为轨道E,在轨道E与轨道C2相交时第二次点火。
这条新轨道E的方程写为r=p/(1+e cos f)。新轨道需要通过r1和r2,因此r1和r2需要包含在轨道半长轴和半短轴之间,这就给出了轨道E的约束方程:
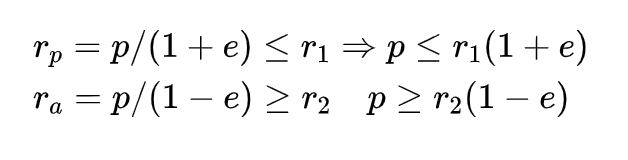
这个约束可以用如下图形表示,变轨轨道可以为椭圆、抛物线或双曲线轨道,但必须在两条直线所包含的区域内。
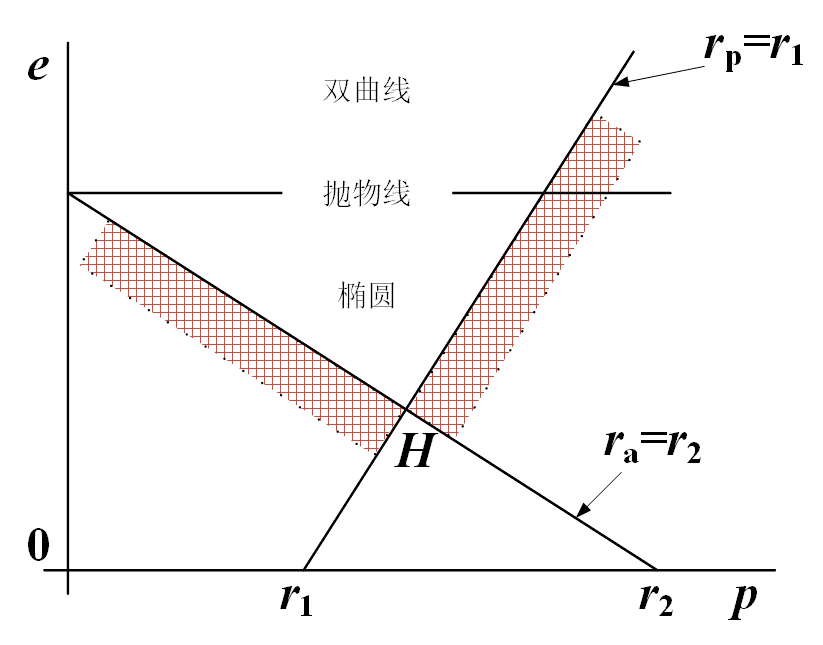
图 变轨轨道可行域
写出每次变轨需要速度增量,并将总速度增量∆v∑=∆v1+∆v2对e求导可以得到:
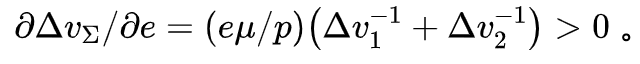
因此变轨所需速度增量随着偏心率e增加递增,在可行域的H点e最小,此时变轨所需总速度增量最小。H点对应ra=r2,rp=r1,即变轨轨道与轨道C1和C2均相切,这就是霍曼转移轨道。

对于霍曼变轨,转移轨道时间t12等于过渡椭圆轨道周期的一半:
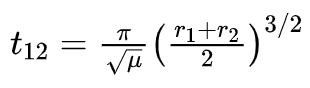
根据火星与太阳平均距离1.52AU(天文单位),以及地球轨道半径1.5e8km,计算得到轨道转移天数为259天。
根据这个时间段内天体所走距离,可以计算得到提前角(出发瞬时天体与中心连线夹角):
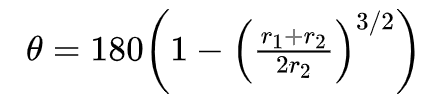
代入r2/r1=1.52,计算得到提前角为180*(1-((1+1.52)/2/1.52)^1.5)=44.149°。
从上可以得到如下结论:
对于共面圆轨道,采用两次脉冲点火(推力、比冲无穷大),霍曼变轨最省能量;
如果将地球和火星视为共面圆轨道,采用霍曼变轨登陆火星,提前角为44.149°。
为什么集中在2020年7月发射?
地球轨道偏心率0.0167,火星轨道偏心率0.0934。火星近日点距离2.0662e8km,远日点距离2.4923e8km,如果再考虑火星与黄道1.85°的交角,不可能进行真正的霍曼转移,而只能是类霍曼转移。
这种转移太过复杂,很难下手,可以先将问题蜕化一个维度:给定出发时间和到达时间,这时出发位置、到达位置都是确切的(查询行星星历),求解这两点间轨道。此时问题转化为两点边值问题。
这个问题就是Lambert问题或高斯问题,它产生于18世纪,其初衷是通过观测来确定行星轨道,高斯使用这种方法确定了谷神星轨道。
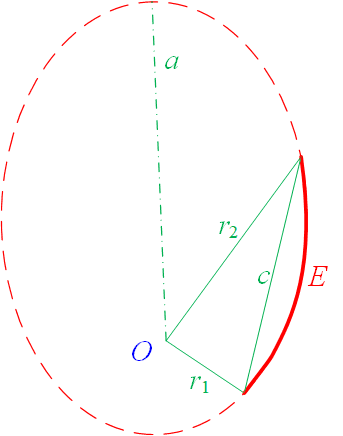
图 Lambert问题
这里存在时间不利于求解,Lambert飞行时间定理表明:
双脉冲变轨所需时间仅仅依赖于转移轨道的半长轴a,两个变轨点到中心天体距离和r1+r2,以及两个变轨点间的直线距离。即:
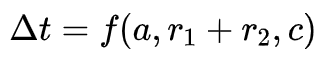
这个定理表明,转移轨道飞行时间仅与两点位置,以及轨道半长轴有关,而与其它轨道参数如偏心率无关,从而将问题解耦。再进一步计算出两点速度和需要速度增量。

以出发时间和到达时间为坐标,逐个求解Lambert方程,得到需要速度增量见下图所示。这个图又被成为猪排(Porkchop)图,它通过暴力扫描出发日期和到达日期得到,可以帮助任务设计者规划两个天体之间的转移轨道,是去往火星的第一个菜单项。由于轨道偏心率和倾角缘故,图形大体在每个周期内模式重复,但又不尽相同。
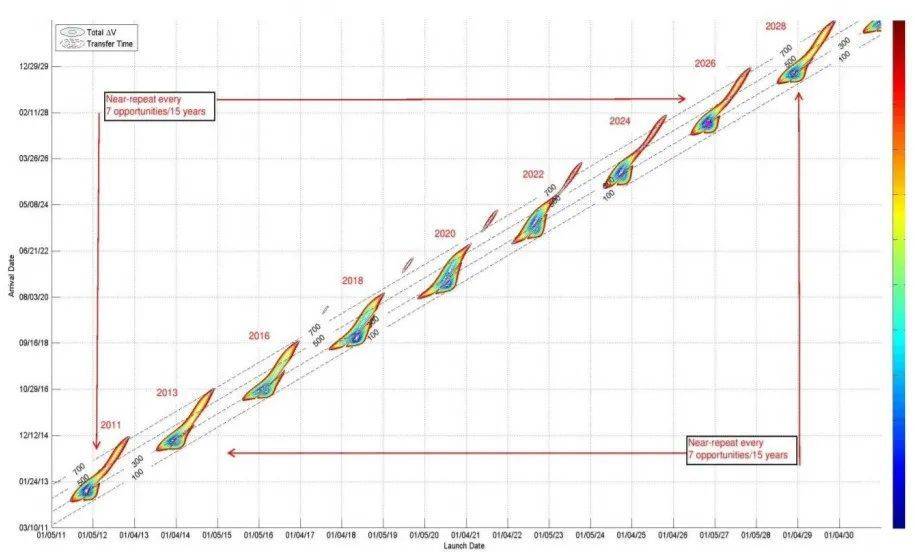
图 地球-火星到达Porkchop图
近1年时间内总需要速度增量和飞行时间图形见下所示。图中红色等高线为需要总速度增量,蓝色代表飞行天数。从图中可以粗略读出,一种较省能量的配置是2020年7月23日出发,约2021年2月13日到达,所需速度增量最小,飞行205天。
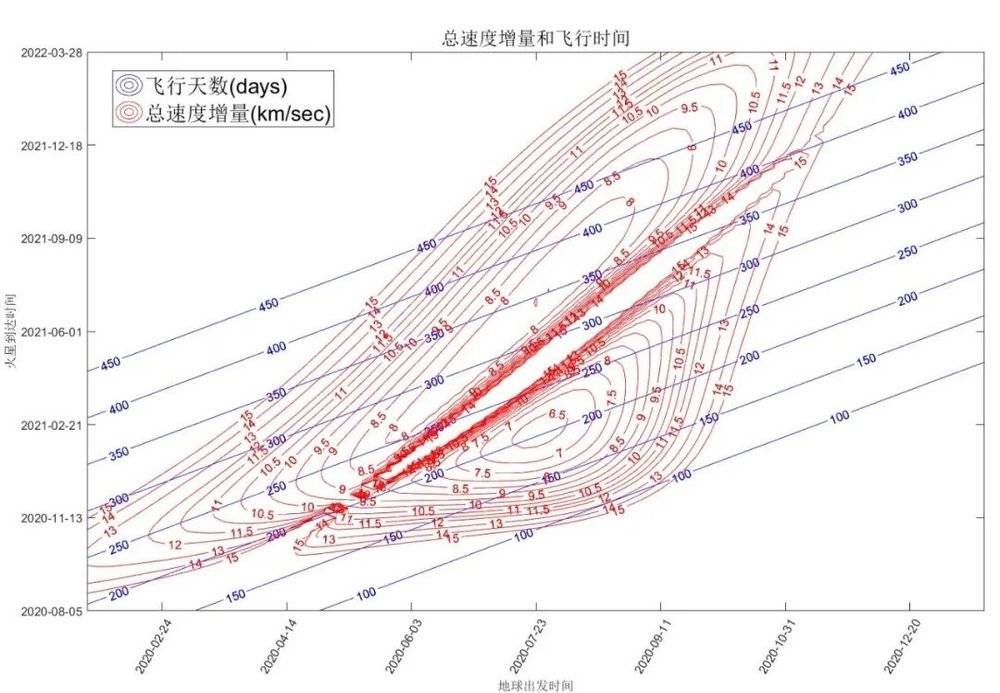
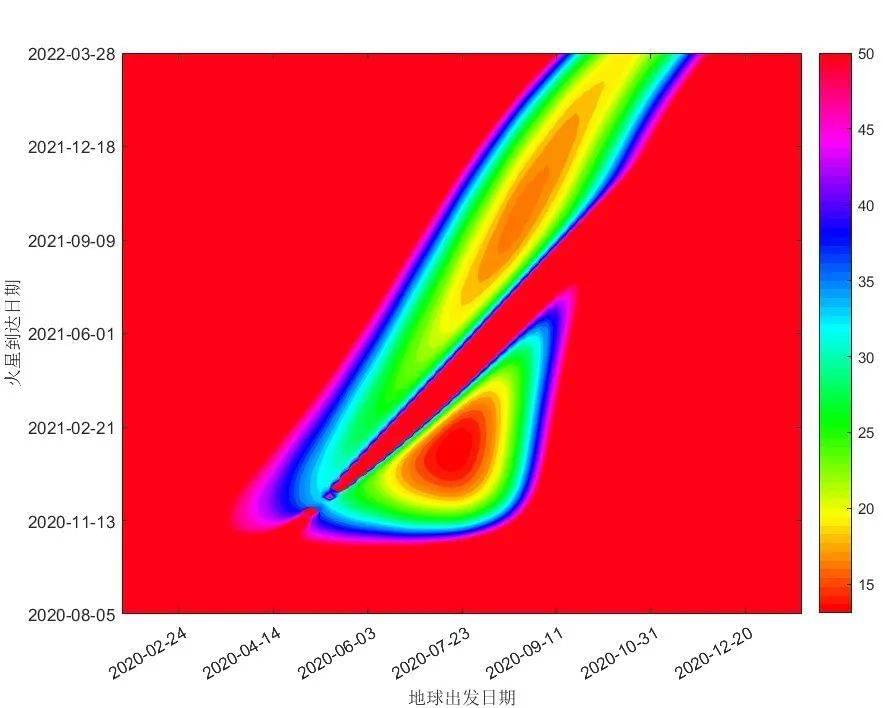
图 总需要速度增量和飞行时间
如果将等高线画为彩色,可以清晰地看到需要速度增量为双叶片特征形状,文献中称之为猪排图(哪儿像了?)。这里叶片以下的轨道称为第一类轨道(< 180°),而以上的轨道称为第二类轨道(> 180°)。
猪排图有助于早期任务设计人员选择发射日期、计算发射能量和速度增量预估值,以及可视化优化轨迹。发射周期的设计通过对一些参数(例如发射赤纬、到达日期、发射周期持续时间、进入速度、太阳角度)施加约束,同时使其他参数(例如发射能量、进入火星轨道速度增量)最小化。
当然,也可以将出发速度增量和到达速度增量拆开绘制,见下图所示。从文献中,喜欢采用C3和V∞表示,C3近似为地球变轨需要速度增量的平方,代表发射能量,V∞近似为火星到达需要速度增量。

图 出发和到达需要速度增量
从图中可以读出,2020年7月23日出发,离开地球轨道需要速度增量较小,2021年2月初到达火星,需要通过探测器减速约2.6km/s。
在文献3中,计算了不同年份登陆火星速度增量。
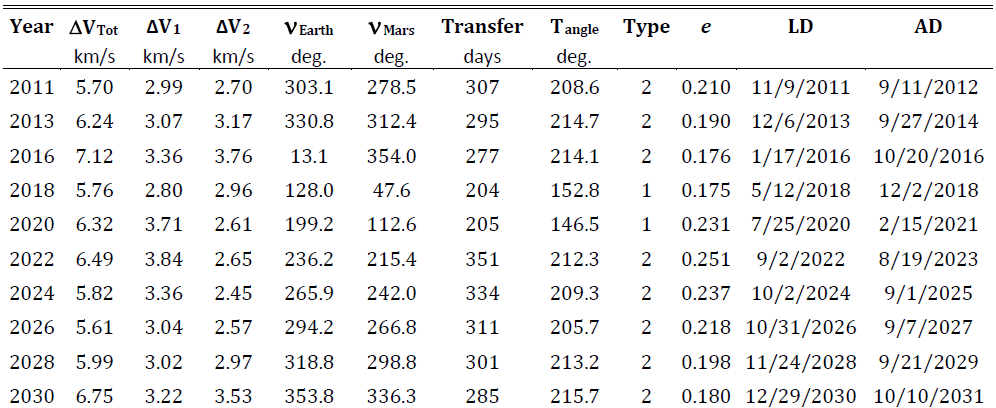
表 不同年份登陆火星速度增量计算表
这些不同中,到底是偏心率,还是轨道倾角等造成的呢?文献3中计算了5种不同工况:
工况1假设地球、火星为标准共面圆,此时最优转移轨道为霍曼轨道;
工况2考虑了地球和火星轨道偏心率(其它与工况1相同,下同),此时需要速度增量有所下降,但变轨时间增加;
工况3考虑了拱线变化,变轨时间进一步增加,且转移轨道多走了7°以追上火星;
工况4考虑了火星轨道倾角,此时需要一个额外速度增量进行转移轨道调整,但轨道周期等与标准霍曼变轨一致;
工况5综合了以上偏心率、拱线差异和倾角因素,得到一个最小速度增量5.6km/s,此时需要转移轨道需要比半圈多追25.3°才能赶上火星。对于近些年的探测任务,2026年对总速度增量需求较小,而2016年就不是一个好的探测年份。
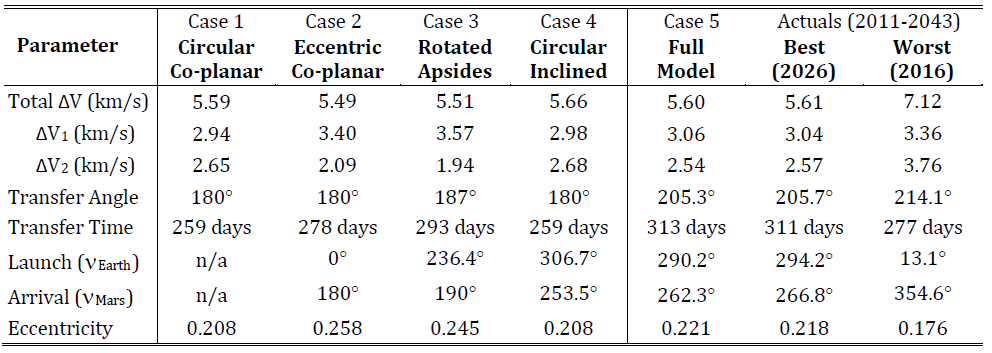
表 轨道偏心率、倾角等对转移影响
(类)霍曼转移轨道是最优的吗?
上述通过开普勒轨道模型或通过利用Lambert问题的解分析了火星转移轨道,在两种方法中,均只使用了两次脉冲推进,而两次脉冲推进是登火所需最小数量,其最优性也能得到证明。
如果使用更多次脉冲、甚至持续推力会不会更优呢?正如Edelbaum在1959年抛出的问题:How Many Impulses?以及,如果考虑推力、脉冲有限呢?
这个问题还没有终极答案,有理由相信,霍曼变轨多半不是最优的。理论上就有一种情况。
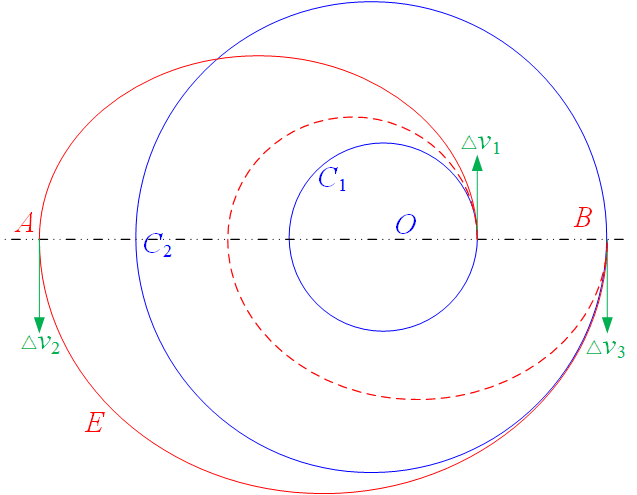
图 双椭圆转移示意图
如上图,对于共面圆轨道,为从轨道C1转移到C2,先通过∆v1加速到A点(可以比C2更远),然后在A点加速,使近地点抬升到与C2轨道相交的B点,之后减速。通过三次变轨,两次椭圆转移,到达新轨道。
令γ=r2/r1,α=ra/r1,可以得到无量纲需要速度增量(下式中加号代表A点在C2外,减号代表在内):
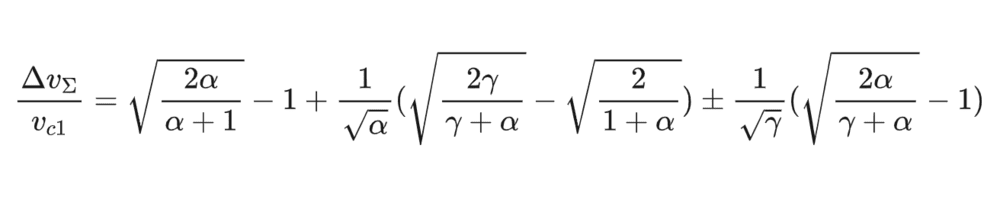
绘制不同中间椭圆半径对速度增量需求见下图。
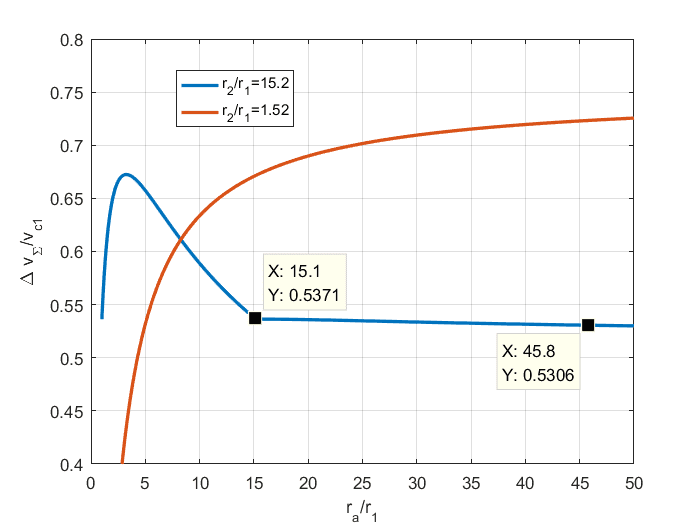
图 不同中间椭圆半径对速度增量需求
其中ra是可选择的,按优化条件可以求出最优的ra_opt及相应的速度增量。研究表明,如果ra_opt>r2,双椭圆转移更节省能量;如果ra_opt<r2,则宁愿选用霍曼转移。
双椭圆转移的极端情况是r2=∞,这称为无限双椭圆转移。
考虑霍曼转移无量纲需要速度增量:
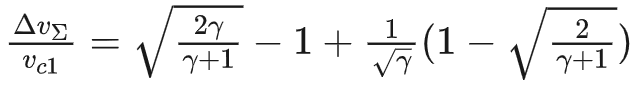
将无限双椭圆转移所需速度增量与霍曼转移做比较见下图所示。
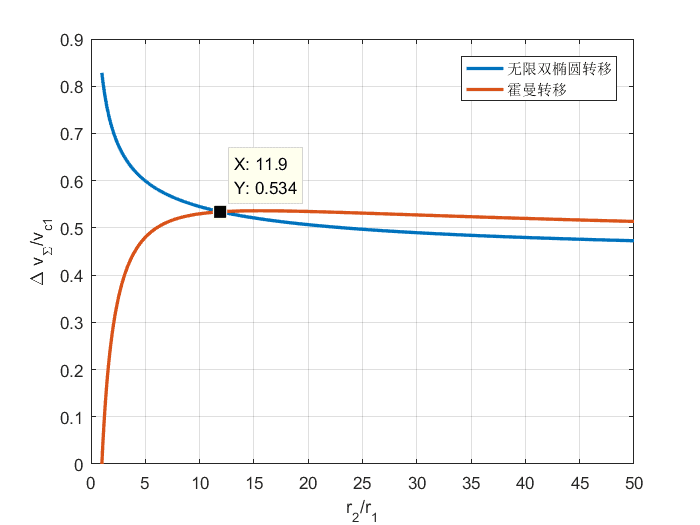
图 无限双椭圆转移和霍曼转移所需速度增量
两曲线交点对应r2/r1=11.94。当r2/r1<11.94时,霍曼转移较为有利。由于火星轨道与地球轨道的r2/r1=1.52,因此,还是采用霍曼变轨更节省能量。即使对于r2/r1较大情况,从图中看来,对速度增量需求减少8%,但这是靠大规模增加轨道转移时间获取的,所以实际意义并不大。
从这个角度,也许简单的霍曼变轨就足够优化了并且实用了吧。
参考文献:
1.Stinner A, Begoray J. Journey to Mars: thephysics of travelling to the red planet[J]. Physics Education, 2005, 40(1):35-45.
2.Prussing J E. Simple proof of the globaloptimality of the Hohmann transfer[J]. Journal of Guidance Control and Dynamics, 1992, 15(4): 1037-1038.
3.Woolley, Ryan C.; Whetsel, Charles W. On the nature of Earth-Mars porkchop plots. 23rd AAS/AIAA Spaceflight Mechanics Meeting.
4.Taheri E, Junkins J L. How Many Impulses Redux[J]. Journal of The Astronautical Sciences, 2019: 1-78.
5.肖亚伦. 航天器飞行动力学原理[M].宇航出版社, 1995.
6.https://au.mathworks.com/matlabcentral/fileexchange/39248-interplanetary-pork-chop-plots
7.罗治情. 地球--火星精确转移轨道设计算法研究[D]. 2012.
本文来自微信公众号:理念世界的影子(ID:spaceodyssey1968),作者:洞穴之外

