本文来自微信公众号:原理 (ID:principia1687),作者:原原,头图来自:Jagiellonian University
微分方程组是科学家用来预测物理世界行为的工具。这些方程将一个或多个未知函数及其导数联系起来。函数通常表示物理量,导数表示它们的变化率,微分方程定义了两者之间的关系。
微分方程分为两类,一类是只有单一变量的常微分方程,另一类是有多个变量的偏微分方程。这些方程非常常见,在工程、物理学、经济学、生物学等许多学科中,都发挥着重要作用。自牛顿和莱布尼茨时代开始,它们就一直是人们进行深入研究的来源。
然而,尽管几个世纪以来许多数学家作出了巨大的努力,但关于一些关键方程的解的存在性、唯一性、规律性和稳定性的基本问题仍未解决。
在帮助我们理解偏微分方程方面,没有其他仍然在世的数学家比路易斯·卡法雷利(Luis A. Caffarelli) 的贡献更大。他引入了巧妙的新技术,展示了出色的几何洞察力,并且带来了许多开创性的成果。
今天,挪威科学和文学学院决定将2023年阿贝尔奖授予卡法雷利,以表彰他“对非线性偏微分方程的正则性理论的开创性贡献,包括自由边界问题和蒙日-安培方程”。

改变方向
1948年,卡法雷利出生于阿根廷布宜诺斯艾利斯,在布宜诺斯艾利斯大学学习数学。1972年,他在导师卡利克斯托·卡尔德隆(Calixto Calderon)的指导下获得博士学位。
第二年,卡法雷利前往明尼苏达大学攻读博士后。在参加了数学家汉斯·路易(Hans Lewy)关于谐波分析的系列讲座后,他改变了研究方向。卡法雷利被路易提出的“障碍问题”吸引了。
障碍问题是非线性偏微分方程领域的一个经典问题,它探讨的是当一个弹性膜被推向一个刚性障碍物时,例如当一个气球被压在墙上时,平衡位置是什么。
很快,他就开始在这个课题上取得惊人的进展,并开始探索更广泛的“自由边界”问题。之所以被称为“自由边界”,是因为这类问题所讨论的边界在一开始是未知的。比如在刚才提到的气球例子中,自由边界是气球会在哪里碰到墙壁。还有一些其他的自由边界问题的例子,比如冰融化成水,这里的自由边界是冰和水之间的交界。
1976年,他发表了六篇论文,并于1977年首次在著名的《数学学报》上发表论文:《高维自由边界的规律性》。
唐人街散步
1980年,卡法雷利来到纽约大学专门研究应用数学的科朗研究所。有一天,在与罗伯特·科恩(Robert Kohn)和路易斯·尼伦伯格(Louis Nirenberg)在唐人街的一次散步中,他们决定共同撰写一篇关于纳维-斯托克斯方程的论文,这是一组模拟流体动力学的偏微分方程。
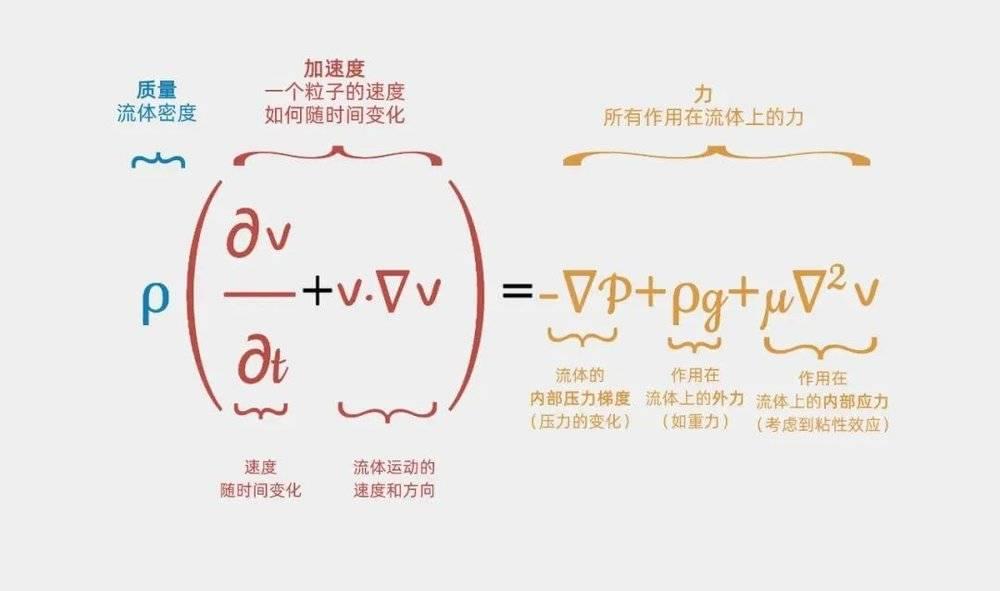
这次合作的成果是1982年的论文《纳维-斯托克斯方程的合适弱解的部分规律性》,这是一篇具有里程碑意义的论文,后来获得了美国数学学会2014年斯蒂尔开创性研究贡献奖。
当尼伦伯格后来被问及如何评价卡法雷利作为一位数学家时,他回答说:“非凡的直觉,很了不起……我很难跟上他的步伐。他总能神奇地立即看到其他人看不到的。”
到80年代初,卡法雷利在数学界已经有了很高的知名度,并获得了众多著名的奖项,比如1982年的圭多·史坦穆奇亚奖,1984年的博谢奖。此外,他还是1983年在华沙举行的国际数学家大会上的发言人。
1983年至1986年期间,卡法雷利在芝加哥大学担任教授,之后他在普林斯顿高等研究院工作了十年。在此期间,他的另一个主要的工作重点是蒙日-安培方程,这是另一个著名的非线性偏微分方程。他发展了现在所谓的“卡法雷利正则理论”,该理论在其他领域有重要的应用,例如最优运输理论。
培养学生
卡法雷利怀念与研究生一起工作的日子,他于1994年回到科朗研究所。1997年以后,他一直在德克萨斯大学奥斯汀分校担任数学方面的西德-理查德森主席。 在那里,他除了完成其他日常工作外,还在均质化理论方面取得了令人兴奋的进展,这是一个偏微分方程研究领域,研究不同尺度的物理性质。
卡法雷利不仅在工作的深度方面非常出色,而且非常高产。年过74岁的卡法雷利已发表的论文多达320篇,并且每年还在继续发表。他在科学界备受爱戴,曾与130多人共同撰写论文,最常与他合作的是阿夫纳·弗里德曼(Avner Friedman)。卡法雷利的论文有19000次引用,这个数字证明了他在领域内的影响力。他曾为30多名博士生提供指导,2018年,他的博士后阿莱西奥·菲加利(Alessio Figalli)获得了菲尔茨奖。
卡法雷利获得的其他奖项包括2005年罗夫·肖克奖、美国数学学会2009年斯蒂尔终身成就奖、2012年沃尔夫奖、2013年所罗门·莱夫谢茨奖和2018年邵逸夫奖。
阿贝尔委员会主席Helge Holden说:“将出色的几何洞察力与巧妙的分析工具和方法相结合,他已经并将继续对该领域产生巨大影响。”
参考来源:
https://abelprize.no/
本文来自微信公众号:原理 (ID:principia1687),作者:原原

