本文来自微信公众号:未尽研究 (ID:Weijin_Research),作者:Nicholas Bloom、Charles I. Jones、John Van Reenen和Michael Webb,原文标题:《创新,越来越必要,也越来越难》,头图来自:《流浪地球2》剧照
无论是新训练出一个人工智能算法大模型,研发一种创新药,还是让核聚变产生的能量能烧开一壶水,所投入的资金越来越多,从几亿美元到几十亿甚至上百亿美元;所耗费的时间越来越长,从几个月几年,到十年和数十年。
而一个国家的经济发展,在追赶发达国家、跟随创新技术到一定水平后,如中国发展为高收入经济,为了维持经济的持续增长,必须在技术创新方面投入越来越多。从美国等创新领先国家的经验来看,一方面是如摩尔定律等能维持近60年指数增长,另一方面是为了维持这一增长所耗费的资金量也越来越大。
人类创新之路,越走越难?还是创新急需新的范式革命,进入下一条创新增长曲线?下面这篇关于美国创新效率下降的研究表明,不断增加创新的投入,是为了维持经济增长不得不做出的努力。

在许多模型中,“长期增长”是两个术语的产物:研究人员的有效数量和研究人员的研究生产率。我们研究了来自不同行业不同产品和不同公司,结果显示,研究工作量在大幅上升,而研究生产率却在急剧下降。更普遍地说,无论我们将目光投向哪个领域,我们都发现,创新——以及它们所可能蕴含的指数级增长,正变得越来越难。
经济的增长来自于人们所创造的想法。如将长期增长率视作会计问题,我们可以将其分解为两个项的乘积:研究者的有效数量和他们的研究生产率。我们发现,在许多背景下和在各种不同行业中,研究努力正在大幅上升,而研究生产率正在急剧下降。而稳定增长则是这两种趋势相互抵消的结果。

可以佐证这一发现的最好例子是摩尔定律——这是近几十年来经济增长的关键驱动因素之一。摩尔定律由英特尔创始人之一戈登·摩尔提出,其核心内容为:集成电路上可以容纳的晶体管数目在大约每经过18个月到24个月便会增加一倍。
这种翻番相当于每年35%的指数增长率,这一增长率在近半个世纪以来一直非常稳定。而这种增长是通过吸引越来越多的研究人员投身其中从而推动摩尔定律向前发展而实现的。现如今,将芯片密度翻倍所需的研究人员数量是20世纪70年代早期的18倍多。在这种情况下,研究效率正在以每年7%的速度急剧下降。
除摩尔定律之外,我们还研究了农业生产力(玉米、大豆、棉花和小麦)和医疗创新。我们发现,对种子产量的研究生产率以每年约5%的速度下降。在研究与癌症和心脏相关疾病的死亡率改善时,我们发现了类似的降速。
最后,我们研究了两个公司层面的数据,Compustat数据库(译注:Computat是一个全面的财务数据库,收录公司的营运及财务状况资料。数据库涵盖130多个国家,超过92000上市/已退市公司,超过113343只证券,占全球市值97%以上;财务数据回溯到1950年。)和美国制造业普查数据库。我们发现,Compustat的研究生产率每年下降约10%,美国制造业普查数据库则每年下降8%。
一、如何衡量创新?
注:这一部分的模型和数学公式部分,请见文章结尾之后的说明。
图1研究了美国增长与研究的数据。我们可以看到,自1930年以来,研究人员有效数量有了大幅增加。
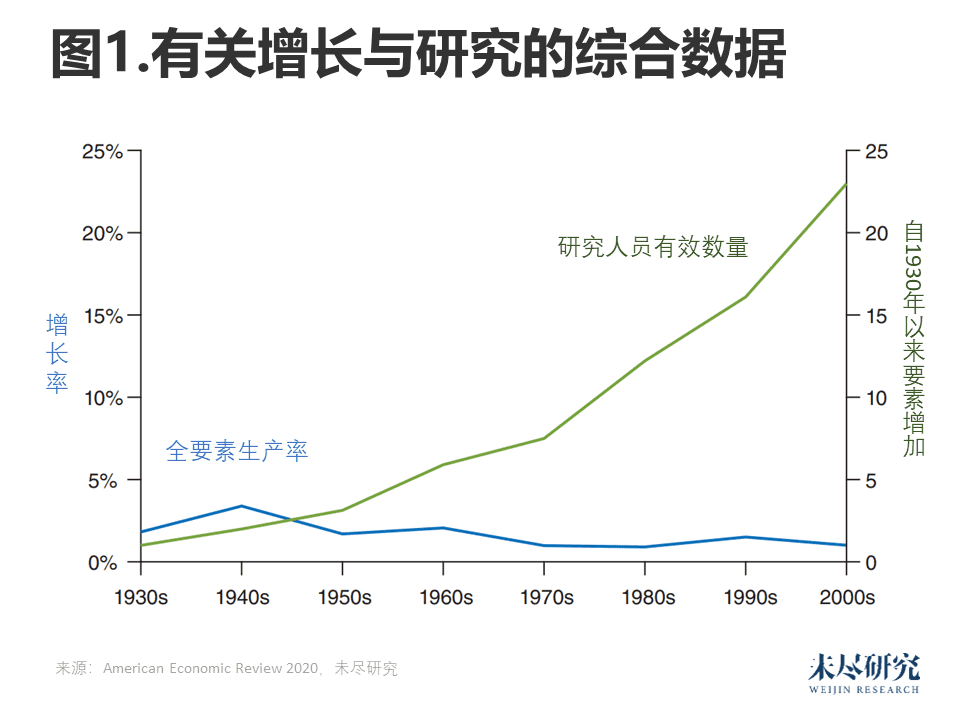
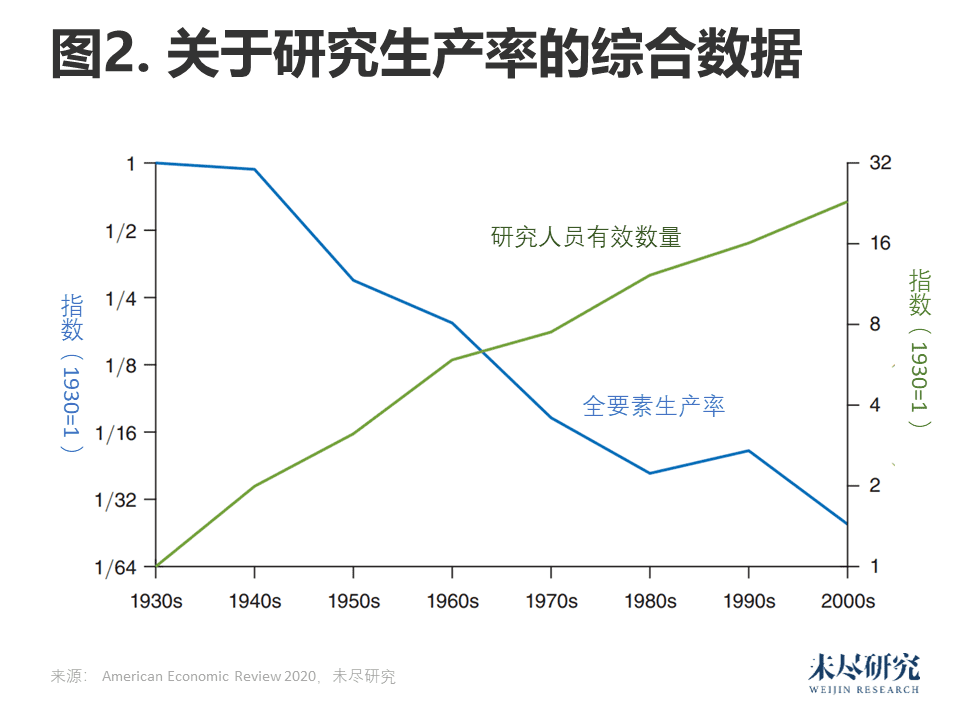
图2显示了以十年为一个周期计算的研究生产率和研究工作情况。自20世纪30年代以来,研究成果增加了23倍,平均每年增长4.3%。研究生产率下降幅度更大,下降了41倍,平均每年增长−5.1%。从结构上看,下降23倍主要是由于研究工作的增加,极少一部分是由于众所周知的TFP增长率的下降。
二、摩尔定律
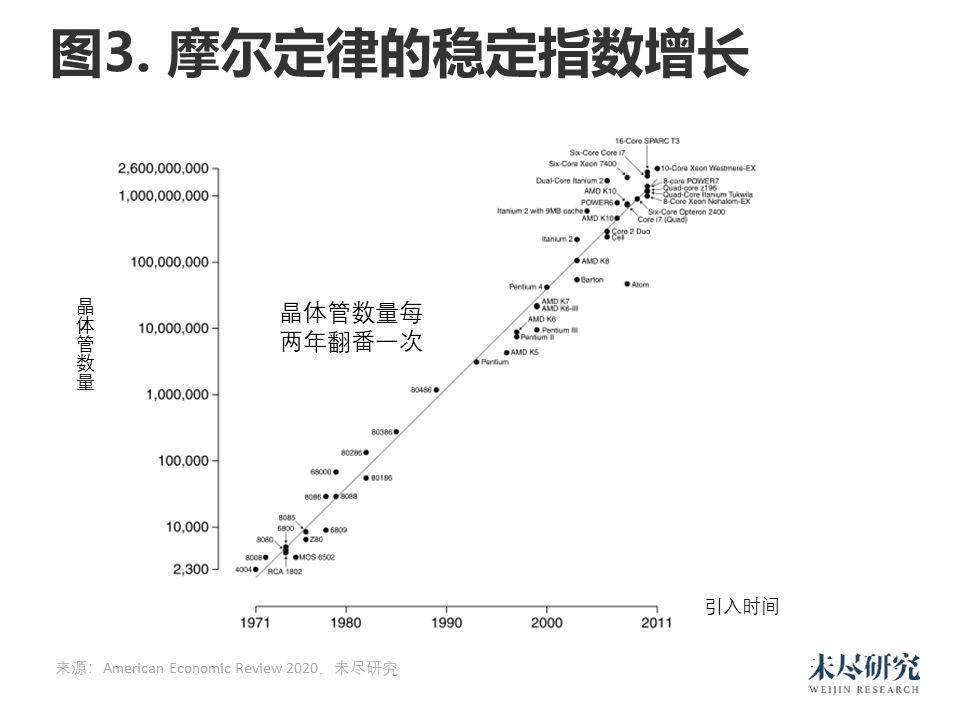
摩尔定律是过去半个世纪经济增长的关键驱动力之一。摩尔定律指的是,作为计算机中央处理单元的集成电路上的晶体管数量大约每两年翻一番。图3显示了自1971年起的这种规律性,及其所蕴含的巨大增长率。
如图4所示,一个惊人的事实是,自1971年以来,研究工作增加了18倍。这种增长发生在芯片密度的增长率相对稳定的时候:摩尔定律所带来的持续性指数增长仅通过资源的大量投入即可实现。
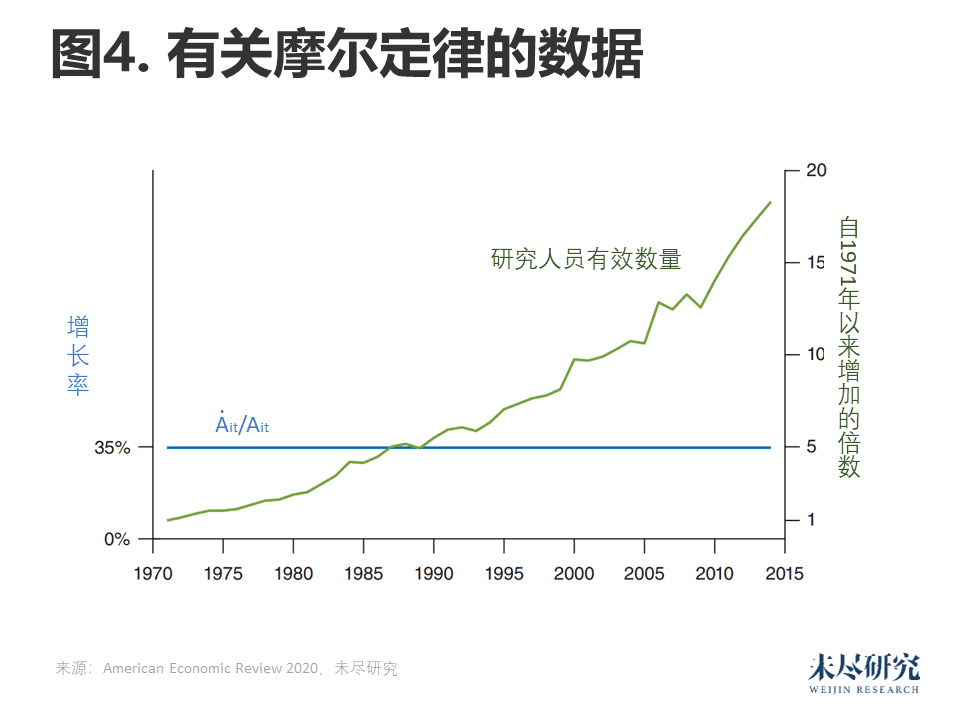
假设摩尔定律的增长率恒定不变,这意味着研究生产率下降了18倍,平均每年下降6.8%。如果持续研究生产率的零假设是正确的,那么摩尔定律背后的增长率也应该增加了18倍。相反,它却非常稳定。换句话说,由于研究生产率的下降,现如今要支撑起摩尔定律的指数增长比1971年时困难18倍。
三、农业
我们研究的下一个对象是农业。图5展示了整个农业部门的研究生产率情况。在1970年到2007年间,农业领域的TFP增长率略有下降,而有效研究增长了大约两倍。因此,在此期间,研究生产率下降了近四倍,平均每年下降3.7%。
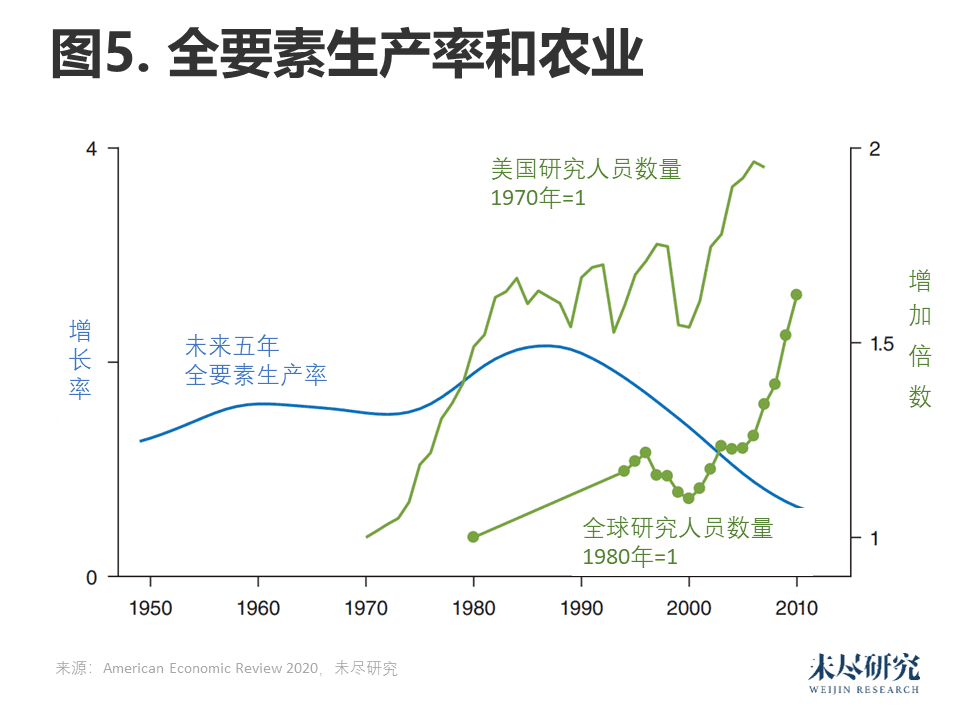
我们着重研究了各种农业作物的生产率。对于玉米、大豆、棉花和小麦,我们都获得了关于作物产量和旨在提高作物产量的研发支出的数据。自1960年以来,这四种作物的产量平均年增长率约为1.5%。
图6显示了5年平均年化产量增长率(经过调整以消除主要由天气造成的冲击)。图中的绿线显示了衡量每种作物的“有效”数量的指标,即公共和私人研发支出之和与高技能工人工资之间的差距。
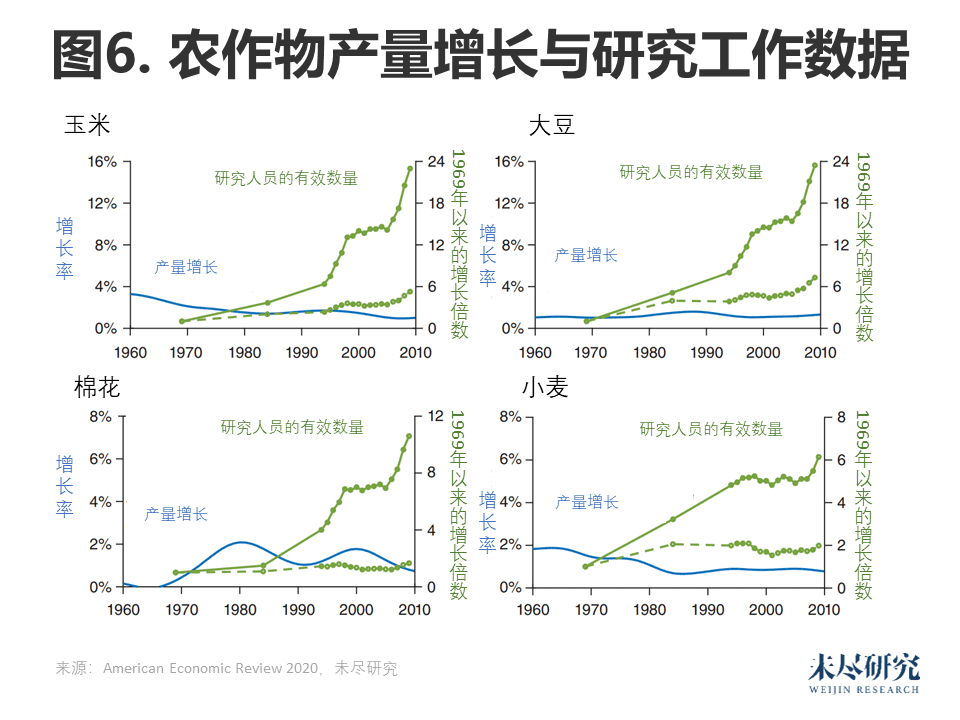
从图6中可以看出,农业产量的研究生产率急剧下降:产量增长相对稳定,甚至在下降,而推动产量增长的有效研究却大幅上升。研究生产率就是平均产量增长除以研究人员数量得出的结果。
四、医学研究
我们的第三个案例研究考察了医学研究的生产率。医疗支出约占美国GDP的18%,健康生活是人们购买的最重要的商品之一。
我们首先从预期寿命开始。图7显示了美国人出生时和65岁时的预期寿命。
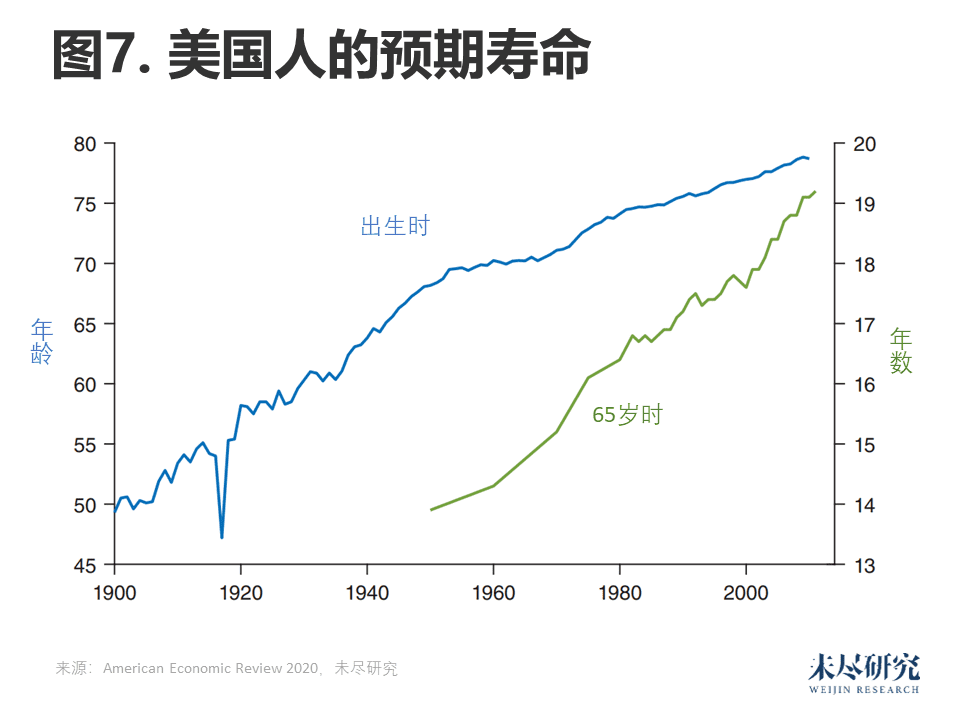
这张图表说明了一个重要的观点,即预期寿命是少数几种不呈指数级增长的经济产品之一。相反,算术增长是更为合适的描述方式。自1950年以来,美国人出生时的预期寿命以每10年1.8岁的相对稳定的速度增长,而65岁时的预期寿命以每10年0.9岁的速度增长。
预期寿命的线性增长似乎与经济增长相一致。预期寿命的稳定线性增长,而不是指数增长,似乎是常态。因此,我们在此使用“所挽救的生命年数”,即预期寿命的变化,而不是其增长率,来衡量研究工作的产出。
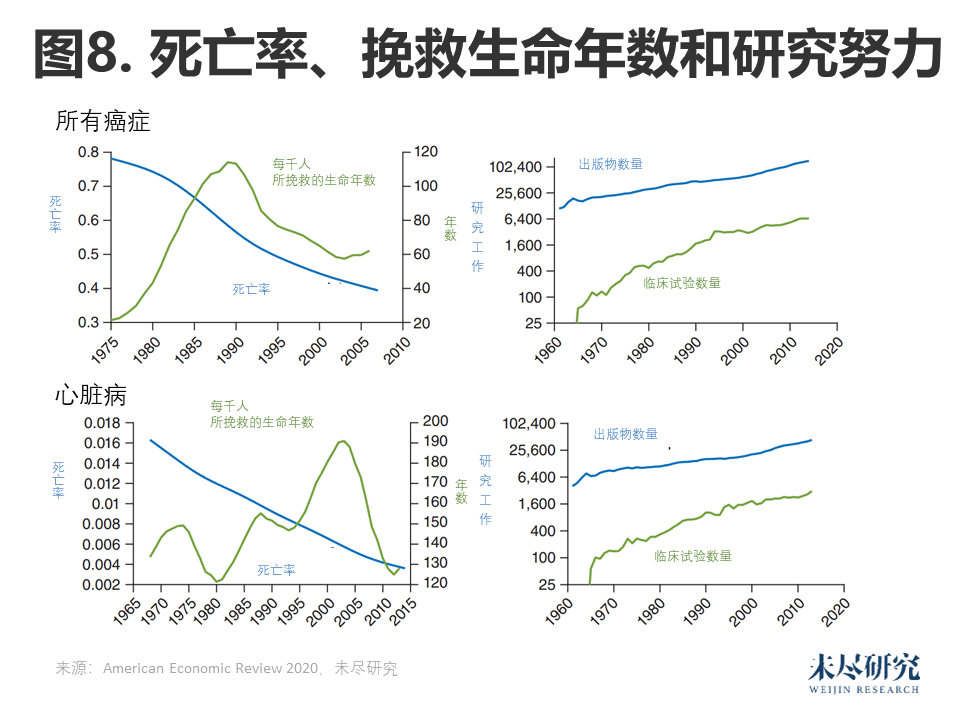
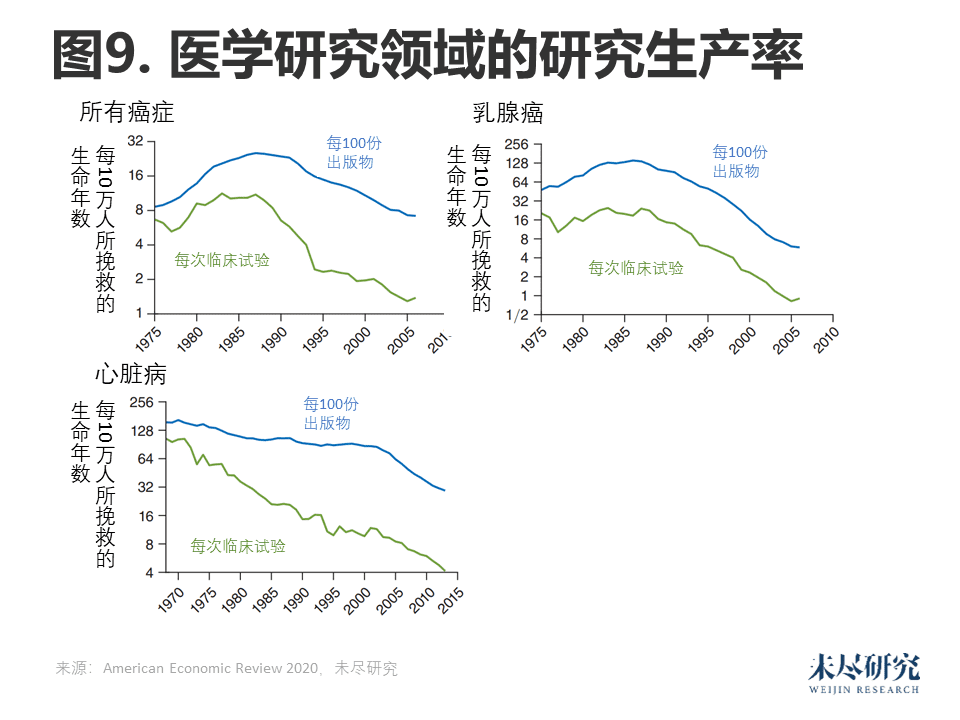
我们对医学研究生产率的定义是所挽救的生命年数与出版物数量之比。从1975年到2006年,所有出版物对所有癌症的研究效率下降了1.2倍,临床试验则下降了4.8倍。乳腺癌和心脏病等特定疾病的下降幅度甚至更大。
五、在企业级数据中的研究工作效率
我们研究了两组公司层级数据。第一组是美国上市公司的计算数据(2016)数据。第二组是来自制造业普查的管理数据。
在我们所有的样本中,研究生产率以每年约9%的速度下降,每十年累计下降2.5倍。按照这个速度,在30年的时间内,研究生产率下降了大约15倍;换句话说,现在需要比30年前多15倍的研究人员,才能产生同样的公司收入增长率。
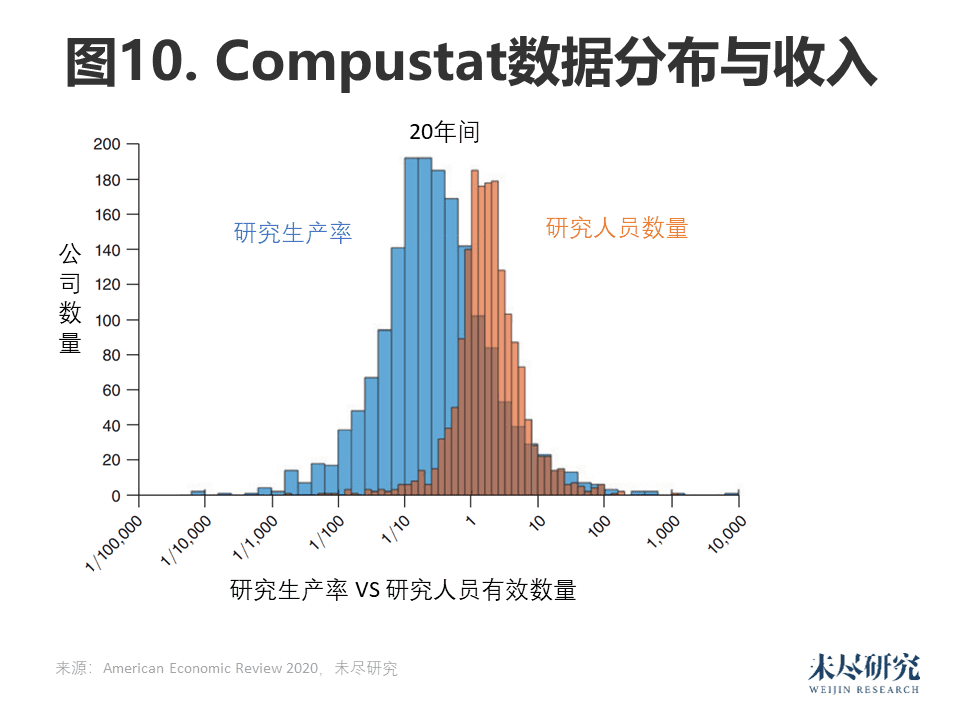
图10通过显示了不同公司的有效研究和研究生产率的因素变化的分布。在这个图中,我们关注的是20年来公司的销售收入结果,但其他产出指标和其他时间范围的结果是相似的。
六、思考及结论
如下表所示,在我们看到的几乎每个地方,研究生产率都在以可观的速度下降。
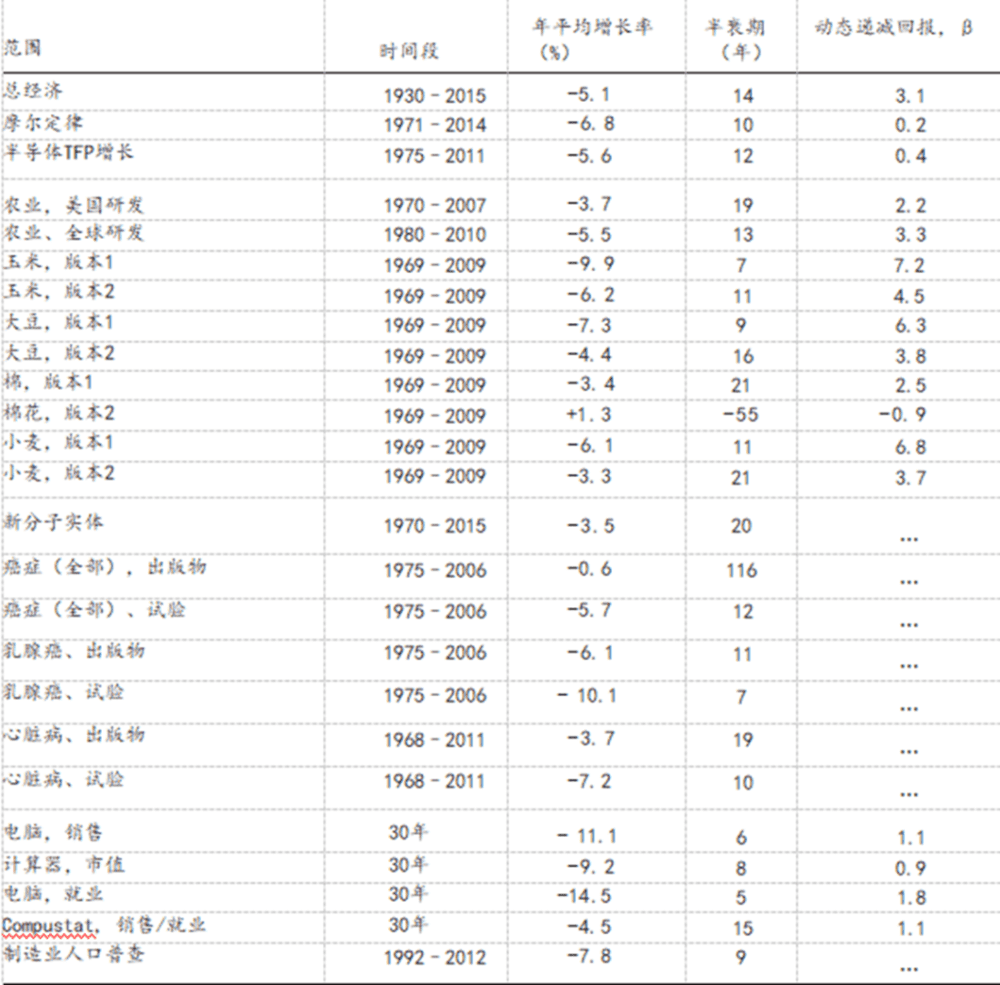
综上所述,我们的发现是,无论我们将目光投向哪里,研究效率都在急剧下降。以美国为例,研究生产率每13年就会下降一半:创新越来越难找到。换句话说,为了维持人均GDP的持续增长,美国必须每13年将研究成果增加一倍,以抵消在寻找创新的困难。
我们必须跑得越来越快,以保持恒定的指数增长。如果研究投入的增长率放缓,这可能会导致经济增长本身放缓。
附:如何衡量创新
许多增长模型的核心方程是一个采用一种特殊形式的创意/生产函数:
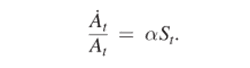
方程(1)
在这个方程中, 指经济中的全要素生产率(TFP)。变量St指某种形式的研究输入,比如研究人员的数量。该方程式表明,通过创新来实现的经济增长率,与研究人员的数量是成正比的。
有关A˙t/At和创新的关系,一个绕不开的问题是,创新很难被衡量。即便是如“创新的单位是什么?”这样简单的问题都十分令人困扰。我们大量查阅相关文献后认为,创新的单位应有助于体现A中由持续不断的新想法而产生的持续指数增长。比方说,每一个新创意平均为收入带来了多少百分比的增长,而不是具体带来了多少金额的增长。这个定义意味着,方程(1)的左边等同于创新的流动。
现在,我们可以将创新生产函数的生产力定义为创新输出与产生这些输出的输入之比:
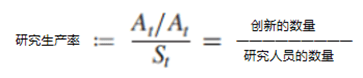
本文检验的零假设来自于(1)中假设的关系。将这个方程代入研究生产率的定义中,我们可以看到(1)意味着研究生产率等于α,即研究生产率随时间的变化是恒定的。在这个零值下,恒定数量的研究人员可以产生恒定的指数增长。
从公式(1)中可以很容易地推导出一个结论:在研究生产率的持续稳定的情况下,永久增加研究人员数量及研究补贴将永久地提高经济的增长率。换句话说,“持续的研究生产率”和持续的研究补贴将产生“永久增长效应”。
本文来自微信公众号:未尽研究 (ID:Weijin_Research),作者:Nicholas Bloom(斯坦福大学经济系)、Charles I. Jones(斯坦福大学商学院)、John Van Reenen(MIT经济系)和Michael Webb(斯坦福大学经济系 )

