本文来自微信公众号:原理(ID:principia1687),作者:小雨,题图来自:《美国队长3》
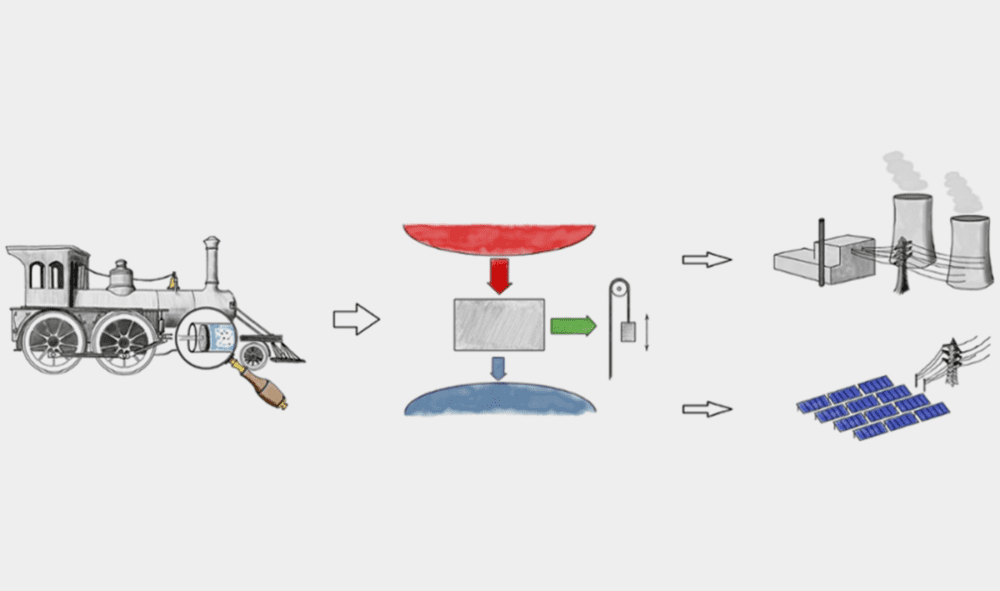
卡诺循环式由法国物理学先驱尼古拉·卡诺于1824年提出并设计的。这一设计为将热量转化为功的效率,以及(通过在不同温度和压力下循环一个封闭系统从而)将功转化为热量的效率提供了上限。可以说,对这一过程的理解,支撑了整个西方在工业革命期间的经济发展。
量子熵
随着量子信息科学的发展,一种奇异的现象——量子纠缠,开始在量子通信、计算和密码学等任务中扮演重要角色。当两个微观系统纠缠在一起时,它们的性质是相互关联的,而这种关联性与两者之间的物理距离无关。
有趣的是,尽管量子系统大多是在微观体系中研究的,但量子纠缠与热力学有许多深刻的相似之处。在量子纠缠理论和热力学之间,已经存在许多卓有成效的类比。这促使人们开始探讨,纠缠理论是否可以像热力学定律那样存在公理化的描述,以及是否可能存在类似于熵的函数来度量纠缠。
一些科学家家提出了“纠缠熵”的概念。在过去的研究中,科学家已经证明对于那些能与周围环境完全隔离的理想量子系统来说,纠缠熵可以精确地模拟热力学熵的作用。
在考虑量子纠缠时,一个基本问题是,纠缠是否总是能被可逆操纵,就像卡诺循环一样。而且关键是,这种可逆性要能够保持,至少在理论上,即使对于那些没有与环境完全隔离的量子系统,也是如此。
是否可能建立一个“纠缠第二定律”,成了一个长期悬而未决的问题。
一种特殊状态的创建
为了解决这个问题,一个国际物理学家团队在近期的《自然·物理》杂志上发表了一项新的研究,他们的最新结果表明,想要建立一个与热力学第二定律直接对应的“纠缠第二定律”,是不可能做到的。
这项研究是通过证明纠缠理论的不可逆来实现的。研究依赖于对一种特殊的量子态的构建,这是一种在此前未知的量子态。使用纯纠缠来创建这种特殊量子态会“代价高昂”,因为它的创建总伴随纠缠的损失。
换句话说,投入的纠缠无法被完全恢复。因此,想要将这种状态变换成另一种状态,再从另一种状态变换回来,是根本不可能的。
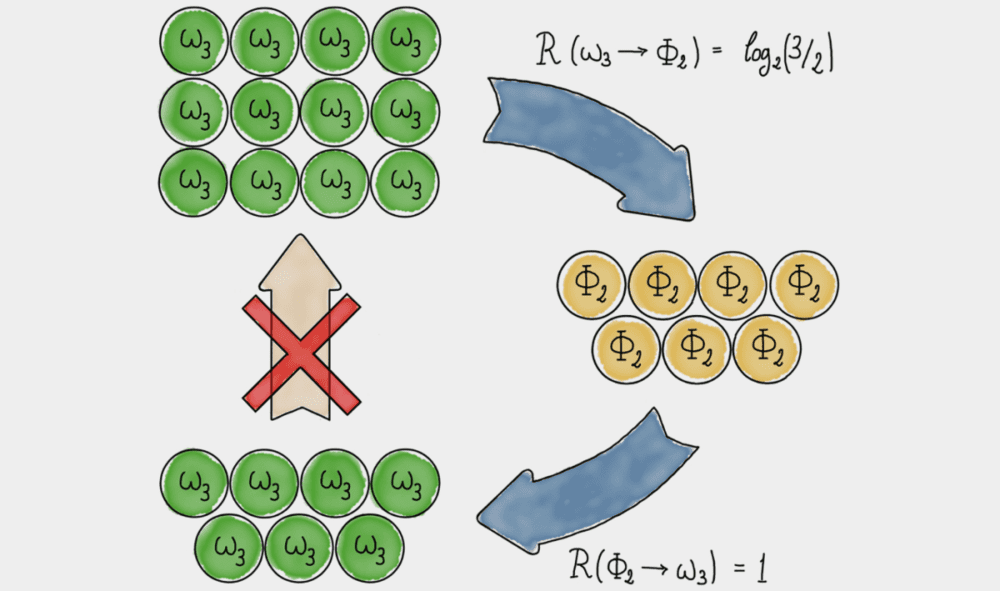
没有第二纠缠定律
在这项新研究中,研究人员所使用的这种方法并没有预先假设会使用哪种确切的变换,因此它排除了所有可能情况下的纠缠可逆性,证明了这种不可逆性适用于所有变换。
除此之外,他们还进一步得出结论认为,不存在一个类似“纠缠熵”这样的单一变量,可以揭示关于纠缠系统所允许的变换的所有信息。这意味着,量子纠缠变换和热力学过程之间存在根本的区别,它们由完全不同且不相容的一系列定律所支配的。
新的研究界终结了所有关于建立纠缠第二定律的希望。它意味着,过去物理学家对量子纠缠与热力学进行的比较,是有其局限性的,与经典热力学定律相比,量子纠缠的复杂性可能要大得多。
不过,这项研究的作者表示,我们并不需要对这样的结论感到沮丧,因为它或许能让科学家通过利用量子纠缠,来实现在其他情况下完全不可想象的成就。而且它也让物理学家深刻地意识到,量子纠缠隐藏着一个比我们以为的还要丰富、繁杂的世界。
参考来源:
https://www.uva.nl/en/shared-content/subsites/institute-of-physics/en/news/2023/01/no-second-law-of-entanglement-after-all.html
https://www.nature.com/articles/s41567-022-01873-9
本文来自微信公众号:原理(ID:principia1687),作者:小雨

