破解黎曼猜想的新思路

本文来自微信公众号：原理（ID：principia1687），作者：小雨，头图来自：unsplash

黎曼ζ函数（ζ，读作zeta）是一个看似简单且普遍存在的函数，自19世纪以来，这个函数一直困扰着数学家，与之相关的黎曼猜想也成了位列千禧年大奖难题的未解之谜之一。

最近，在《物理评论快报》刊登的一篇论文中，物理学家Grant Remmen阐明了他运用物理学的思维，发展出了一种可以探索ζ函数的许多古怪之处的方法。在这种新的方法中，他将黎曼ζ函数的许多重要性质都转化为量子场论。这意味着现在我们可以利用物理领域的工具来研究这个神秘而又奇怪的函数，甚至可能带领我们更进一步地接近黎曼猜想的证明。

黎曼猜想  

在数论领域，ζ函数是一个随处可见的数学函数，它以一种无穷的调和级数的形式存在。

ζ(s)函数，s代表函数中的指数变量，ζ(2)指的就是级数的平方和，ζ(4)是级数的四次方和，以此类推。

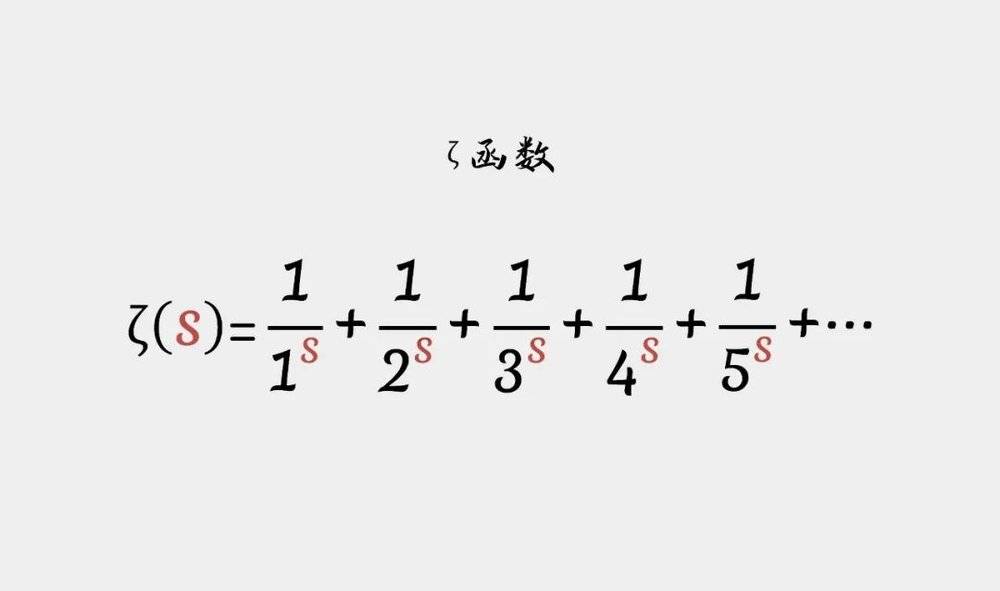
当s>1时，ζ函数是收敛的，它会收敛到某个有限数值。

1859年，数学家黎曼（Bernhard Riemann）开始思考：如果代入ζ函数中的s是复数，会发生什么？他将ζ函数扩展到了复平面，发现ζ函数只有在s的实部大于1时才是收敛的。

为了将ζ函数扩展到复平面的其余部分，黎曼使用了复分析中的一种被称为解析延拓的技术。解析延拓的关键在于，实际上要有两个函数在同时运作，一个是原始的ζ函数，它的运作范围有限，即仅限于s的实部大于1的范围；另一个是一个全新的、定义域被扩展了的函数——黎曼ζ函数：当ζ函数收敛时，黎曼ζ函数的值等同于原始的ζ函数；当s的实部小于1时，黎曼ζ函数的值就等于由s处的级数定义的函数的解析延拓。（注：ζ函数无法被扩展到整个复平面，它在s的实部等于1时没有意义。）

在复平面上被扩展了定义域的ζ函数，函数可以穿过原点。| 图片素材来源：Grant Remmen, Harrison Tasoff

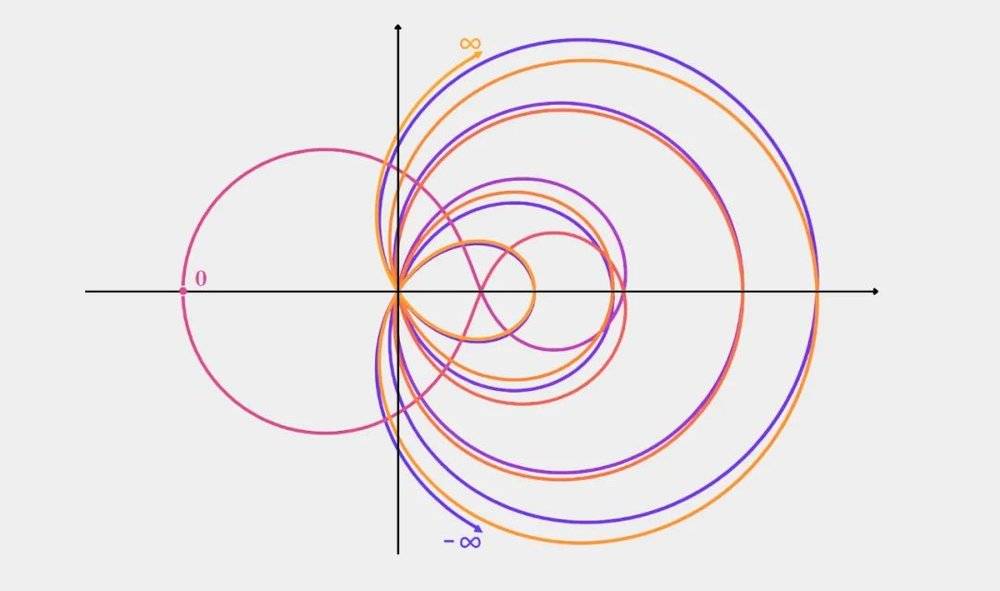
通过扩展函数的域，黎曼发现在新的域里，函数可以穿过原点。这意味着当对函数输入一些特定的值时，函数值为0，这些值被称为ζ零点。比如所有的负偶数都是ζ零点。

不过，这些所谓的“平凡零点”并不是数学家所不感兴趣的，黎曼所在意的是那些被称为“非平凡零点”的输入，因为他注意到，所有的非平凡零点似乎都处于一条直线上。

函数ζ黎曼认为所有非平凡零点都位于一条直线上。| 图片参考来源：新原理研究所

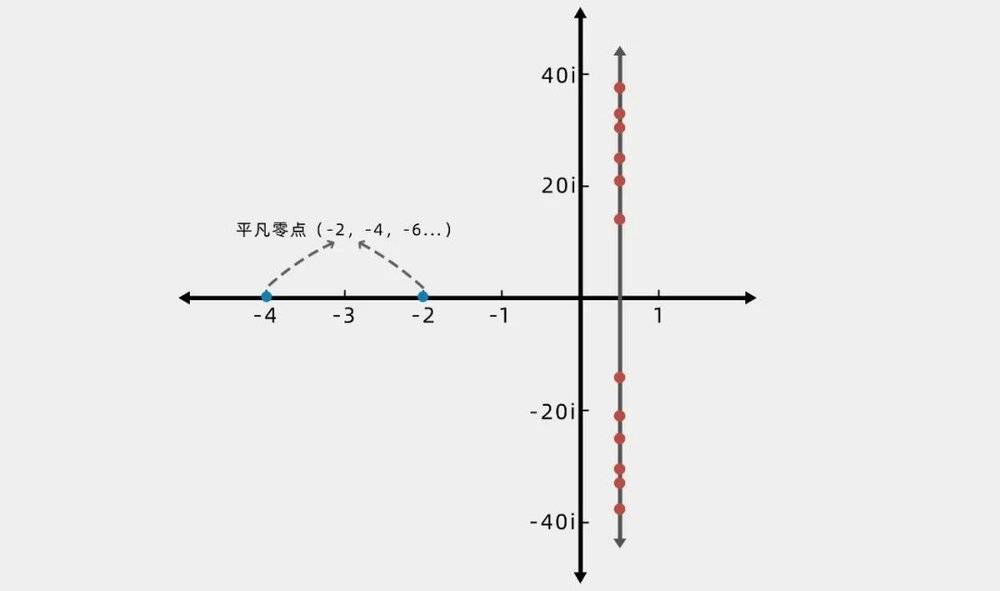
于是，黎曼提出假设，认为这种模式适用于所有的非平凡零点，具体来说，黎曼猜想说的是：所有非平凡零点都位于一条直线上，也就是在复平面上s的实部等于1/2的地方。

现在，这一猜想已经在大量例子中都得到了证实，但这仍不足以证明猜想的成立。

量子场论引发的思考  

Remmen的日常研究工作并不专注于破解数学中的大问题，而是试图解决与量子引力、弦理论和黑洞有关的重大问题。量子场论是他的专长之一，该理论将狭义相对论和量子力学结合了起来描述以光速或接近光速运动的粒子的行为。

Remmen意识到，在量子场论中，一个被称为散射振幅的概念与黎曼ζ函数有许多相同的特征。散射振幅编码了量子力学中的粒子相互作用的概率。通常，它适用于动量是复数的情况，它在复平面上有着很好的性质。在复平面上，它们围绕着的每一点都是解析的（即可以表示为级数），除了一组都在一条直线上的极点（不能用级数表示的点）之外，这与黎曼ζ函数的非平凡零点似乎也都在一条直线上相似。

图中所示的是Remmen的散射振幅，它能将黎曼ζ函数转化为量子场论的语言。 | 图片来源：Grant Remmen

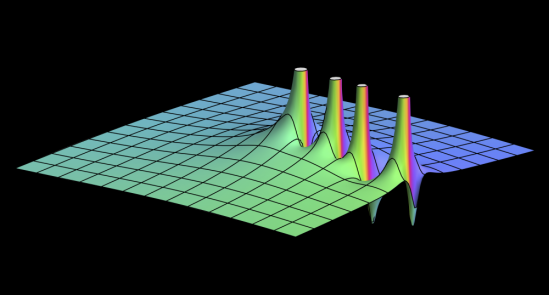
因此，Remmen想知道，在这种表面上的相似性背后，是否有存在什么真实的含义。

ζ函数的量子场论版  

Remmen想要发展出一种方法，可以将量子系统中的散射振幅映射到黎曼ζ函数的数学特征上。他考虑的是一个量子粒子碰撞系统，用涵盖了粒子在散射过程中的能量、动量和轨迹的变量来描述粒子。利用这些变量，他在ζ函数的基础上，构建了一个具有散射振幅的所有特征的数学函数。

Remmen的散射振幅描述了两个无质量粒子通过交换无穷个大质量粒子进行相互作用。在他的函数中，极点对应于每个中间粒子的质量，无穷多个这样的极点对应于黎曼ζ函数中的非平凡零点。

黎曼猜想假设ζ函数的非平凡零点都具有等于1/2的实部，把这个转化到Remmen的模型中，意味着所有振幅的极点都是实数。也就是说如果有人能证明Remmen的函数描述了这样一个一致的量子场论，即质量是实数而非虚数，那么他就证明了黎曼猜想。

ζ函数的量子版  

Remmen的函数将黎曼猜想带入了科学和数学的另一个领域，为数学家提供了强大的工具。它表明不仅黎曼猜想中存在这种对应关系，而且黎曼ζ函数中还有许多其他属性也与散射振幅的物理性质相对应。例如，Remmen已经用物理学的方法发现了一些与ζ函数相关的数学恒等式。

现在，Remmen希望利用物理学中的散射振幅可以更多地了解ζ函数。这种方法为或许能够为证明这个伟大的猜想开辟一条新的道路。而且，在证明这个振幅的确来自于一个合理的量子场理论时所能带来的新思路，也将为我们提供充分理解ζ函数所需要的工具。

现在，Remmen构建的是相互作用中最主要的组成部分，还有无穷多个包含了那些小的相互作用的部分，那些“环级振幅”将会是未来研究的主题。

参考来源：

https://www.news.ucsb.edu/2022/020520/quantum-zeta-epiphany

https://physics.aps.org/articles/v14/s157

本文来自微信公众号：原理（ID：principia1687），作者：小雨