生物学中的拓扑

本文来自微信公众号：原理（ID：principia1687），作者：小雨，题图来自：Unsplash

一

在什么样的情况下，我们能够说一个系统的某个性质是稳健的（robust）？一个性质如果是稳健的，则意味着即使系统受到了外部扰动的影响，且无论这种影响有多么强或多么随机，这种性质仍然能保持不变。

在数学中，物体在形变方面的稳健性被称为拓扑。例如字母s、S、L的形状在拓扑学中就属于同一范畴，具有相同的拓扑，可以通过拉伸或弯曲它们的形状而相互转换；字母o、O、D属于另一范畴，而S和O之间不能进行这种转换，除非将O切开，或将S的两端粘在一起。也就是说，拓扑学描述的是一个物体除非被撕裂，不然无论被如何拉伸、扭曲或者畸变，都会维持不变的特性。

在过去的几十年里，物理学家发现量子系统的某些性质只取决于系统的某些基本特征的拓扑，最著名的例子之一就是量子霍尔效应。这种现象发生在当二维的导电材料遇到垂直于它的磁场时，在这种情况下，材料中的电子会在被称为回旋轨道的小圆圈中移动，在材料的大部分区域不会产生任何净电流，然而在材料的边缘，电子会在完成一个回旋之前反弹，然后朝着相反的方向移动，导致电子沿着边缘产生净流动。

这种边缘电流是独立于边缘的形状的，即使边缘出现强烈的形变，这种电流也能持续存在，这凸显了量子霍尔效应的稳健性。这也是为何拓扑学会被用来描述量子霍尔效应中的导电现象。

 图中显示的是一个在经历边缘循环的生物化学系统，这是一个由6个亚基（绿色方片和紫色圆形）组成的蛋白质复合物，这些亚基可以改变形状或与另一个分子（黄色圆形）结合。当其中所有亚基都改变形状，然后与一个分子结合，再全部改变形状，再最后释放那个分子，蛋白质就能显示出边缘循环。｜图片来源：Evelyn Tang et.al

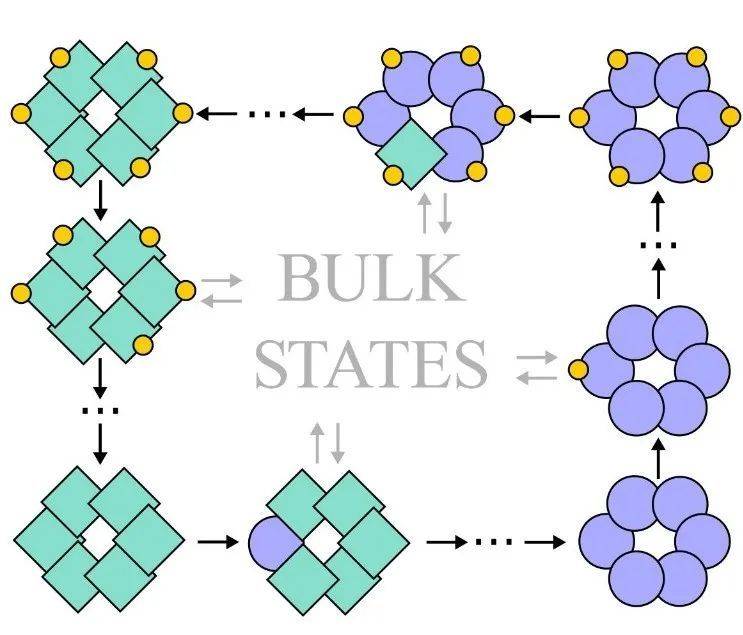
这样的结果意味着，在二维的生物化学反应网络中形成了“静电流”。而且无论这种系统边缘的形状是否有变化，还是系统整体的无序性的改变，这些生物化学“边缘电流”都显现出了稳健性。此外，研究人员还发现，边缘电流的出现与由能源消耗驱动的无效循环的不平衡性有着不可分割的联系。研究人员想要知道，是否就像在量子霍尔系统中那样，生物化学系统中的这种稳健性是否也来自于拓扑。

然而，量子系统中使用的工具并不能直接适用于受经典的随机定律支配的生物化学系统。为此，研究人员在他们的生物化学系统和一种被称为非厄米量子系统的奇异系统之间设计了一种映射。一旦建立起这种映射，用于拓扑量子系统的整套工具就可以为生物化学系统所用了。新的研究证明了，与量子霍尔效应相同的拓扑概念的确可以存在于生物化学系统中，它能够确保相应的生物化学过程的稳健性。

三

新的研究结果为未来开启了一个充满可能性的新领域。由拓扑引发生的稳健性，加上生物化学网络中固有的多功能性，能让科学家有望在这些系统中可以观察到的大量意想不到的现象。

参考来源：

https://www.ds.mpg.de/3763345/210723_topology

https://journals.aps.org/prx/abstract/10.1103/PhysRevX.11.031015

本文来自微信公众号：原理（ID：principia1687），作者：小雨