本文来自微信公众号:混沌大学(ID:hundun-university),授课老师:狄增如(北京师范大学系统科学学院教授、国际系统与控制科学院院士),原文标题:《狄增如独家授课:通过系统科学洞察复杂世界 | 文理学院》,题图来自:unsplash
霍金说:我认为,21世纪将是复杂性的世纪。
的确,我们身处的世界正变得越来越复杂。金融、互联网、人工智能的飞速发展,无不让人眼花缭乱;气候变化、生物多样性丧失、贫富差距拉大等“发展的代价”,也在不断凸显和演化。
生活在如此纷繁的时代,似乎稍不留心就会跟不上世界前进的步伐。那么,我们如何才能透过种种表象,把握时代脉搏并与时俱进呢?
也许,系统科学是一种答案,可以成为人类探索未知的下一个前沿、解锁未来的下一把密匙。事实上,早在80年代,科学家钱学森就说,“系统学的建立,实际上是一次科学革命,它的重要性绝不亚于相对论或者量子力学。”
在混沌大学文理学院的讲堂上,北京师范大学系统科学学院教授、国际系统与控制科学院院士狄增如从复杂科学的现象进入,将社会科学、自然科学的基础性问题结合在一起考虑,试图挖掘复杂表象背后的简单法则。
一、现代科学的知与不知
20世纪,整个人类文明的科学技术飞速发展。从宏观角度来说,人类对于宇宙的认识已经取得巨大的飞跃。简单举例来说:
2013年,我们把宇宙诞生的大爆炸时间点精确到了138.2亿年。
2020年的诺贝尔物理奖有两组得主,一组用爱因斯坦的相对论场方程证明了黑洞的存在,一组切实观察到了银河系中心存在一个巨大黑洞。
2020年11月,嫦娥五号探测器成功发射并返回地球,让我们可以真正研究月球的故事。
从微观角度来说,我们已经知道了宇宙中所有物质最基本的结构单元。除了未知的暗物质和暗能量,宇宙里的所有物质都由6种轻子和6种夸克构成,而稳定物质都是由电子和电子中微子两种轻子,以及上夸克和下夸克两种夸克构成。
可以说,任何物质的结构单元都是完全一样的。这是很深刻的科学认识,也提出了系统性、涌现性的科学问题。
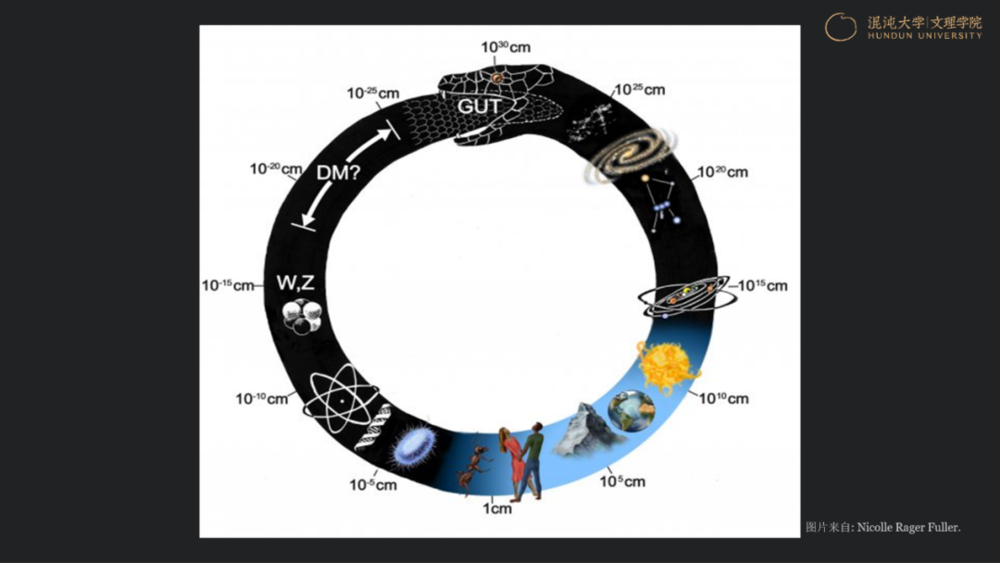
从这条衔尾蛇可以看出,我们对宏观的宇宙演化和微观的物质结构的科学认识已经紧密联系在了一起。然而,对于自己所生活的衔尾蛇中段——时间尺度以分秒计量、空间尺度在厘米到米的量级,是我们应该最为熟悉的世界——却还恰恰缺乏科学认识。
比如,生物学中关于生命的定义完全是描述性的,一般只关注生物的外形、繁殖和新陈代谢方式等,但是,很多关键问题依然悬而未解,对于生命的理解还缺乏真正的科学认识。

生命的起源、意识的来源、复杂的生态系统、群体行为、技术系统,这一切如何运作就是未来科学的挑战所在。其中的核心科学问题是:即使我们对每个个体的性质都很清楚,但当大量个体通过某种组织形式构成一个整体,就会涌现出完全不一样的结构、性质和功能。
物理学家P.W.安德森提出:More is different。多者异也。
“将万事万物还原成简单的基本规律的能力,并不蕴含着从这些规律重建宇宙的能力......当面对尺度与复杂性的双重困难时重建论的假设就崩溃了。其结果是大量基本粒子的复杂聚集体的行为并不能依据少数粒子的性质做简单外推就能得到理解。取而代之的是在每一复杂性的发展层次之中呈现了全新的性质,从而我认为要理解这些新行为所需要做的研究,就其基础性而言,与其他相比也毫不逊色。”
他的观点在美国产生了巨大的影响。上世纪70年代,美国科学界内部激烈争论,要不要建造一座超越欧洲水平的对撞机。安德森说明,复杂性研究尚有很多非常重要的问题值得研究,更多的科学家反思说,也许不应该花费重金、一味探索更远的宇宙,从而一定程度上助力终结了美国的对撞机计划。
今天,信息技术发展加强了人和人、人和物之间的联系。我们的世界越来越小,联系越来越紧密,使我们所面临社会经济挑战的系统性和复杂性也越来越突出。
简而言之,系统科学是研究系统的结构与功能关系、演化和调控规律的科学,是一门新兴的综合性、交叉性学科。
系统科学以不同领域的复杂系统为研究对象,从系统和整体的角度,探讨复杂系统的性质和演化规律,目的是揭示各种系统的共性以及演化过程中所遵循的共同规律,发展优化和调控系统的方法,进而为系统科学在科学技术、社会、经济、资源、环境、军事、生物等领域的应用提供理论依据。
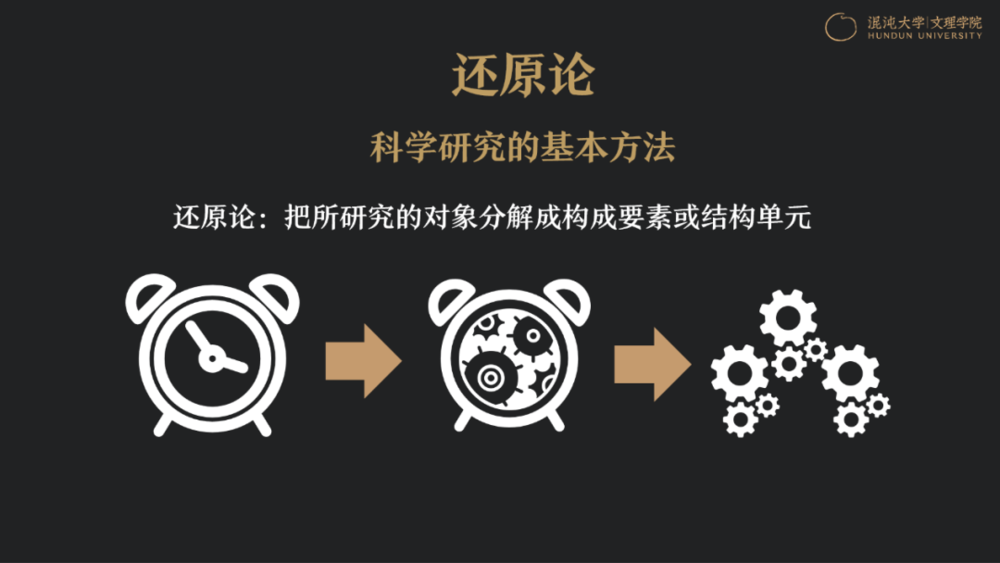
复杂科学研究若想有所获,就必须超越还原论。还原论是曾在20世纪带给我们诸多重要科学发现的研究方法,简单来说,其核心就是,当我们想知道某个物件的结构和原理,首选就是拆掉它。
比如拆掉闹钟,看它如何走字、如何定时;拆掉人体,拆分成运动系统、呼吸系统、循环系统、生殖系统;拆掉水分子,以了解水为什么到100度就会沸腾。
曾经,还原论的巨大成功使它成为科学认识和解决问题的基本线路和方法。比如,我们想解决问题,首先会想到去“分析”它,“分”就是拆,“析”就是拆得更细。由此可见,还原论的科学方法已经潜移默化到我们的血液里。
问题在于,我们能不能超越还原论,把科学成果重新组装,从而认识这个复杂世界?
我们可以通过零部件组装,知道闹钟怎么工作吗?重组每一个心肌细胞,解释心脏为什么会跳?研究大脑神经元,了解我们如何有智慧?观察一只不起眼的小蚂蚁,理解蚁群怎么逢山开路、遇水架桥?

一只鸟的飞翔是力学问题,但是一群鸟就是复杂科学的问题,到现在我们也不知道是怎样的关联和影响让它们形成这样的宏观结构。
1999年,《科学》杂志就“复杂系统——超越还原论”出了一个专辑,提出观点,要想理解生命、发展技术、提升经济,做到可持续化发展,我们方方面面都必须超越还原论,用复杂系统的角度去研究我们身边的问题。
比如,中医的科学化是目前我国非常看重的议题,而中药组分学就是基于还原论的研究路线,即用现在的科学技术手段分析汤药所含元素,找出药效的关键。确实有些中药通过单一要素起作用,比如青蒿素。
但是,中药在本质上讲究的是配伍,即中药里的多种成分遵循自然规律有序地结合,这种结合不是随机搭配、存在质和量的必然规律。所以,还原论的研究线路根本就不符合中医的本质,更不是中医科学化的正确线路。
相对来说,从复杂思维的角度,我们不仅要知道汤药里的要素,更要知道它们之间的关联,并从科学定量的角度把中药的配伍刻画出来,这样才能真正体现中医药的价值。
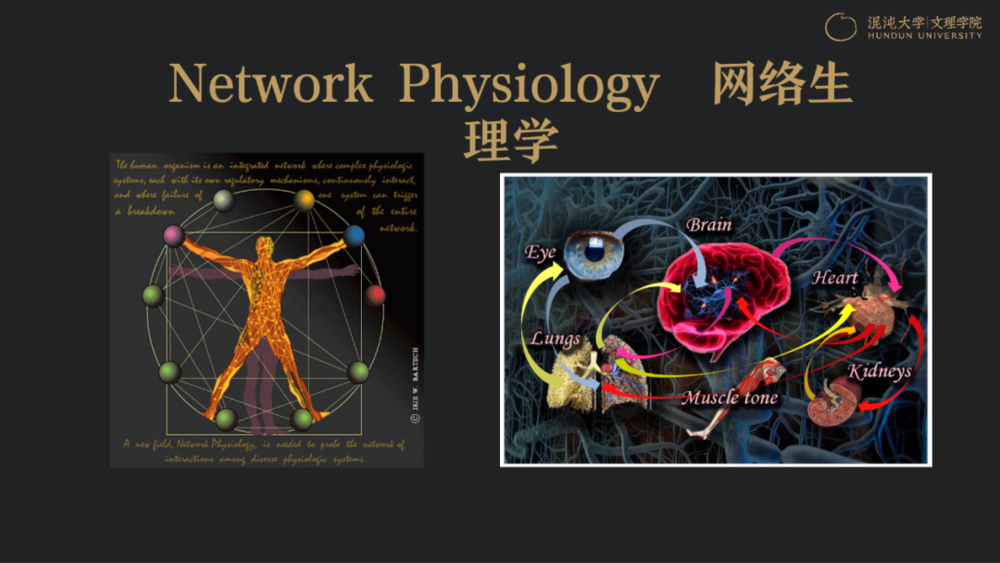
西医理论中,一个人的心肝脾肺胃健康,就说明人体是健康的;而依照网络生理学,即使心肝脾肺胃都健康,它们之间的关系若是不好,人的健康也会有问题。细胞怎么形成组织,组织如何形成人体、提供结构和功能,这些只能从系统科学的角度去研究。
二、生命和自然界中的秩序涌现
复杂科学得以存在,其基础是我们相信在纷繁复杂的系统背后,一定存在统一、普适的科学规律。这套理论可以帮助我们探索生命的起源,进而为我们理解物质和生命带来全新的理念。
宇宙在138.2年亿年前从一片混沌中诞生,然而生命这样有秩序、有灵性的东西是如何由6种轻子和6种夸克构成的呢?按照热力学第二定律,热力学系统总是要朝着平衡态演化。平衡态意味着无序、均匀、低级和简单的发展方向。
孤立系统中的自发过程总是导致体系中熵的增加,意味着系统会自然走向混乱和死亡。而从无序中产生有序、从混沌中涌现生命违背热力学第二定律,超越熵增就必须要从孤立系统走到开放系统。

开放系统受到外界的影响,其内部的不同要素之间也会产生非常强的关联,这是所有复杂科学强调的最重要的观念。不仅生命是有序结构的涌现,我们身边的自然界也有很多这样的例子,卷积云、溶液、动物的心跳和皮肤……自组织令人惊叹的美妙结构和模式随处可见,而它们都只是在开放系统中才能被观察。
自组织理论——沟通物质与生命
个体间的关联有线性和非线性,当我们把关注的对象从孤立系统拓展到开放系统,把单元内部的相互作用从简单的线性推广到非线性,世界就完全不一样了。
普里高津是布鲁塞尔学派的创始人,哈肯是德国的哈肯学派的创始人,他们创立了自组织理论,其最核心的认识就是系统内部由于非平衡和非线性关联变得丰富多彩,能够产生五颜六色、纷繁复杂的结构和功能。

自组织系统的主要特征是:
开放系统,与环境有物质和能量交流;
组元众多,且存在非线性相互作用;
远离平衡态;
涨落是有序结构形成的触发器。
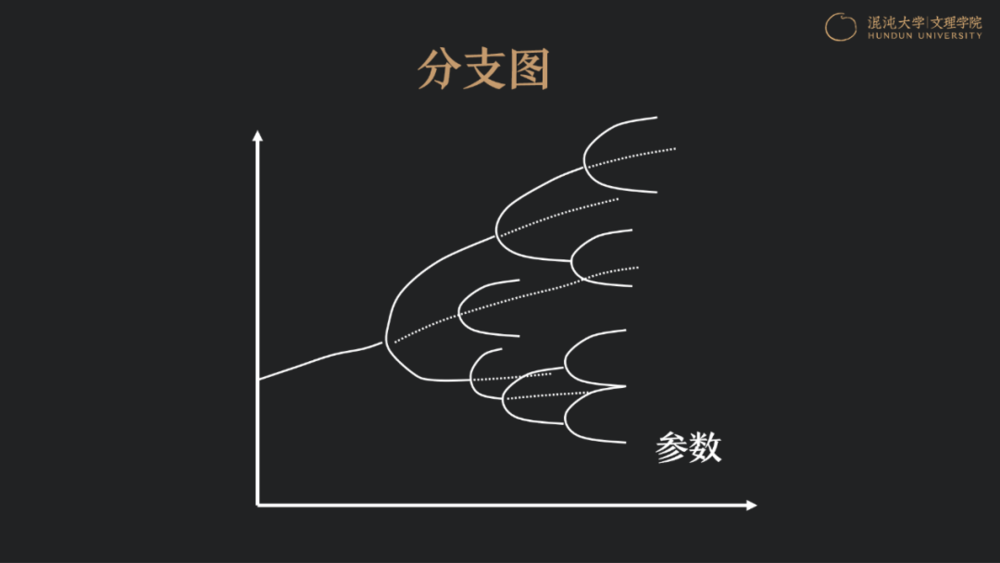
上图就是自组织分支理论中一个最简单的图像:一度无序的系统开放后受到外界环境推动,走向一个新的状态,涌现出有序的结构,而这样的分支过程可以连续进行下去。这样的数学模型,可以帮助我们加深对于自然领域中结构的认识。
自组织理论在生物、社会和经济等领域里有非常多应用,为其研究提供了一个共同的科学概念和理论。
在复杂科学里,基本的研究方法分三个层次:
自顶向下的宏观层次的动力学方法。这是研究复杂系统一个基本的研究线路。东方文化天然就有这样的系统观和整体观,比如中医对人的观察和感觉就是把人看作一个系统和整体。
自底向上的多主体方法。先关注个体,再看它们的相互关联能够产生什么宏观影响。比如了解金融市场每一个投资者的行为和他们之间的关联,然后研究成千上万的投资者会造成什么样的宏观市场表现。
中观层次的随机方法。
复杂系统的科学认识基本上都适用自顶向下的研究方法,比如对于一箱子理想气体,我们不需要知道每一个分子的位置和速度,它们的整体宏观表现才是我们关心的。
三、混沌奇迹——随机与秩序的统一
1. 动力学——刻画系统演化的工具
动力学的方法可以用来描述系统的宏观性质和演化,从牛顿动力学发展而来,研究的基本路线是关注质点的位置、速度,以及它们的变化,这套理论起初被用来研究星星的运动,后来延伸到大气动力、气候变化、人口增长及金融市场等等。

把动力学应用到复杂系统,最典型的就是马尔萨斯模型,马尔萨斯模型解出来是人口将呈现指数型增长,虽然模型不能完全模拟现实,但模型可以用最简单的方法,准确挖掘出影响系统变化最本质、最内核的因素,马尔萨斯模型也因此成为通过政策控制人口的理论基础。
然而,这个模型没有考虑一个重要因素:环境制约。任何一种生物都会受到环境制约,纳入这一考量因素之后,就会得到Logic增长带来的S型增长曲线。后来,这一增长曲线被应用在城市演化、社会进步等诸多场景。
再比如开普勒问题,也就是著名的二体问题。
它的发现给了人类一种优越感,自以为已经知道了世界的所有规律。整个宇宙的演化看似都在牛顿力学的左右之下,再加上万有引力和电磁相互作用,我们似乎可以确定,只要知道宇宙每一个分子和原子当前的位置和速度,它所有的过去和未来都会展现在我们眼前。
拉普拉斯决定论的观点是,“我们可以认为宇宙的现在是由它的过去来决定的;现在也是决定未来的原因。如果有一位智者在某一时刻获知了自然界一切物体的位置和相互作用力,并且他具有超常的数据分析能力,那么他就可以把宇宙这个最庞大的物体直至到原子这个最细微的颗粒全都囊括到一个公式中去。对于这位智者来说,没有什么东西是不确定的——宇宙的未来会像它的过去一样完全呈现在他的眼前。”
但是,近代复杂科学的研究使我们意识到,人类距离对于现实有确定性的认识还差得很远。
2. 蝴蝶效应——确定性的终结
我们想预测的最简单的问题就是太阳、地球和月亮之间的关系,也就是三体问题。
19世纪,欧洲是整个科学技术的中心,瑞典国王悬赏,征求太阳系稳定性问题的解答,期望解决天体力学中的N体问题。但当时,我们耳熟能详的大科学家——牛顿、欧拉、拉格朗日、拉普拉斯、泊松却都没能解开谜题。
最后,解决这个问题的是彭加莱,他是历史上最后一个数学通才。数学论断可证明或证否,证否即是无解,彭加莱把三体问题证否了。
在解决上述问题的过程,彭加莱也发展了在宏观角度运用动力学研究复杂系统的方法,非常具有革命性。曾经,我们研究问题关心的都是定量,想知道每一个质点的轨迹。但既然这不可能,我们就必须换一个角度研究——从定量转为定性,不必关心具体的轨迹,而是观察当时间趋于无穷的时候,它是会停在一个地方,还是会跑到无限远。马尔萨斯的人口模型、无限增长和单摆周期运动都是长期的定性行为。
此外,还有一类系统,既不跑到无限远、也不停下来,而是无时无刻地在运动,而且不重复、无周期。比如天气系统。
美国麻省理工学院教授洛伦兹奉献毕生研究“长期天气预报”。1961年底某一天,洛伦兹在办公室里把一个数据输入到一台及其缓慢的Royal McBee计算机,企图重复验证上一次的计算结果。他知道这需要等一个多小时,便踱进了学院旁边的一间小小咖啡馆……
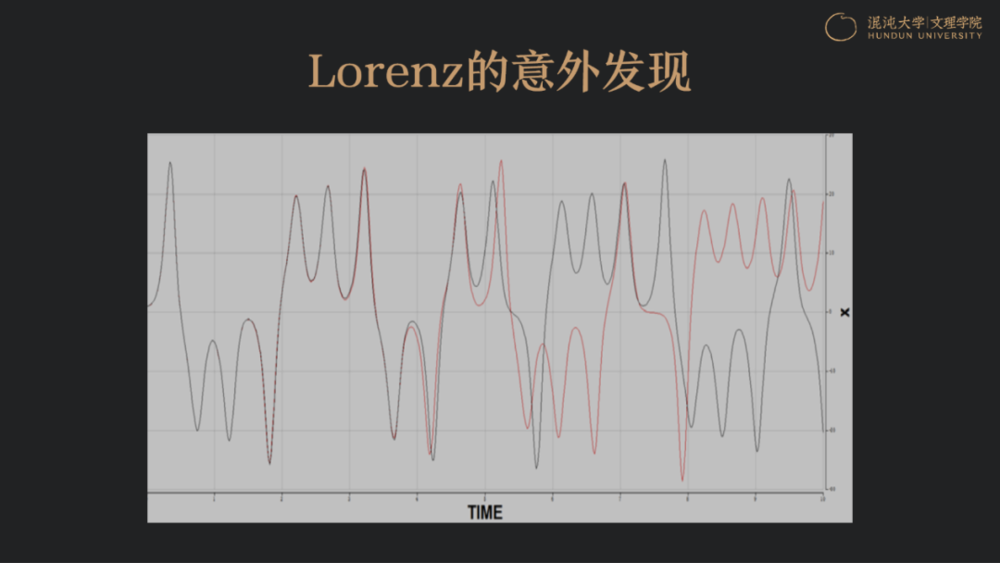
回来之后,洛伦兹意外地发现计算结果与上一次有天壤之别。
排除了计算机故障的可能性后,他终于找到了理由:在第一次计算中,他输入的初始值是0.506127;在第二次计算中,他图省事,输入了0.506。按理说这两者相差甚微,结果应该只有微小差别,但由于“系统对初值的敏感依赖性”,一个微小的初始误差随着反复迭代计算,酿成了巨大差异的后果。
这一意外的发现,就此开启了混沌科学。
洛伦兹模型后来演化成了洛伦兹吸引子系统,在该系统中,从任何的初始条件都无法准确地预测轨迹。洛伦兹吸引子的整个形状像一只蝴蝶,洛伦兹在论文中提到,“在巴西的一只蝴蝶拍打一下翅膀,会在德克萨斯引起一场龙卷风吗”,复杂性科学中著名的“蝴蝶效应”就来源于此。

美国博学家、开国元勋之一本杰明·富兰克林曾写过一首诗描写了这么一个场景,在一次古代战争中,一个通讯兵去传递重要的作战讯息,出发的时候发现一块马蹄铁的一个钉子松了,他没理会。然而,这个马蹄铁跑到半路坏了,马跑不动了。后来,通讯兵被敌人抓住,情报没送到。再后来,这场仗打输了,这个国家就灭亡了。这就是蝴蝶效应的典型案例,说明小的事件能够带来大的影响。
3. 无序中的有序——混沌中的秩序
确定性的规则完全有可能带来随机的结果,这是复杂科学研究给我们世界观带来的最大冲击。我们由此认识到,必须对牛顿力学建立的、确定论性的世界观加以变革。
理解生命的一个核心问题在于理解复杂系统的状态变化,以及它能产生的有序结构。
混沌的行为和结构中存在丰富的秩序,仍然以人口模型作为例证。种群的增长可以被看作一个离散的事件,第一代有10只兔子,1生1的话,第二年变成20只,第三年变成40只,这就是最简单的马尔萨斯指数增长模型。
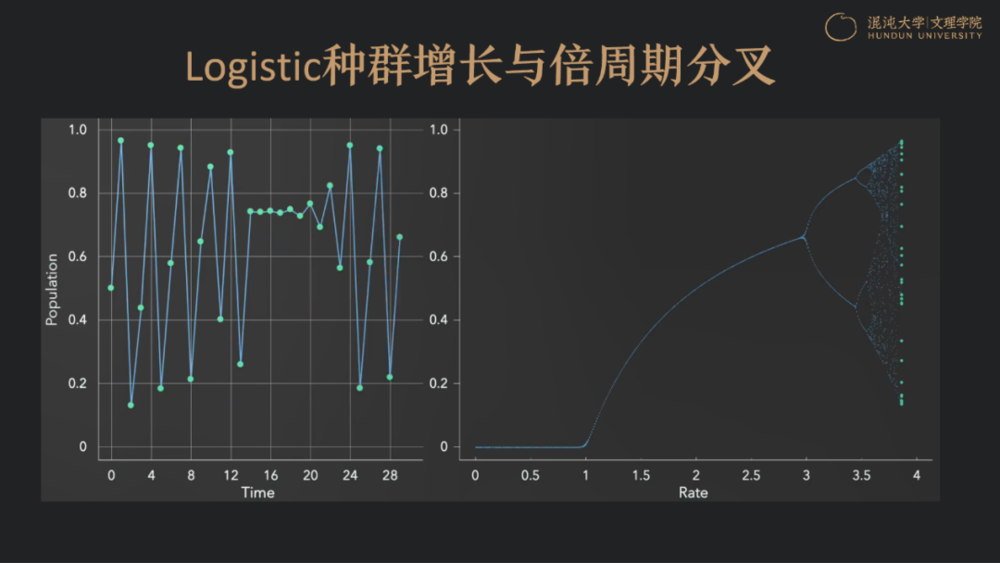
另外一个模型是Logistic种族增长模型与倍周期分叉,其特点是有约束。这个模型只有一个参数,就是种群增长率λ。繁殖能力强,λ就大;繁殖能力弱,λ就小。λ低于1的时候,这个种群是维持不住的,不管开始有多少,最后都会变成0。当λ大于1的时候,一群兔子就会达到稳态,每年的增长和死亡将维持在一个固定值,是可预期的。
但是,如果繁殖率继续增加,整体状态就不再是一个稳定的点,而是一个周期解。比如今年我有5只兔子,第二年会涨到15只,没有那么多草料了,又会变成了5只。于是就在5只、15只、5只、15只之间跳动。若继续增加λ,就可能变成4倍的周期,四年一轮回;再继续的话,一定是4变8,8变16。而这样的过程如果延续,兔子种群的演化数量也会进入到混沌区。
从这个例子,我们看到,简单的数学迭代模型在特定的参数条件之下变成混沌状态,小的扰动能够带来大的偏差。
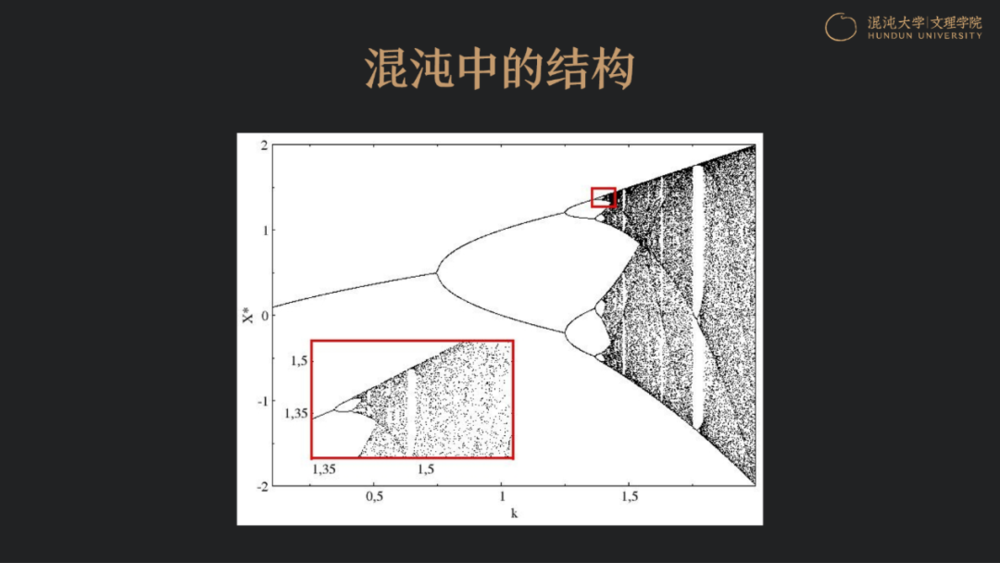
总结来说,要对身边的复杂现象获得科学认识,就必须超越还原论。因为所有的复杂现象都来自于大量构成系统的单元之间相互的影响和关联。若用还原法把它们一个个分开,那将无法对系统的性质获得科学的认识,无论是生命的产生,还是有序结构的涌现。
四、混沌为什么如此引人注目?
混沌理论揭示了简单性和复杂性、有序和无序之间存在精妙关联,从而沟通了科学与生活,帮助我们产生科学认识。
曾经,很多科学家认为生命现象有其独特规律,不是物理规律能够理解和认识的;但是,自组织理论沟通了物质和生命,它的发展揭示了物质和生命等复杂系统在底层上有统一的、可把握的、普适的规律。这是一个非常重要的科学启示。
宏观动力学方法是我们研究系统演化最基本的科学工具。然而,虽然工具是确定性的,它所揭示出来的演化规律却是随机的、混沌的。比如,牛顿力学的运动规律是确定性的,但天气预报却难有准确的预测。
从思想方法上,复杂性科学研究带给我们什么呢?
世界的本质是非线性的,线性的关联是对于世界太简化的抽象,我们思考世界的本质、理解复杂的现象,一定要从线性走向非线性。
复杂的现象背后可能具有简单的规律,简单的规律背后可能是非常复杂的现象。系统性科学研究让我们对于系统的最终取向有了一个定性的了解和把握,不再预期精确地描述单位的运动轨迹,不再试图精确地给出长期预测,因为一个意想不到的小概率事件往往可以影响大局。
复杂科学的思想方法有助于我们在观察复杂系统时保有更理性的态度,当现实不按照我们因果分析出的方向发展时,让我们可以在混沌系统中找到安慰,力争做到定性的把握、成为时间的朋友。
本文来自微信公众号:混沌大学(ID:hundun-university),作者:狄增如(北京师范大学系统科学学院教授、国际系统与控制科学院院士)

