统计物理、无序系统和神经网络

本文来自微信公众号：科学杂志1915 （ID：kexuemag），作者：黄海平，题图：2021诺贝尔物理学奖得主乔治·帕里西，来源：视觉中国

2021年，诺贝尓奖委员会决定将物理奖颁发给研究复杂系统的三位科学家，一时引起无数诧异和哗然，这是诺贝尔奖首次颁发给复杂系统研究领域。

帕里西（G. Parisi）因其对无序和随机现象理论的革命性贡献而独享一半奖金，诺贝尔奖委员会给他的颁奖词是“他发现了从原子到行星尺度的物理系统中无序与涨落的相互作用”。

帕里西是非常典型的理论物理学家，由于他研究的领域数学物理味道较浓，并且十分抽象，故即使在理论物理圈子里，他也不是那种妇孺皆知的科学家。

他的代表性工作包括随机量子化，自旋玻璃理论，界面生长动力学普适类，随机气候模型和鸟群群体运动的涨落标度等。

在获得诺贝尔奖之前，他几乎拿遍了作为顶级理论物理学家该拿的所有奖项：玻尔兹曼奖、狄拉克奖、费米奖、丹尼海涅曼数学物理奖、拉斯昂萨格奖、沃尔夫奖等。获奖领域横跨统计力学、粒子物理、数学物理、自旋玻璃等。

一、帕里西的科学探索起点

帕里西于1948年出生于意大利罗马，爷爷和父亲都是建筑工人，因此家族曾希望他将来做一名工程师。

然而，青少年时代的帕里西喜爱阅读科学书籍，被书中复杂的抽象知识所深深吸引。鉴于20世纪中叶物理学的蓬勃发展，他决定研究物理，并且深信自己有能力去解决一个具有挑战性的物理问题。

大学时，他成为粒子物理学家卡比博（N. Cabibbo）的学生。卡比博因发现“卡比博角”闻名于世，也称得上是诺贝尔奖级别的大师。

帕里西后来回忆，他的导师是那个时代罗马最聪明的理论物理学家。

1970年帕里西取得博士学位后，先在弗拉斯卡蒂国家实验室工作了10年，之后来到罗马第二大学担任理论物理学教授。1992年起至今为罗马第一大学的量子理论教授，研究重点是量子场论、统计力学和复杂系统。

2013年帕里西获得《自然》（Nature）周刊颁发的杰出导师奖时，提到他的导师，说他导师曾经说过，科学研究的目的就是享受解决问题的乐趣，这可能是卡比博留给帕里西最宝贵的财富。帕里西在他的科学生涯中将这句话体验得淋漓尽致！

二、对无序系统理论的开创性贡献

1970年代末期，帕里西的研究兴趣转向无序系统的理论研究，因为这类系统的复杂性深深吸引了帕里西。无序系统理论研究始于1980年代，帕里西是先行者之一。

1. 复杂无序系统

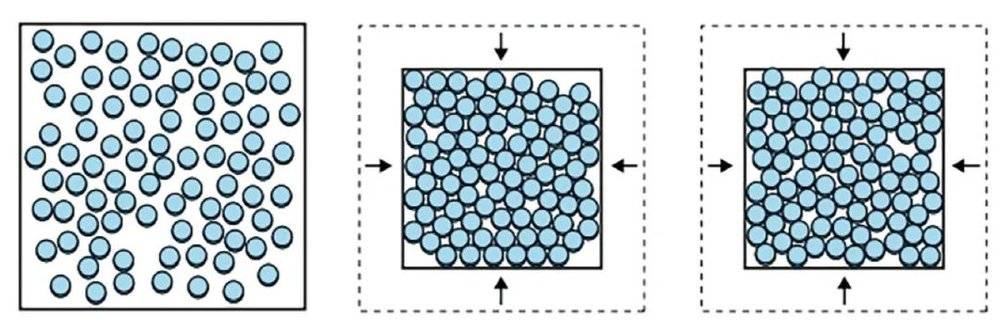
以气体为例，气体中的粒子可以被视为小球，其飞行速度随温度的升高而增加。当温度下降或压力升高时，小球首先液化，然后凝固。形成的固体通常是一种晶体，小球在晶体中以规则的模式排列。

然而，如果这种变化发生得很快，小球来不及规则排列，从而形成一种无序的图案，即使液体进一步冷却或挤压在一起，图案也不会改变。

如果重复实验，尽管变化以完全相同的方式发生，但是每次都会呈现全新的图案。

复杂无序系统的简单示意

2. 自旋玻璃

我们可以把这些小球形成的图案看作是玻璃或颗粒材料（如沙子或者砾石）的简化模型。

帕里西最初研究的是另一种类似系统——自旋玻璃，这是磁性合金材料的一种亚稳定状态。自旋玻璃是典型的无序系统，在经典统计物理里，自旋可以标记粒子的离散状态，比如向上或向下。

一般的磁体中，所有磁矩的自旋都指向同一个方向，其分布是长程有序的。而自旋玻璃中处于格点上的自旋的相互作用是完全随机的，这种随机性导致自旋取向出现阻挫效应（frustration effect），即自旋的取向难以满足局部能量最低的要求。

自旋玻璃的一个显著特征是宏观平均磁矩消失，但存在自旋玻璃序。这里的“玻璃”一词实际上是长程无序状态的代名词，表示这种无序状态类似于一般的玻璃。

在帕里西关于自旋玻璃的书中的介绍，他写道：研究自旋玻璃就像看莎士比亚的四大悲剧。

如果你想跟两个人同时做朋友，但是这两个朋友之间互相敌视，这会让人沮丧。这类场景在古典悲剧中更是突出，如果感情最要好的朋友成为了敌人在同一个舞台上相遇，怎样才能把房间里的紧张氛围降到最低？

3. 自旋玻璃的研究背景

玻璃态的物理本质直到今天依然悬而未决。

50多年前，物理学家为了研究玻璃态提出了自旋玻璃的概念。爱德华兹（S. Edwards）和安德森（P. Anderson）于1975年提出短程相互作用的自旋玻璃模型 ^[1]。

同一年，谢灵顿（D. Sherrington）和柯克帕特里克（S. Kirkpatrick）提出自旋玻璃的平均场模型（简称S-K模型）^[2]，他们的工作标志着物理学家对自旋玻璃系统的研究拉开了序幕。

S-K模型将短程模型推广到全连接的情形，即每个自旋都同其他自旋两两连接。现在知道S-K模型的平均场性质（包括动力学行为）存在数学解析形式，这可能是帕里西非常着迷于此类模型的原因之一。

短程相互作用  暂且忽略虚线的贡献，粗线代表铁磁相互作用（要求相邻自旋朝向一致），细线代表反铁磁相互作用（要求相邻自旋朝向相反），这样左上格点的自旋难以取合适的朝向，从而使得体系的能量最低。

全连接平均场模型  每个自旋（圆形格点）都与其他自旋两两连接。

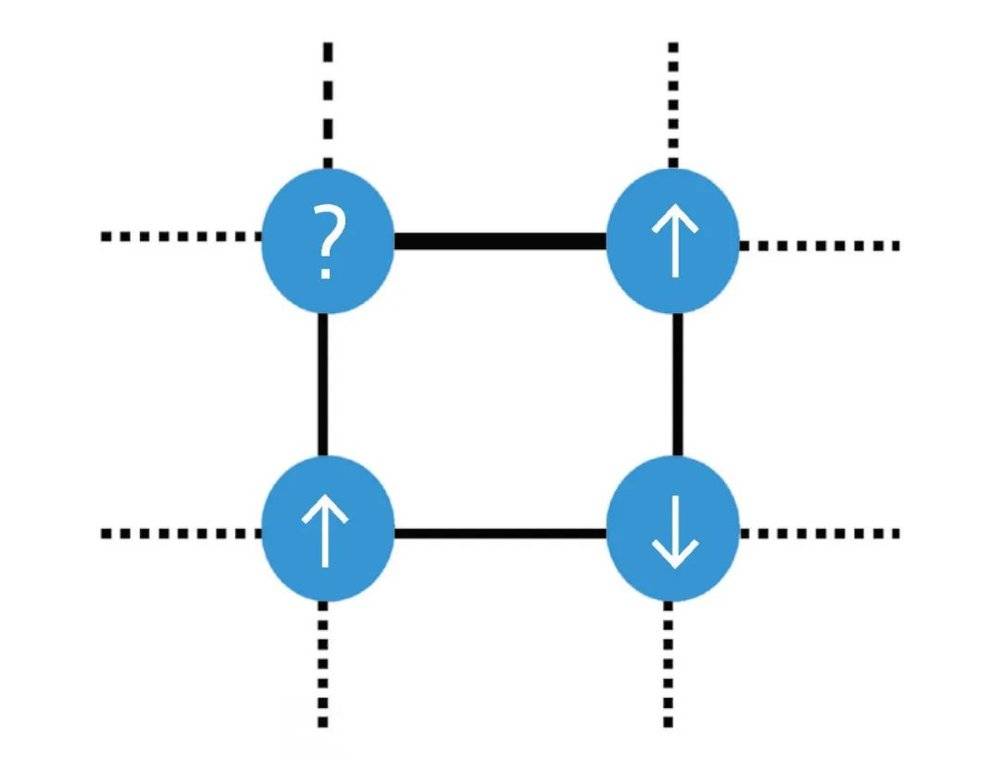
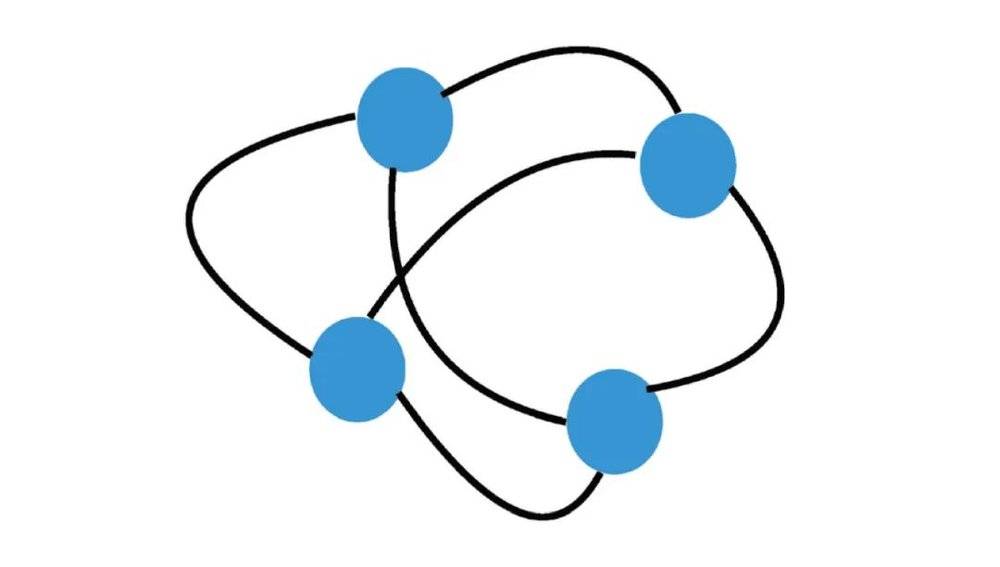
当时困扰物理学家的一朵乌云是，S-K模型的低温熵为负值，这强烈违背了物理直观，因为自旋取向只有两个方向（离散取值）的系统的熵不可能为负（系统的构型数是可数的）。1978年，对S-K模型的稳定性分析证明，S-K模型的低温解是不稳定的 ^[3]。

那么，一个重要的问题随之而来，S-K模型的负熵危机根源在哪？

次年，这个问题被年轻的帕里西解决 ^[4]，当时他年仅31岁。这似乎再次印证了“自古天才出（青）少年”！

4. 帕里西的魔法

针对自旋玻璃系统，帕里西提出了复本对称破缺（replica symmetry breaking， RSB）的概念，发展了一套有效的数学方法，并给出了一个精确的理论解。

其物理本质就是将原有模型自旋之间的复杂相互作用，转换为同一模型的多个拷贝（即多个复本）间的相互作用。这样，复本之间就存在一耦合矩阵，如果这一矩阵的非对角元素均同（对角元素显然一样），那么这个均同的元素就是统计物理的序参量，从而刻画了前面提到的自旋玻璃序。

帕里西以天才的想象力引入了破缺，即正确的复本矩阵应该在对角线上出现不断分块结构，每一次分块将引入新的序参量；而且，对于S-K模型，这种分块是无穷多次的。这样，序参量将变成连续的函数。

帕里西发现，只有这样，S-K模型的低温熵才能在复本对称破缺无穷多次之后趋于零，负熵危机才得以解决，也不违反热力学第三定律。

复本对称破缺的数学表述  3个大方块分别表示不同层次物理近似的复本矩阵。(a)最低阶的复本对称近似，即所有非对角矩阵元一样；(b)一阶复本对称破缺，即在对角线上分出n/m₁个（图中是3个）m₁×m₁块矩阵，因此比(a)情形多出一个额外的自旋玻璃序（块矩阵的非对角元素）；(c)二阶复本对称破缺，每个块矩阵又以同样方式被细分为m₂×m₂的块矩阵 ^[5]。

随着帕里西与合作者几十年如一日的深入研究，复本对称破缺的物理意义逐渐明朗。这一猜想在20多年后被法国数学家塔拉格兰（M. Talagrand）证明 ^[6]，成为物理学史上为数不多的经典案例！

帕里西后来总结道：当物理学家使用数学时，他们以更宽松的方式使用它（when physicists use mathematics， they use it in a looser way）。

这十分贴切地形容了物理学家眼中数学与物理的关系：物理是数学的实在。

例如，2015年，随机激光物理系统中的实验也证实了复本对称破缺的概念 ^[7]。物理学家在解决物理问题的过程中，擅长在物理直觉指引下做近似；而最不可思议的地方是，这种近似最后却是精确的。这样的思维，也许可以总结为不求严格，只求精确。在21世纪复杂系统研究中，这样的研究风格可以说是必需的。

笔者在中国科学院理论物理研究所读研究生时，有幸参加了2008年在北京举办的自旋玻璃及其交叉学科的国际研讨会，笔者至今仍记忆犹新。

在帕里西报告结束时，有人向他讨教他是如何开创复本对称破缺的思想时，帕里西笑着回答道：“因为那时候不用到处开会，我能专注于一件事情”（大意）。这说明，要完成一件有深刻影响力的事情，需要的专注与大量的时间和精力上的投入等同。

当然，前提是科学家关注重要的科学问题，并且与某个研究领域一起成长（不是老化）。可见科学家一生能做成一件重要的事情，就已经非常了不起了！

帕里西开创的领域长期来看是小众方向，但他几十年如一日地坚持，让自旋玻璃研究的涓涓细流终成大河，这种精神尤其值得有志于科学探索的年轻人学习！

三、复本对称破缺对交叉学科的影响

复本对称破缺本属于非常抽象的数学物理概念，但40年来，我们难以置信地看到它广泛地存在于各交叉学科领域，甚至影响了概率论的研究分支。

接下来简述一下复本对称破缺在神经网络及优化问题研究方面的影响。

神经网络是当前科学研究范式（AI for Science）的基本工具，而优化问题更是非常古老的学科方向。

1. 神经网络的理论研究

帕里西开创的复本对称破缺的研究范式，是其获得诺贝尔物理学奖的重要原因。该范式在1980年代中期就已延伸到人工神经网络的理论研究。这对于当前人工智能的基础理论研究不乏具有参考价值。

早期的研究集中于分析联想记忆网络。这类网络是根据神经科学的赫布律来设计的简单循环神经网络，它能够提取部分被破坏的记忆模式，从而模拟大脑的联想记忆功能。

复本方法的主要贡献在于解析了联想记忆的相图，发现了记忆相、顺磁相和自旋玻璃相，并且发现通过记忆相的转变都是一级相变 ^[8]。

这个工作使得统计物理第一次能够深刻理解复杂的神经网络结构与功能之间的关系，并由此开启计算神经科学这一学科。

做出这一开创性工作的科学家之一，意大利理论物理学家阿米特（D. Amit）更是在1989年就出版了相关学术专著，将其一生都贡献给了计算神经科学的早期发展，培养了很多这一领域的领导者。

另一科学家佐姆波林斯基（H. Sompolinsky）在以色列创建了埃德蒙和莉莉·萨夫拉脑科学中心，并大力发展神经物理学，成为了横贯统计物理、神经网络和脑科学领域的大师级人物。 

同一时期，受阿米特影响的粒子物理学家阿博特（L. Abbott）也在1990年代转向神经网络和脑科学研究，随后在哥伦比亚大学创建了享誉世界的扎克曼大脑行为研究所，培养了这一领域相当活跃的很多年轻学者。

同在1980年代中期，加德纳（E. Gardner）也以一己之力创建了在感知机（监督学习的典型网络）中的加德纳理论 ^[9]，该理论也是基于复本分析的研究范式，其强大之处在于能够定量计算神经网络计算的物理极限，比如存储容量、最小数据量、算法学习极限等 ^[5]。

1995年，弗朗兹（S. Franz）和帕里西为研究自旋玻璃提出了Franz-Parisi势 ^[10]，巧妙地将统计物理构型空间的几何结构纳入热力学势函数的计算。

2014年，笔者将Franz-Parisi势用于分析感知机学习的计算复杂性起源，揭开了人工神经网络态空间的几何分析序幕 ^[11]。随后学界提出局域熵的概念 ^[12]，拓展了人们对神经计算的认知边界。

传统的平衡态分析显示，这些几何孤立的态基本是零熵的；然而，经验设计的学习算法动力学往往被态空间的少数稠密区域所吸引，而这些区域对神经网络的泛化（即举一反三能力）性能有关键性的影响 ^[12]。

除此之外，复本方法还可用于对无监督学习（即无师自通）的研究。

笔者从2015年开始着力于这方面的理论研究，用简明的数学和清晰的物理图像勾勒出学习过程的本质是自发对称性破缺 ^[13]。这种类型的研究还有很多，都与帕里西在自旋玻璃理论的开创性研究息息相关。

在近40年来人工神经网络的理论研究中，复本方法及复本对称破缺的概念扮演着不可或缺的角色。如今，无论在机器学习或神经科学有建树的科学家中，有相当一部分在职业生涯早期曾接受过统计物理或物理学的严格训练。

在帕里西获得诺贝尔奖之际，许多计算神经科学家或理论机器学习学者表达了对他的祝贺和感激，因为帕里西的思想促成了如今神经网络的理论研究这一交叉学科的繁荣！

2. 组合优化算法的物理分析

21世纪初，帕里西与合作者系统地提出空腔方法 ^[14]，这是与复本方法相辅相成的物理学基本方法。

空腔方法的本质在于分析稀疏因子图（这类图一般有两种节点，一种代表变量或自旋，另一种代表约束或相互作用；典型的计算机科学问题，比如组合优化的随机k-SAT问题就可映射成这样的物理问题）时，通过引入图上节点的虚拟缺失，构造空腔概率的迭代方程，从而求解体系的自由能等物理量。

这类组合优化问题的复杂性也深深吸引帕里西对其进行深入系统的研究。

值得一提的是，他与合作者发现，处于NP-完备类的随机k-SAT问题（k可以理解为自旋的多体相互作用，SAT可以理解为求解能量基态）也存在复本对称破缺相，并且在复本对称破缺思想的指导下，帕里西与合作者提出全新的算法——调查传播法（survey propagation），求解组合优化SAT问题基态的极限逼近理论阈值 ^[15]。

为了表彰他们的贡献，美国物理学会在2016年将统计物理学界的重要奖项“昂萨格奖”授予帕里西与其合作者。这显示了统计物理与计算机科学甚至信息科学的基本问题存在着深刻的联系。

3. 复杂系统的研究路在何方：智能起源

当今， 非常复杂的两类系统——以连接主义为代表的人工智能和人脑，仍然缺乏从原理层面上去理解的突破。其中人工智能毫无疑问已经在重塑人类社会经济的方方面面，而人类对于大脑的理解也必将对社会文明产生不可估量的影响。

最近，科学探索奖历届得主评选出的十大科学技术问题的前3个分别为：①人类的意识，以及学习和记忆的生物基础从何而来；②人脑和机器是否能实现直接通讯；③通用人工智能是否能实现。

寻找这些问题的答案并非易事，尽管最后答案可能很简单。 

统计物理方法是一座架起微观作用到宏观涌现的桥梁，而帕里西在无序系统研究的奠基性贡献，将指引物理、数学、机器学习与理论脑科学交叉方向的科学家破解人工智能和人脑的奥秘。

机器智能和生物智能是由非常复杂的组元（比如神经细胞、神经突触等），通过时空多层级的相互作用所形成的集体行为，其中精确的数学机制很难一目了然。

在这条艰辛的求索道路上，兼具物理深刻性和数学美的理论无疑将开启本世纪在认知科学方面的科学革命，让从第一性原理出发设计智能世界变成了可能。

也只有到了那个时刻，就像麦克斯韦从其方程组导出光是电磁波那样，人类文明也必将步入一个崭新的时代！

参考资料：

[1] Edwards S F， Anderson P W. Theory of spin glasses. Journal of Physics F， 1975， 5(5): 965-974. 

[2] Sherrington D， Kirkpatrick S. Solvable model of a spin-glass. Physical Review Letters， 1975， 35(26): 1792-1976.

[3] Almeida J， Thouless D J. Stability of the Sherrington-Kirkpatrick solution of a spin glass model. Journal of Physics A General Physics， 2001， 11(5): 983.

[4] Parisi G. Infinite number of order parameters for spin-glasses. Physical Review Letters， 1979， 43(23): 1754-1756.

[5] Haiping Huang. Statistical mechanics of neural networks. Singapore: Springer， 2022. 

[6] Talagrand M. The Parisi formula. Annals of Mathematics， 2006， 163: 221.

[7] Ghofraniha N， Viola I， Maria F D， et al. Experimental evidence of replica symmetry breaking in random lasers. Nature Communications， 2015， 6: 6058.

[8] Amit D J， Gutfreund H， Sompolinsky H. Storing infinite numbers of patterns in a spin-glass model of neural networks. Physical Review Letters， 1985， 55(14): 1530.

[9] Gardner E. The space of interactions in neural network models. Journal of Physics A-Mathematical and General， 1988， 21: 257-270.

[10] Franz S， Parisi G. Recipes for metastable states in spin glasses. Journal de Physique I， 1995， 5(11):1401.

[11] Huang H P， Kabashima Y. Origin of the computational hardness for learning with binary synapses. Physical Review E， 2014， 90(5): 52813-52813.

[12] Baldassi C， Ingrosso A， Lucibello C， et al. Subdominant dense clusters allow for simple learning and high computational performance in neural networks with discrete Synapses. Physical Review Letters， 2015， 115(12): 128101.

[13] Hou T， Huang H P. Statistical physics of unsupervised learning with prior knowledge in neural networks. Physical Review Letters， 2020， 124(24): 248302.

[14] Mézard M， Parisi G. The Bethe lattice spin glass revisited. The European Physical Journal B-Condensed Matter and Complex Systems， 2001， 20(2): 217-233.

[15] Mézard M， Parisi G， Zecchina R. Analytic and algorithmic solution of random satisfiability problems. Science， 2002， 297: 812-815.

本文来自微信公众号：科学杂志1915 （ID：kexuemag），作者：黄海平