本文来自微信公众号:科学杂志1915(ID:kexuemag),作者:李新洲(上海师范大学天体物理中心教授),首发于2021年9月24日,头图来自:FERMILAB
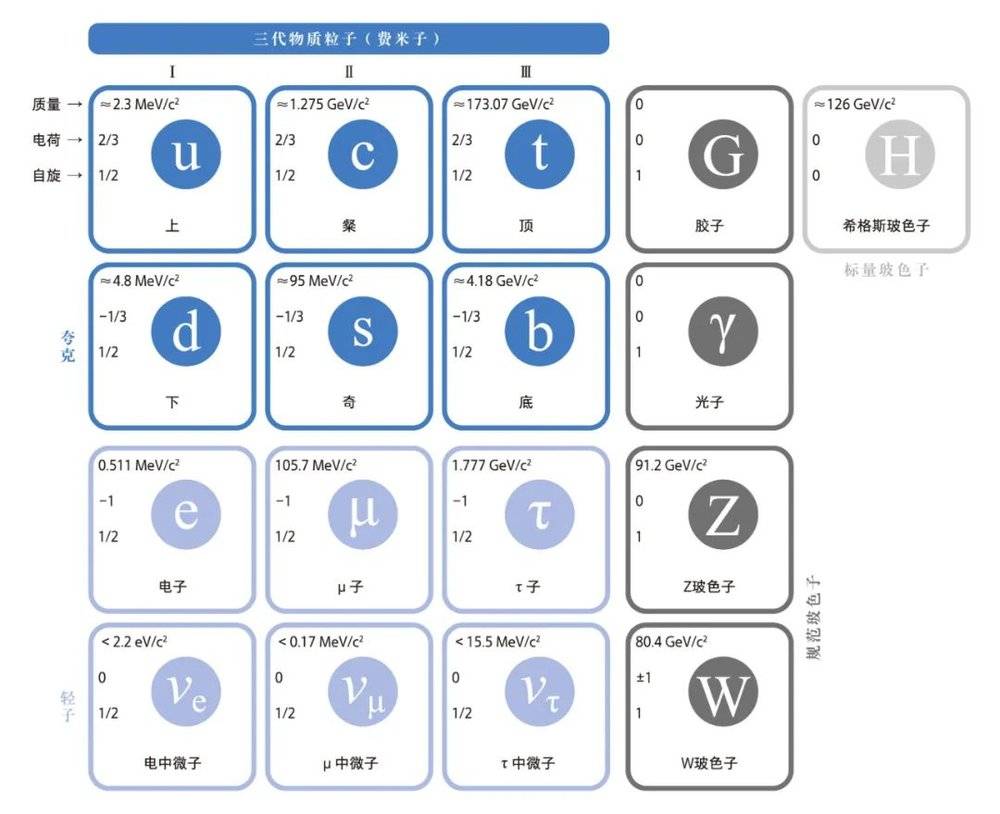
2021年4月7日,《物理评论快报》和《自然》分别刊登了µ子磁矩的最新实验结果,与理论预言的结果却有十亿分之一的差别。这个差别虽小,但令物理学家激动不已。µ子是什么呢?电子和中微子是现在称作“轻子家族”的第一代成员。与电子性质相仿的µ子是第二代轻子,它是在1937年发现的,µ子是辐射到地球表面的宇宙线的主要成分。µ子除了质量比电子大约重200倍以外,其余性质几乎都与电子一样。
一、轻子家族
不同种类的轻子称为轻子的味,或者可以说,轻子带有一种“味”量子数。轻子有6种味,其中3种带有单位负电荷,分别是电子、µ子和τ子,电子最轻而τ子最重。对应它们的分别是3种中微子:电中微子、µ中微子和τ中微子。轻子和夸克都是费米子,它们的自旋都为1/2。对轻子来说,倘若你将右手大拇指指向它的运动方向,其余4指弯曲起来表示它的转动方向,就称它为右旋的;如果对左手成立这种规律,就称它为左旋的。
每种轻子都有它对应的反轻子。反轻子与对应的轻子有相同的质量和自旋,但是在其他性质上有相反的数值。电子是绝对稳定的,因为在强、弱、电磁和引力这4种基本相互作用过程中,电荷都遵循守恒定律,而且电子也不能衰变成质量比它小的带电粒子。µ子比电子重,所以µ子在百万分之一秒内衰变成电子、电反中微子和µ中微子。τ子的平均寿命更短,大约是3×10-13秒。物理学家将3代轻子记成下述形式:
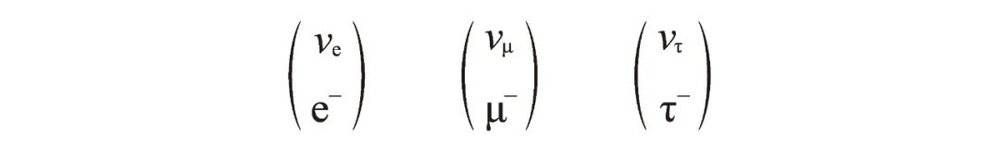
轻子如此配对,自有其深刻的含义:用数学语言讲,它们都是弱同位旋群SU(2)的基本2重态。S是指特殊的,U是指幺正的,SU(2)是一个2维特殊幺正群。
与轻子理论差不多同时发展起来的,是强子的“夸克模型”。开始时,物理学家认为只有3种夸克,后来陆续发现了粲夸克和底夸克。1995年,发现了第6种夸克顶夸克。
夸克同轻子一样,可以是左旋的,也可以是右旋的。夸克的电荷都是电子电荷的分数值,下夸克d、奇夸克s和底夸克b的电荷是-1/3,而上夸克u、粲夸克c和顶夸克t的电荷是+2/3。相应的反夸克所带的电荷则是夸克电荷的相反数。夸克也参加弱作用,在这种作用中,一种夸克味可以变成另一种。例如在β衰变中,中子的一个d夸克变成了u夸克,同时释放出一个电子和一个反中微子。类似于轻子,夸克也分成了3代:

它们都是弱同位旋群的2重态。
1960年代末,物理学家建立了电磁力和弱核力统一理论。弱电统一理论必须计及4种传递相互作用的玻色子:W±、Z和光子。这导致了规范群的选取,从简单性出发,最简单选择是SU(2)群加上U(1)群,所以弱电规范群就是SU(2)×U(1)。
二、标准模型
3个电子永远不会结合成一个束缚态,但是强相互作用能轻而易举地将3个夸克结合起来。夸克之间的强力是用胶子来传递的,夸克和胶子都带有电荷。色群是色空间中所有数学变换构成的对称群SU(3),数学家称之为3维特殊幺正群。对于非专业人士而言,这是一种行列式为1的,3×3矩阵组成的群。
用数学语言讲,夸克是色群的3维基本表示;用物理语言讲,夸克分成红、绿、蓝3色,当然这并非是光学上的三原色,而是3种色量子数。反夸克是3*维表示,带有反红、反绿和反蓝3种颜色。胶子是色群的8维伴随表示,每种胶子可带有一正一反两种不同颜色,如红反蓝、蓝反绿、绿反红等8种。组合3个各带不同色的夸克,就产生一个色中性的粒子。换句话说,红、绿、蓝3色合在一起就变成了无色,这与光学里看到的一样,色动力学的颜色类比就是由此而来。从上述讨论中也能看到,夸克和胶子的相互作用能改变夸克的颜色,例如一个红夸克发射出红反蓝的胶子,就会变成一个蓝夸克。
耗时半个世纪、耗费以百亿美元计的经费,人类在亚原子物质方面所取得的成就是:所有物质都由夸克和轻子组成,它们通过3种不同类型的玻色子传递相互作用,这些玻色子是胶子,弱玻色子和光子由SU(3)×SU(2)×U(1)规范场来描写。这样一种图景就称为粒子物理的标准模型。
在2021年4月7日颁布的µ子磁矩实验之前,标准模型几乎能够解释所有亚原子粒子的实验,许多人由此而认为它是物理学史上最成功的理论。他们还认为,物理学家毋庸再理会隐藏在深处的哲学思辨,只要应用现有的物理定律,去埋头制造各种芯片、激光器和计算设备,博得政治家在内的各个阶层的齐声喝彩。
三、石破天惊
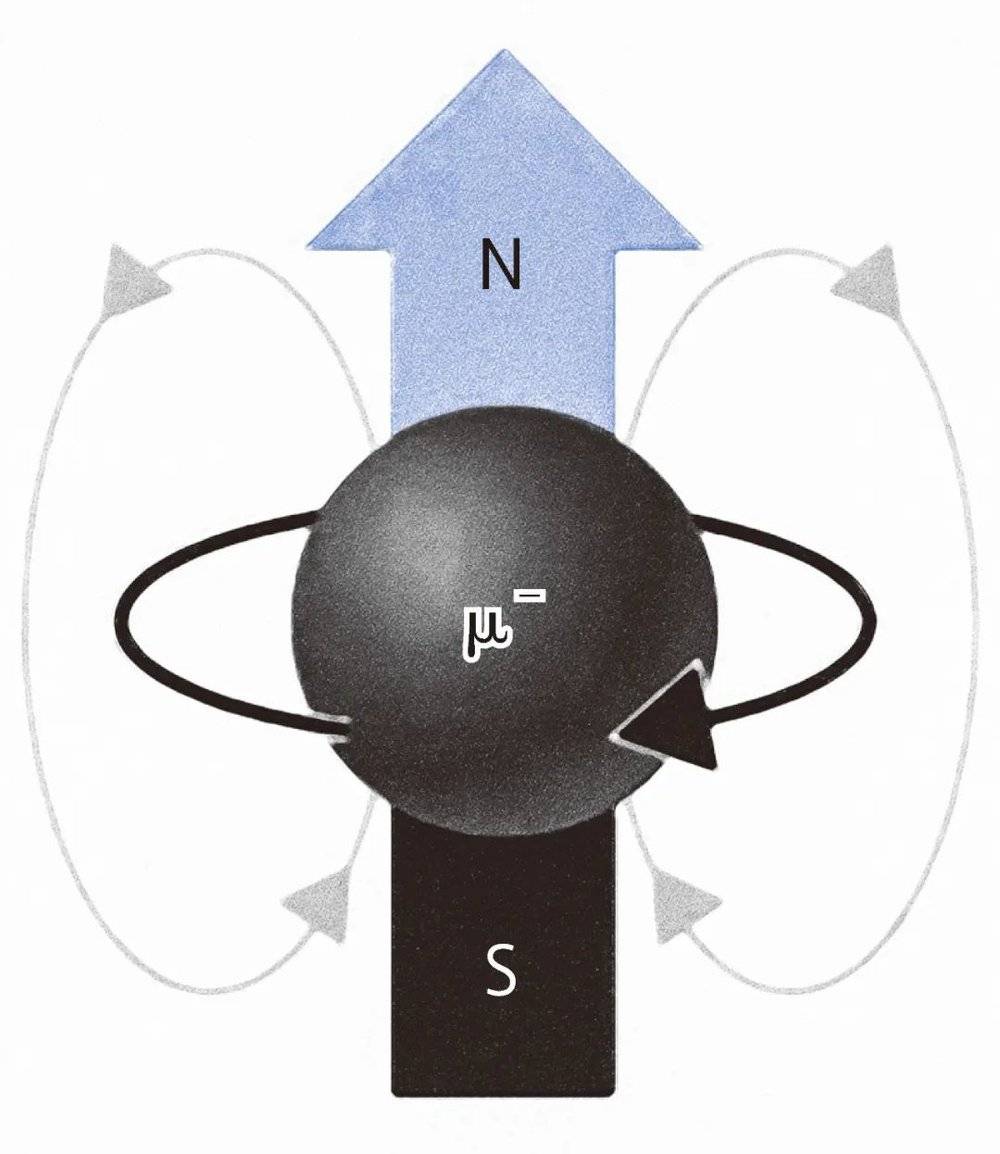
µ子的自旋为1/2,µ子带单位负电荷,所以µ子有点像一只带电的陀螺。一只匀速自转的带电陀螺,就会像一条磁铁一样,而这条“磁铁”的南北极在外磁场中会受到力的作用,这个力的大小与它自己的磁场大小相关。陀螺带的电荷愈多,或者转动得愈快,都会导致环形电流愈强,也就是磁场愈强。所以,一只带电陀螺在外磁场中产生的磁矩正比于陀螺的带电量和自转角动量。
倘若µ子处在磁场中,它的自旋轴就会绕着磁场旋转,类似于一只倾斜的带电陀螺绕垂直方向旋转。物理上称这类运动为进动。µ子在磁场中的进动率,由µ子的磁矩来表征。费米实验室测量µ子磁矩的原理很简单,将自旋轴倾斜于磁场方向的µ子,放进一个均匀的外磁场中,测量µ子转一圈后的自旋轴与原来的偏差,就能知道µ子的磁矩值了。
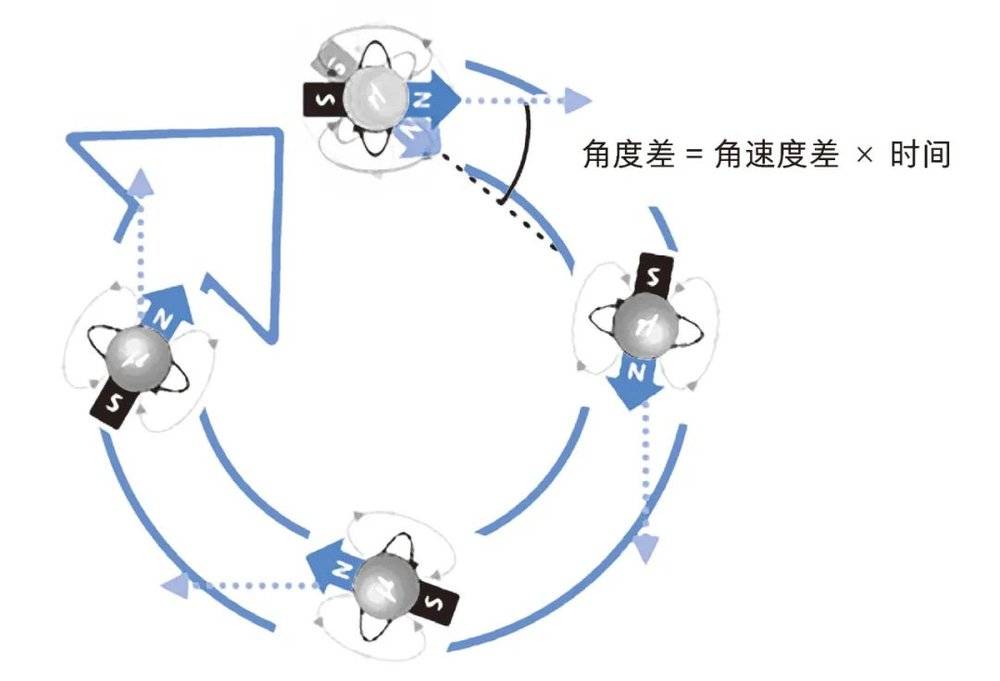
倘若读者略懂狄拉克方程,就能对µ子的磁矩作出粗略的估计,不过这样的估计精度只能达到千分之一。只有使用量子场论的方法,才能从理论上提高计算精度。根据量子场论,真空不空,虚粒子在极短的时间内不断产生和湮灭。由于这些虚粒子的寿命实在太短,无法直接用探测器来探测,但是它们却要对磁矩值做出贡献。
精确计算虚粒子的贡献,是件费时费力的工作,经过多年的努力,人们已能精确计算出这个值,称为µ子反常磁矩。对于参与强相互作用的粒子,迄今尚无办法作出精确计算,这也就是为什么在此类实验中青睐µ子的缘故。
费米实验室µ子g-2合作组宣布,他们将µ子磁矩测量值达到了史无前例的精确度——十亿分之一。就在这个精度上,发现了实验值和理论值的差异。用日常生活中的标准来看,这样的差异实在太小了。倘若你用一把米尺,从上海的石库门沿高速公路一直量到北京的天安门,测量的距离值要达到这个精度,误差就必须不超过2毫米。
但是,对于物理学家来说,这是一个石破天惊的结果。这是半个世纪以来,极为难得的机会,难道真实的物理世界和粒子标准模型描述的世界真的不一致?
四、路在何方
尽管尚未达到5σ的置信度,费米实验室的µ子磁矩实验也已达到了4.2σ,一石激起千层浪,究竟是要提高格点规范的计算精度,还是要提高实验的置信度?或者是超越粒子物理的标准模型?
众所周知,标准模型不美。它包含了大量的自由参数,不能用理论计算出来,反而需要实验测量后,作为对理论的输入。它们是6个轻子和6个夸克以及4个玻色子的质量;弱作用中用来控制夸克味混合的卡比博—小林—益川矩阵的3个角和相位;控制中微子味混合的庞蒂科夫—牧—中川—坂田矩阵的3个角和相位。最后,还要加上电磁和强两种相互作用的耦合强度,而弱作用的强度可用W,Z玻色子的质量与电磁耦合强度导出。简而言之,这15种质量、8个混合参数和2种耦合强度,给出了整整25个自由参数,标准模型不能给予诠释。
既然标准模型不美,现在又有了磁矩实验的引导,探索超越标准模型是件理所当然的事情。然而,摆在物理学家面前的是,路在何方?绝不是存在一种新的力的泛泛而谈就能解决问题的。我们并没有驶向成功彼岸的罗盘,我们手头的方案太多,而不是太少,可走的路成百上千,绝不是寥寥数条。
早在1978年那个科学春天,笔者就提出了一个修正标准模型的方案,发表在上海科学技术出版社的《自然杂志》创刊卷上。1992年,笔者又将这个方案纳入超弦框架中,发表在美国的《物理评论D》上。超弦是超越标准模型的一个严肃的候选者,它包含了描述低能物理的所有要素。然而,包括对标准模型做出重要贡献,1979年诺贝尔物理奖获得者格拉肖在内的众多物理学家,从认识论的角度反对弦论。
以往考虑的是一条自下而上的研究路径,用来探索新的基础物理学。超弦理论是一种自上而下的理论,与其说是从标准模型出发,不如说是构造比标准模型更为复杂的理论。弦论不知如何确定正确的低能模型的问题,被称为景观问题,这是一个认识论层面上的问题。
路在何方,也许应从超越标准模型的格点规范计算做起,计算出新的力对µ子磁矩的贡献,或者还要考虑超对称伙伴粒子的贡献。
路漫漫其修远兮,粒子物理学家将上下而求索,敢问路在何方,路就在脚下。
参考文献:
1. Abi B, et al. Measurement of the positive muon anomalous magnetic moment to 0.46 ppm. Phys. Rev. Lett. 2021, 126(14): 141801.
2. 顾鸣皋, 李新洲, 殷鹏程. SU(2)×U(1)×U'(1) 规范模型. 自然杂志, 1978(1): 274-276.
3. Li X Z, Zhang J Z. Superconducting strings from heterotic superstring. Phys. Rev. D, 1992, 45(8): 2888-2892.
4. 尼古拉斯·曼顿, 尼古拉斯·米. 后费曼物理学讲义. 李新洲, 等译. 上海: 上海科学技术出版社, 2021.
本文来自微信公众号:科学杂志1915(ID:kexuemag),作者:李新洲(上海师范大学天体物理中心教授)

