试想你有一个朋友,他对同一问题的回答会因你的提问方式不同而不同。
你问“秘鲁的首都是哪里?”他会给出一个答案;而问“利马是秘鲁的首都吗?”时,他却给出另一个答案。如此,你可能会有点担心你朋友的智力,不再轻易相信他给出的任何答案。
这种情况正发生在许多大语言模型(LLMs)上,这些强大的机器学习工具支撑着 ChatGPT及其它人工智能的运行。一个开放式的生成问题会得到一个答案,而涉及必须在选项之间进行选择的判别性问题,往往会得到另一个不同的答案。“同一个问题以不同的方式表达时,就会出现不一致。”麻省理工学院的博士生Athul Paul Jacob表示。[1]
为了让语言模型给出更加一致的答案,从而提高模型的整体可靠性,Jacob和他的同事设计了一个游戏,模型的两种模式被驱动寻找共同的答案。这个名为共识游戏的简单程序通过博弈论工具,提升了LLM的准确性和内部一致性。[2]

▷Jacob, Athul Paul, et al. "The consensus game: Language model generation via equilibrium search." arXiv preprint arXiv:2310.09139 (2023).
“针对这些模型内部一致性的研究非常有限,”机器人公司Field AI的首席科学官Shayegan Omidshafiei说。“这篇论文是第一批巧妙而系统地解决这个问题的论文之一,它为语言模型创建了一个可以自我博弈的游戏。”[3]
“这确实是一项非常激动人心的研究,”Google Research的研究科学家Ahmad Beirami说。他指出,多年来,语言模型对提示的响应方式一直没有变化。“麻省理工学院的研究团队通过引入游戏机制,为这一流程带来了全新的范式,可能会催生许多新的应用场景。”
一、将游戏融入研究
这项新的研究利用游戏来提升人工智能,与过去通过游戏来衡量人工智能成功与否的方式形成对比。
例如1997年,IBM的“深蓝”计算机击败了国际象棋大师Garry Kasparov,这标志着思维机器的一个里程碑。19年后,Google DeepMind的AlphaGo在对战前围棋冠军李世石的五局比赛中赢得四局,揭示了另一个人类不再称霸的竞技场。[4]此外,机器还在跳棋、双人扑克及其他零和游戏中超越了人类,这些游戏中一方的胜利必然意味着另一方的失败。
而对AI研究者来说,更大的挑战来自于“外交”游戏——这是像约翰·肯尼迪和亨利·基辛格这样的政治家所喜爱的。这款游戏不仅仅是两个对手,而是涉及七名玩家,他们的动机难以捉摸。为了获胜,玩家必须进行谈判,建立可以随时被违背的合作关系。外交游戏的复杂性极高,以至于当Meta一个团队编写的AI程序Cicero2022年在40场比赛中达到“人类水平”时也表示满意。虽未击败世界冠军,但该程序在对抗人类参与者中的表现足以排在前10%。
在该项目中,Meta团队的成员Jacob注意到Cicero依赖语言模型来与其他玩家进行对话。他意识到了尚未开发的潜能。他表示,团队的目标是“为这个游戏而构建的他们所能做到的最佳语言模型。”如果转而专注于创建能够最大化提升大型语言模型性能的游戏会怎样呢?
二、两厢情愿的互动
在2023年,Jacob在麻省理工学院继续探索他的研究课题,与Yikang Shen、Gabriele Farina和指导教授Jacob Andreas合作,开发了一种名为共识博弈的新模式。[5-7]这个游戏的核心概念是将两人之间的对话视作一种合作性游戏,其中成功的关键在于听者是否能理解说话者想要表达的内容。具体来说,共识博弈旨在调和语言模型中负责生成问题的生成器和处理判别问题的鉴别器两大系统。
经过数月的起起落落,团队最终将这一理念发展成完整的游戏。游戏开始时,生成器首先接收一个问题,这个问题可能来自人类或是预设的问题列表。例如:“巴拉克·奥巴马出生在哪里?”随后,生成器会收到几个可能的回答,如檀香山、芝加哥和内罗毕,这些答案可能来自人类、列表或是模型自身的搜索。
在给出回答前,生成器还需要根据一次公平的硬币抛掷,来决定其回答应正确还是错误。
如果硬币正面朝上,生成器则尝试给出正确答案,并将问题及其选定的答案发送给鉴别器。如果鉴别器认为生成器有意提供了正确答案,则双方各获得一分作为奖励。
如果硬币反面朝上,生成器则提供一个错误答案。若鉴别器判断该答案是有意提供的错误答案,他们再次各得一分。这样做的目的是为了鼓励双方达成一致。Jacob解释说:“这就像训练狗狗做动作,做对了就给予奖励。”
生成器和鉴别器在游戏开始时各自设定了一些“初始信念”,这些信念以概率分布的形式存在,关联到不同的选择。例如,基于从互联网上获取的信息,生成器可能认为奥巴马在檀香山出生的可能性为80%,在芝加哥的可能性为 10%,在内罗毕的可能性为5%,其他地方为 5%。
鉴别器可能会有不同的初始概率分布。尽管两名“玩家”通过达成一致来获得奖励,他们如果偏离最初的信念过远,也会受到惩罚。这种设置鼓励他们将对世界的认知——再次通过互联网获得——融入到他们的回答中,这能够提升模型的准确性。如果没有这种机制,他们可能会在一个完全错误的答案上达成一致,如德里,但仍然能够得分。
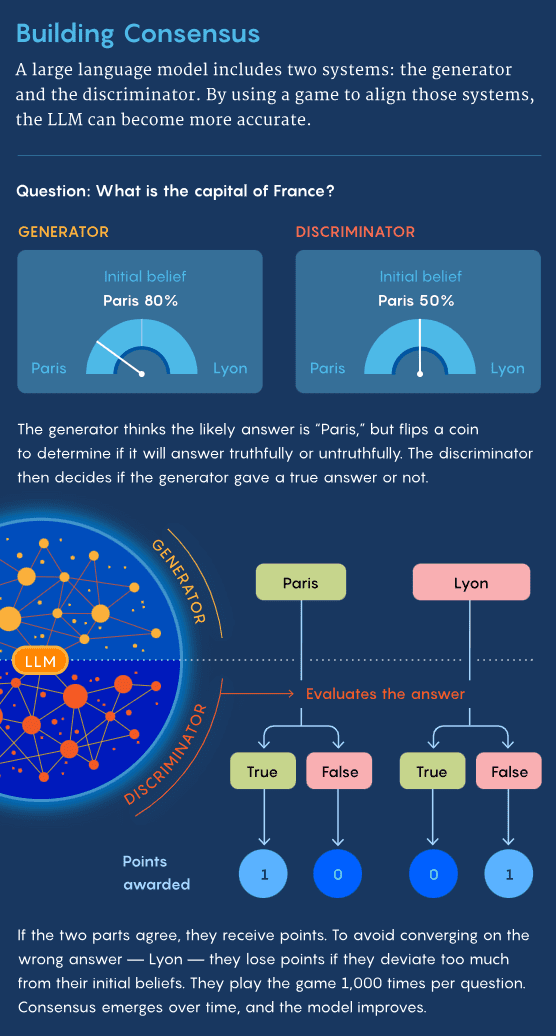
▷图源:Matt Chinworth
在每个问题上,这两个系统将进行大约1000轮的对决。通过这些重复的游戏,双方逐步了解对方的信念并调整自己的策略。
最终,生成器和鉴别器通过逐渐适应达到了所谓的纳什均衡。这是博弈论中的核心概念,它代表了游戏中的一种平衡状态,即任何玩家通过改变策略都无法改善自己的个人结果。例如,在石头、剪刀、布游戏中,当玩家均衡地选择每个选项时表现最佳,而任何其他策略都会导致更差的结果。
在共识博弈中,这种平衡可以通过多种方式体现。例如,鉴别器可能发现每次生成器发送“檀香山”作为奥巴马出生地时,它都能得分。经过反复的游戏,生成器和鉴别器将学会通过继续这样做来获取奖励,他们也没有动机去尝试其他任何事情。这种共识是针对这个问题可能的纳什均衡的众多示例之一。MIT团队还利用了一种修改版的纳什均衡,这种均衡考虑了玩家的先验信念,有助于确保他们的回答更加贴近现实。
研究人员观察到的总体效果是,参与这种游戏的语言模型变得更加准确,无论问题如何提出,都更可能给出一致的答案。为了测试共识游戏的效果,团队对几个参数在7亿到13亿之间的中等规模语言模型进行了一系列标准问题的测试。这些模型在正确回答的比例上常常超过了未参与游戏的模型,即使是那些参数高达 540亿的大型模型也是如此。参与游戏还提升了模型的内部一致性。
原则上,任何LLM都能从与自身进行游戏的过程中获益,而在标准笔记本电脑上进行的 1,000轮游戏仅需几毫秒。Omidshafiei指出:“这种方法的一个显著优点是它的计算需求非常低,不需要对基础语言模型进行训练或修改。”
三、用语言玩游戏
获得初步的成功之后,Jacob现在正探索其他将博弈论融入LLM研究的方式。初步的结果显示,通过与多个小型模型一同参与一个名为集成游戏的游戏,已经表现强大的LLM能够进一步提升性能。在这个游戏中,主要的LLM至少有一个小模型作为盟友,至少有一个扮演敌对角色。例如,当主要LLM被问及美国总统是谁时,如果其答案与盟友一致,则获得一分;如果答案与对手不同,也同样获得一分。这种与小型模型的互动不仅能提升LLM的性能,而且无需额外训练或更改参数即可实现。
这只是一个开始。Google DeepMind的研究科学家 Ian Gemp表示,由于许多情境都可以视为游戏,博弈论的工具可以在多种现实世界的情境中得到应用。在他与同事们于2024年2月发表的一篇论文中,他们研究了需要比简单问答更复杂交流的谈判场景。“这个项目的主要目标是让语言模型具备更多的策略性。”

▷Gemp, Ian, et al. "States as Strings as Strategies: Steering Language Models with Game-Theoretic Solvers." arXiv preprint arXiv:2402.01704 (2024).
他在一个学术会议上讨论的一个例子是期刊或会议的论文审查过程,尤其在最初提交被严厉批评后。鉴于语言模型能够为不同的回应分配概率,研究者可以构建类似于扑克游戏的游戏树,图示出可选的策略及其可能的结果。"做到这一点后,你就可以开始计算纳什均衡,并对各种反驳进行排序,"Gemp说。模型本质上是在指导你应该怎样回应。
得益于博弈论的洞察,语言模型未来能够处理更加复杂的互动,而不再仅限于问答问题。“未来的重大进展将关注更长的对话。”Andreas 说。“下一步是让人工智能与人而非仅与另一个语言模型进行交互。”
Jacob将DeepMind的工作视为共识博弈及集成游戏的补充。“从更高层次看,这两种方法都是在结合语言模型与博弈论。”他说,尽管各自的目标略有不同。虽然Gemp小组正通过游戏化常见场景来协助战略决策,Jacob表示,“我们正在利用我们对博弈论的了解来改进一般任务中的语言模型。”
Jacob表示,这些努力目前呈现为“同一棵树上的两个分支”——利用两种不同的方法来增强语言模型的功能。“我们希望在未来一到两年内,这两个分支能够得到融合。”
参考文献
[1]: https://apjacob.me/
[2]: https://openreview.net/forum?id=n9xeGcI4Yg
[3]: https://scholar.google.com/citations?user=nm5wMNUAAAAJ&hl=en
[4]: https://www.quantamagazine.org/tag/alphago/
[5]: https://mitibmwatsonailab.mit.edu/people/yikang-shen/
[6]: https://www.mit.edu/~gfarina/about/
[7]: https://www.mit.edu/~jda/
本文来自微信公众号:追问nextquestion (ID:gh_2414d982daee),作者:Steve Nadis,编译:丹雀,审校&编辑:张心雨桐

