在系列的前两篇文章中,主要介绍了强化学习的基础概念:《图解强化学习——基础概念 1》《图解强化学习——基础概念 2》。
本文是《图解强化学习》系列的第三篇文章,主要介绍强化学习流行的解决方案,对这些方案进行分类,并着重阐述了贝尔曼方程。
贝尔曼方法是所有强化学习算法的基础,从贝尔曼方程出发,更容易理解后续各种强化学习算法的原理。
一、RL 问题解决方案分类
我们已经知道,解决一个 RL 问题即是找到最优策略(Optimal Policy)或最优值(Optimal Value)。找到 Optimal Policy 有许多算法,这些算法可以根据不同的原理和应用场景进行分类。
1. 通过“基于模型的 VS 无模型“进行分类:
广义上讲,寻找最优策略的算法可以分为两大类:
基于模型的解决方案——Model-based approaches
无模型的解决方案——Model-free approaches
Model-based 方法适用于已知环境内部运行情况的场景。换句话说,当从某个当前状态开始执行某个操作时,我们可以准确判断,环境给出的下一个状态(Next State)和奖励(Raward)是怎样的。
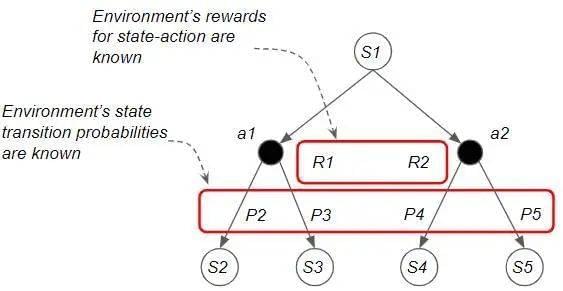
Model-free 方法适用于环境非常复杂,且其内部动态不为人知的情况。这种方法将环境视为一个“黑盒”,不尝试去理解里面的具体运作机制,而是直接观察输入和输出间的关系。
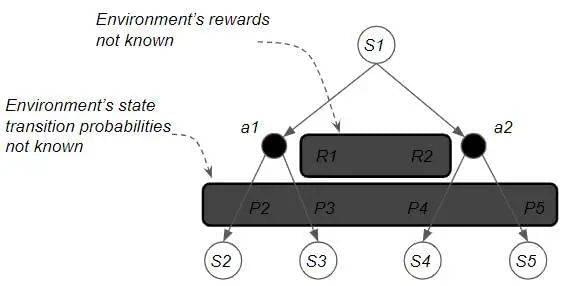
2. 通过”预测 VS 控制“进行分类
另一种较高维度的区分方法是通过预测(Prediction)和控制(Control)。
预测问题-Prediction problem:在这类问题中,我们的目标是给定一个策略,预测使用此策略能得到的累积回报,也即价值函数。此处的策略可以是任何策略,并不限于最优策略。
控制问题-Control problem:控制问题不提前给定策略,而是通过不断尝试与探索,在所有可能策略中找到能够获得最大回报的最优策略。
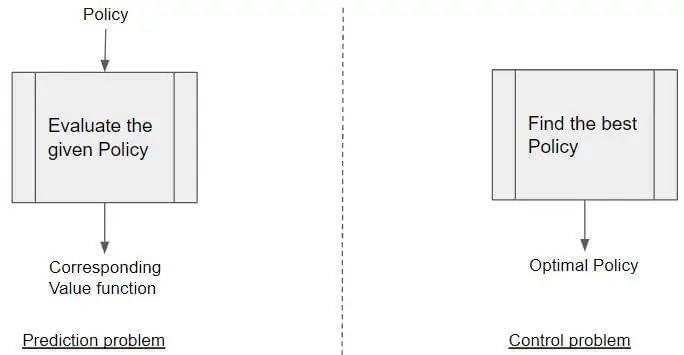
大多数实际问题都是 Control problems,因为我们的目标是找到最优策略 Optimal Policy。
3. RL 算法分类
根据以上的分类方法,常见的 RL 算法分类如下:
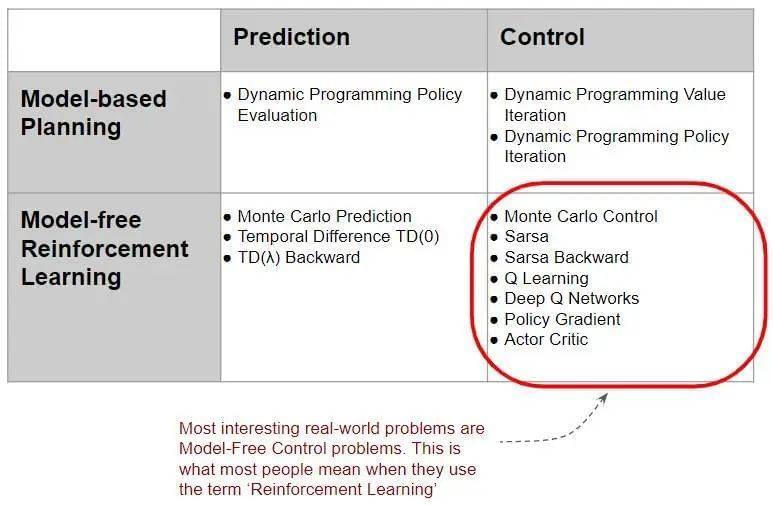
现实世界中,大部分的 RL 问题都属于 Model-free 的控制问题。因此,本系列内容将主要聚焦于这一类问题,对基于模型的解决方案只做简略讨论。
二、Model-based Approaches(基于模型的方法)
基于模型的方法可以得出每个状态和行动交互的精确结果,因此可以通过分析找到解决方案,而无需与环境进行实际交互。例如,在使用基于模型的方法下棋时,你需要将所有棋局的规则和策略编码在程序中。
与之相对,无模型算法对棋局规则一无所知,它通过观察动作和获得的奖励来抽象地学习游戏。
由于现实环境的复杂性,构建一个完整的模型往往是不可行的,这就是为什么大多数现实问题采用Model-free的方法。
三、Model-free Approache(无模型方法)
Model-free 方法依赖于与环境的直接互动来学习。这种方法不预设环境的内部机制,而是通过一系列的试错,观察每一次动作后环境的反馈(状态变化和奖励),从而学习如何在这个环境中取得最佳表现。
1. 与环境互动
在 Model-free 的学习过程中,由于环境的内部机制对我们来说是不可见的,算法必须通过直接互动来“观察”环境的行为。
算法扮演 Agent 的角色,每执行一个动作,就记录下其后环境的反应(即下一个状态和相应的奖励),并根据这些信息不断调整策略,是一个持续学习与适应过程。
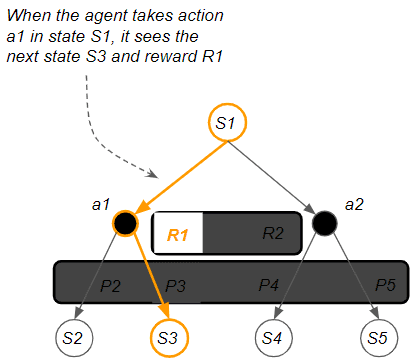
这一学习过程,类似于人类通过尝试和错误获得经验一样,算法通过执行动作并根据反馈(正面或负面)来逐步调整其行为。
2. 互动的轨迹即为 Agent 的 training data
在与环境互动时,Agent 每个时间步的动作都构成了一条特定的路径,即所谓的“轨迹”。
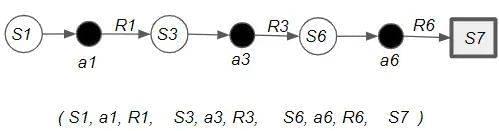
Agent 的轨迹就形成了算法学习和训练的基础数据。
四、Bellman方程:强化学习的数学基础
在了解用于解决 RL 问题的算法之前,我们需要学习一点数学知识,以便更准确地理解这些概念。
Bellman方程基于一个简单而直观的数学关系,是所有强化学习算法的核心。虽然这个方程有不同的变形,但它们都源于一个共同的基本概念。通过逐步解析,我们可以更好地理解这一概念。
1. 从终止状态回溯Work back from a Terminal State
考虑这样一个场景:Agent 从某一状态出发,只采取了一个行动,就到达了终止状态。
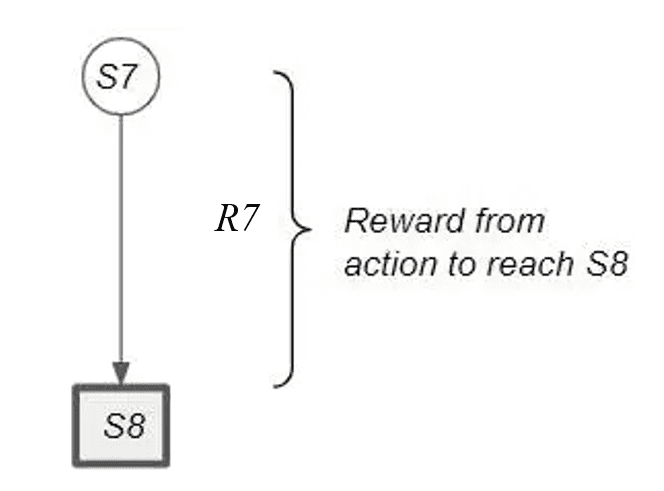
这种情况下,该状态下的回报与采取该行动获得的奖励相同。即:G7 = R7。
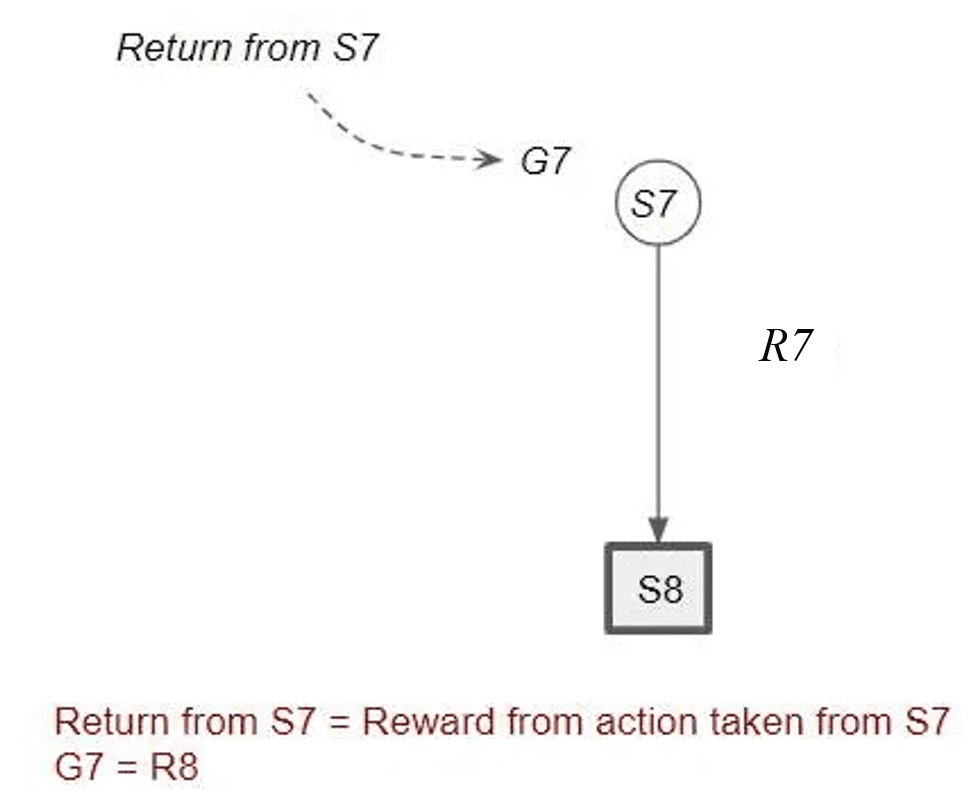
现在考虑之前的状态 S6。S6 的回报 =为达到 S7 采取行动获得的奖励+从 G7 到达终止状态的折扣回报。即:G6 = R6+γR7 = R6+γG7。
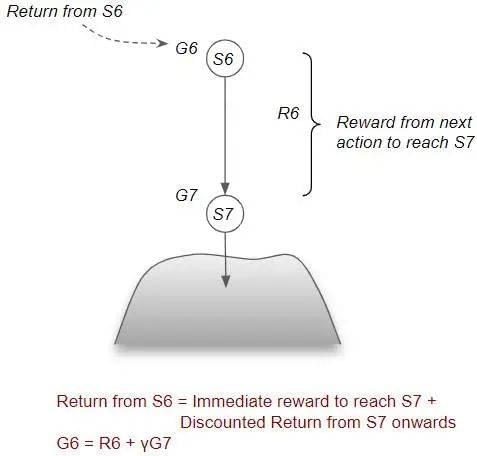
2. 回报的 Bellman 收益方程
总体上,任何状态的回报都可以被拆解为两个部分:一是从当前状态到下一个状态的即时奖励;二是从下一个状态开始,按照特定策略行动,未来的折扣回报。这种递归关系被称为 Bellman 方程。
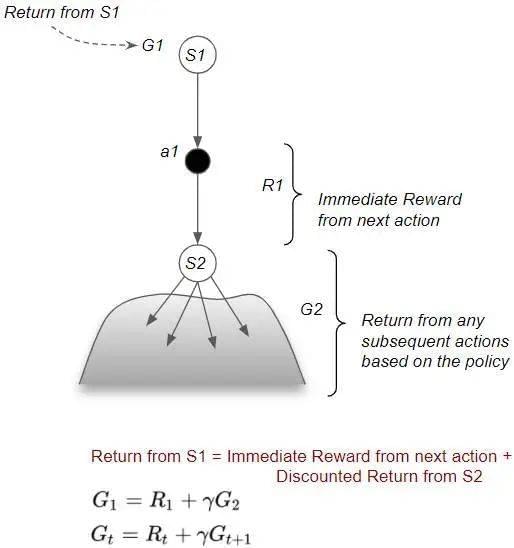
3. 状态价值函数的 Bellman 方程
如果说“回报”关注的是单一路径上的累积奖励,那么“状态价值(State Value)”则是考虑了在多条路径上,平均情况下的预期回报。换言之,状态价值综合考量了从某状态出发,采取各种可能动作所能获得的回报的平均水平。
因此,状态价值(State Value)同样可以被分解为两部分:一部分是从当前状态出发,执行下一个动作所获得的即时奖励;另一部分是考虑时间折扣后的,从下一状态继续遵循策略所能带来的价值。
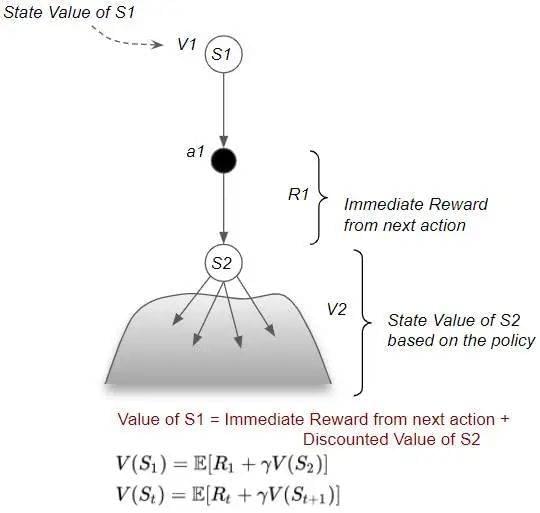
3. 状态-动作对价值函数的贝尔曼期望方程
同样,“状态-动作价值(State-Action Value)”也可分解为两部分:达到下一状态的行动所带来的即时奖励,以及在所有后续步骤中遵循该策略所获得的下一状态的折扣价值。
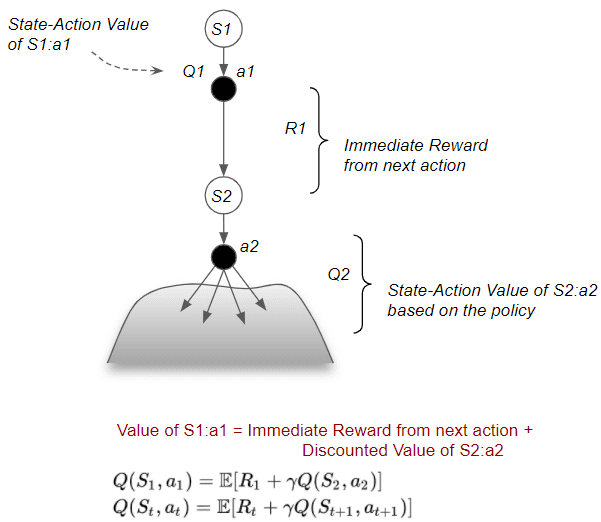
五、Bellman方程为什么有用?
从贝尔曼方程中,我们可以得出两个重要结论。
1. 递归计算回报
第一点,为了计算回报,我们不必走完一个回合。一个回合可能很长,或遍历成本很高,也可能永无止境。我们可以利用这种递归关系。如果知道下一步的回报,就可以使用它。在 RL 过程中,只需要迈出第一步,观察到这一步的回报,然后使用后续时间步的回报,而无需遍历之后的整个回合。
2. 基于估算而非精确值
第二点,涉及计算同一目标的两种方法:一种方法是基于当前状态直接计算的回报(Return);另一种方法是将单步的奖励(reward)与下一状态的回报相加。
要直接测量从某个状态开始直至整个回合结束的实际回报,计算代价很高,我们通常采用回报的估计值。通过这两种不同的方法来计算这些估计值,并通过对比两个结果来验证估计的准确性。
考虑到这些仅是估计值而非精确值,两种计算方法得出的结果可能会有所不同。这即是估计中的误差。误差可以帮助我们改进估算结果,以减少误差的方式修正估算结果。
请牢记这两个概念,因为所有强化学习算法都会用到它们。
总结
现在,我们对强化学习(RL)问题及其解决方案有了初步认识,是时候深入探讨解决这些问题所采用的技术了。鉴于在实际问题中最常采用的是 model-free 方法,我们将聚焦于此。这将是下一篇文章的讨论焦点。
本文来自微信公众号:Afunby的 AI Lab(ID:AI_Lab_of_Afunby),作者:Afunby

