出于众所周知的原因,《科学美国人》说《为什么说大模型永远不会停止幻觉?》。如果你还不知道这些原因,请参阅笔者对于大模型幻觉产生机理的分析文章《GPT4技术原理五:大模型的幻觉,解铃还须系铃人》。
如果你是技术背景,而且一直跟踪笔者整理的大模型的数理认知思维框架,到这里,就很可能会产生如下疑问:所有环节似乎都是在做最优化,为何结果却不准确了呢?大模型的所谓创意还会有用吗?
要回答这个问题,笔者觉得需要先从两个视角看清大模型的认知机理:范畴视角下的Transformer, 和Transformer视角下的范畴。
一、范畴的必要概念
然而范畴理论是一门抽象到天际的数学理论。对于接受过常规数学教育的人来说,极易与现有数学知识体系混淆,难以理解和驾驭。笔者觉得,范畴论适合在高等数学概念还是一张白纸的时候学习。
大体可以如此理解,尽管不严谨:范畴理论是研究关系的学问,研究对象就是事物之间的关系,关系(也是一种事物)的关系,关系的关系(更高阶的事物)的关系。
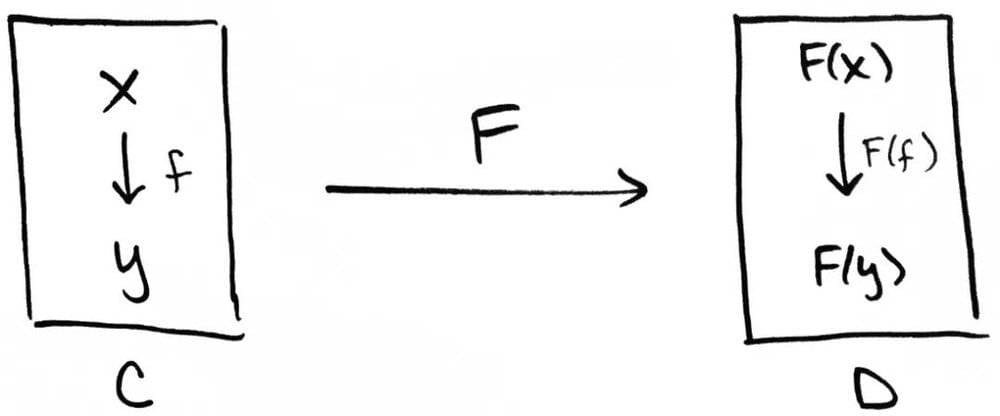
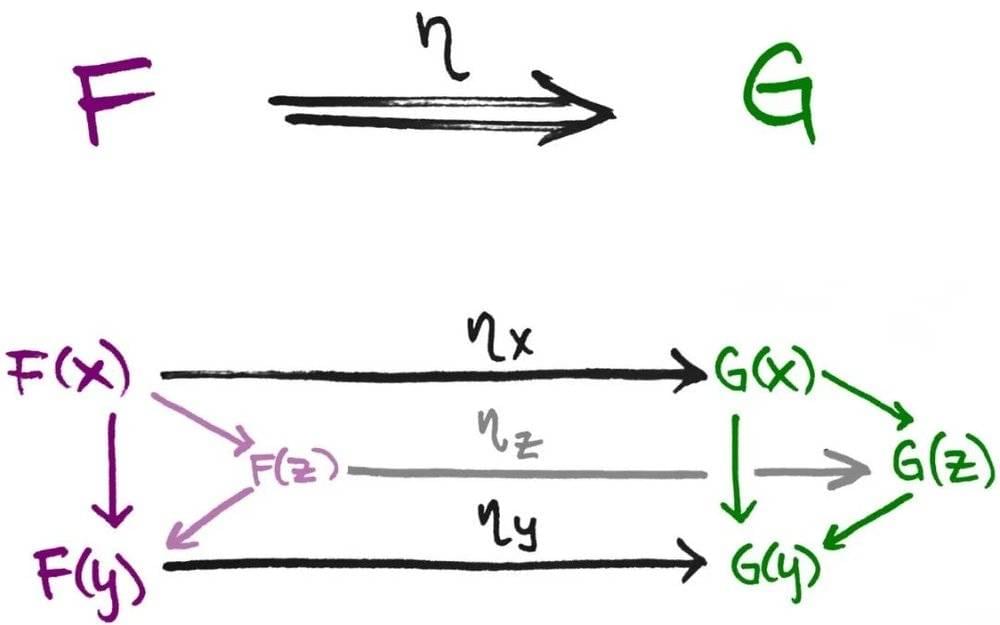
高等数学背景还能如此类比理解范畴中的晦涩概念:
态射(morphism)是范畴内对象间的某种运算;
函子( functor )就是范畴间的函数,可以映射范畴中的对象和态射;
自然变换(natural transformation)可以类比为泛函,函数与函数间的映射。
分别对应范畴学里面讲的1、2、3阶范畴。
二、范畴视角下的Transformer
《Transformer网络的范畴 The Topos of Transformer Networks》(文献1),提供了对Transformer神经网络的范畴学阐释。

学者们声称从topos(中文译为拓扑斯,笔者觉得翻译得很怪异,可以简单理解为一类特殊的范畴)的角度对神经网络架构做了理论分析,注意到前馈Feed Forward网络架构和Transformer神经网络架构之间的以前未知的差异。一类属于pretopos,另一类则是topos completion。
这种区别使得topos completion中的架构与反向传播和架构搜索关联起来,在单一设计空间中编码许多已知的神经网络架构。优点是:多种不同的架构系列可等同,差异影响架构类的表达性,由架构中的逻辑片段来定义。关键结论如下:
第一,自注意力机制可以分解为对网络参数的选择choose和对神经网络的评估eval。

第二,分段线性函数PL构成pretopos,ΣPL 是PL 的cocompletion,Para(PL)是PL的参数化范畴,可以发现,存在函子将ΣPL中的choose态射,map 到对参数空间和范畴态射的选择,以对神经网络进行再参数化。

通俗地讲,通过预训练,找到组合分段线性函数的方式,逐层不同,就是Transformer在范畴视角下的工作机制。作者通过范畴的方式找到了Transformer 神经网络单层的本质,但是笔者觉得作者有意或者无意忽视了归一化和逐层的跨尺度重整化。
论文作者的视角与相应的结论,让人们不难看出,神经网络与传统的一些依赖核函数的机器学习算法,如高斯过程,或者支持向量机,并无本质不同。甚至跟有限元的思想也有几分神似,差别在有限元的核函数是已知的物理方程,而神经网络则是choose适合的分段线性核函数,并参数化。
万法归宗,以前笔者分析过,所有AI问题,最终都归结到概率分布距离计算和优化的问题,即 wasserstain 距离将一统天下。由此篇进一步得出,所有神经网络架构都是一个核函数选择和参数化的过程,区别是人工选择还是机器选择,选择的是PL, 还是sin, cos, 抑或是小波基函数。
三、Transformer视角下的范畴
不幸的是,我们希望用神经网络处理的问题,都是极其复杂的、具备极高自由度或者说极高维度的问题。这是宇宙对于人类智能的维度诅咒。随着维度的增加,会有许多反直觉现象,这带来高维空间信息处理的重大限制。
除了类似有限元等方法,对于已知物理方程的场景,人工选择核函数通常是天方夜谭;通过预训练来选择,则面临海量的数据处理效能的问题。
但高维度可增强线性可分性,使核函数方法更加有效,而我们的神经网络架构特别擅长从高维空间中选择和提取复杂模式。这里存在一种权衡:利用好这些优势,同时平衡增加的计算量与模型效能的潜在收益。
维度灾难的克星是尺度重整化。不要挑战重整化理论的数学严谨性,人类科学认知的一切其实都是近似的。大模型都是提纯知识,而不是压缩知识,比如伯克利马毅教授的信息论视角。
重整化本质是尺度从小到大,粗粒度化概率分布的过程,而深度神经网络擅长从学习小尺度结构逐级到认知全局特征,而大模型的Transformer 则可以逆重整化流,逐尺度重建微观概率分布,从而完成生成。
在范畴的相变与知识的形成一文中,笔者总结了大模型认知框架的三个关键环节:1. 重整化从海量语料中提取出范畴;2. 持续重整化驱动范畴解构重组以至相变;3. 生成过程是于范畴中采样做变分推理。
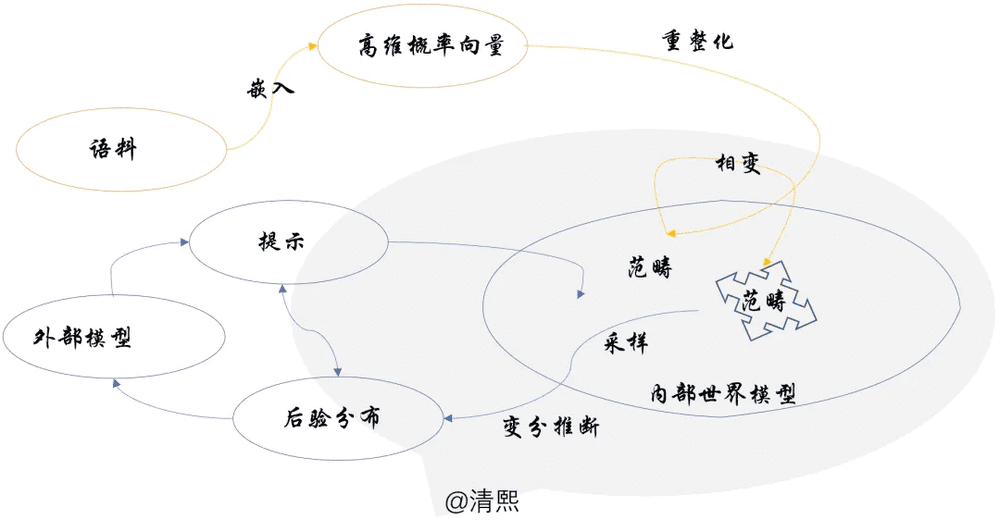
这里的范畴是Transformer视角下的高维概率向量编织起来的事物之间的各种复杂的关系,从海量的预训练数据集中提纯出来,对大量的分段线性核函数参数化后的表达。这些关系,关系的关系,关系的关系的关系,本质上,在范畴论概念下,就是对事物的米田嵌入。
米田嵌入,某种意义上是将范畴C中对象“编码”到范畴 SetCop 。注意Cop与C中对象相同,但是态射都是反向的。米田嵌入其实是米田编码表征,即采用该对象的所有关系来表征该对象。范畴学上称为,X 与 hom(-,X)同态或同构。
Transformer 学习的过程,是核函数选择与参数化的过程,也是寻找米田嵌入的过程:提取object 的所有关系,形成其关系图像,注意这里存在相变。
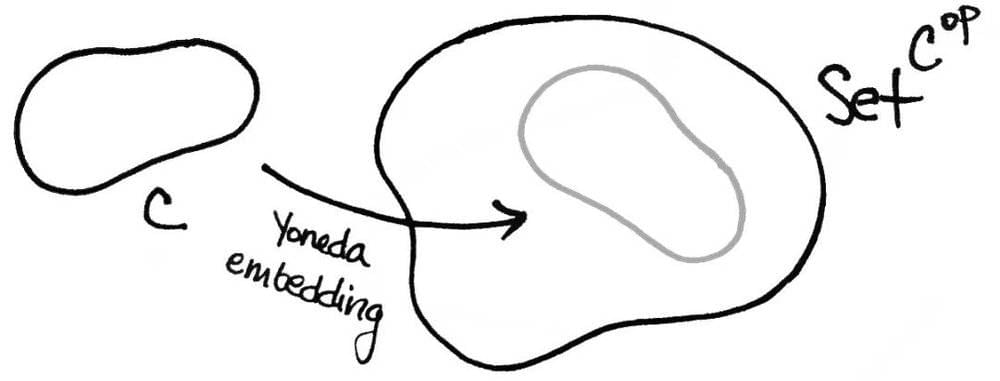
这就是大模型学习了各种范畴关系之后的可怕之处,毕竟范畴就是关系,关系的关系,关系的关系的关系,而海量训练语料中的各种对象,都被米田嵌入到了大模型学习的范畴中。所以大模型的所谓创意将会非常有用。
然而,我们体验到的大模型输出却常常含有似是而非的幻觉,导致其在严谨的企业数据分析领域的应用步履蹒跚。如供应链物流路径优化,传统的运筹学明显比Transformer更擅长。如何消除或者至少是降低大模型的幻觉呢?
四、优化基于范畴的采样降低幻觉
关于大模型的幻觉,解铃还须系铃人,笔者倾向于从LLM内部解决现有问题的思路,这里有三个关键点:
Self-awareness,非自我意识,而是加强LLM对学到的范畴的结构和关系的理解;
范畴内和跨范畴采样改进,依据更好的“范畴的结构和关系的理解”优化采样算法;
构建内部工作空间,管理短中长期多层次记忆与范畴交互,推理规划与使用工具。
这不同于RAG等从外部修正大模型输入输出以降低幻觉的方式。以下是笔者读到的最新的两个工作,都可以归为从内部解决幻觉问题的思路,特别是改进提升“范畴内和跨范畴采样,依据更好的‘范畴的结构和关系的理解’优化采样算法”。
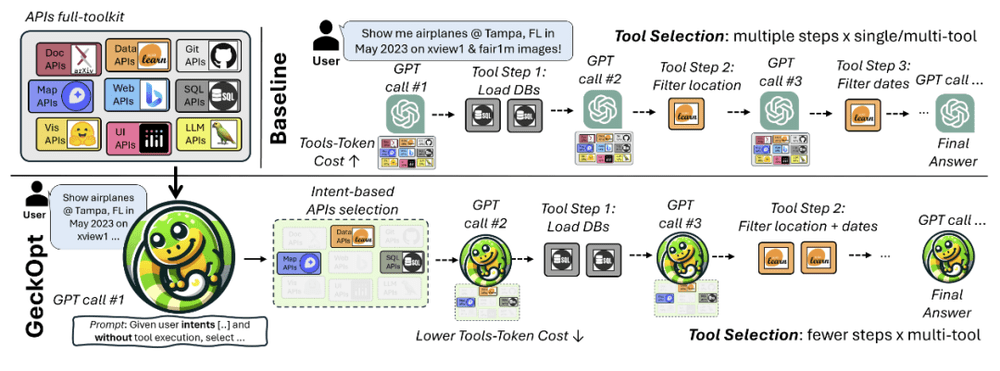
1. GeckOpt:通过基于意图的工具选择,提高 LLM 系统效率
微软学者开发的 GeckOpt 系统引入了一种基于意图的工具选择的尖端方法(文献2)。这种方法通过前置的用户意图分析,在任务开始执行之前优化 API 工具的选择。简化 LLM 操作方面的成功,为广泛采用基于意图的工具选择方法提供了强有力的案例。通过有效降低操作负载和优化工具使用,该系统降低了成本并增强了 LLM 应用程序跨不同平台的可扩展性。
本质上是,基于对“范畴的结构和关系的理解”,对“潜在工具”范畴采样,缩小到与“任务特定要求最相关”的工具,从而实现“生成”优化:最大限度地减少不必要的API调用,并将计算能力集中在最需要的地方。
2. 具有因果图约束的神经网络: 一种新的治疗效果估计方法
巴塞罗那大学的学者探索了使用机器学习技术来估计治疗效果这一核心领域(文献3)。通过分析当前依赖于表征的学习策略,提出了一种新模型NN-CGC:通过实施新的约束来解决由虚假变量相互作用产生的偏差,在治疗效果估计方面取得了该领域最领先的结果SOTA。
作者认为表征学习策略忽略了一个特定的偏差来源:模型中变量之间的虚假相互作用,也就是神经网络从海量语料中学习到的,实际上没有因果关系的变量之间的“伪”关系。这些虚假的交互作用关系,可能被作为相关捷径,扭曲估计的因果效应,特别是在数据有限的情况下。
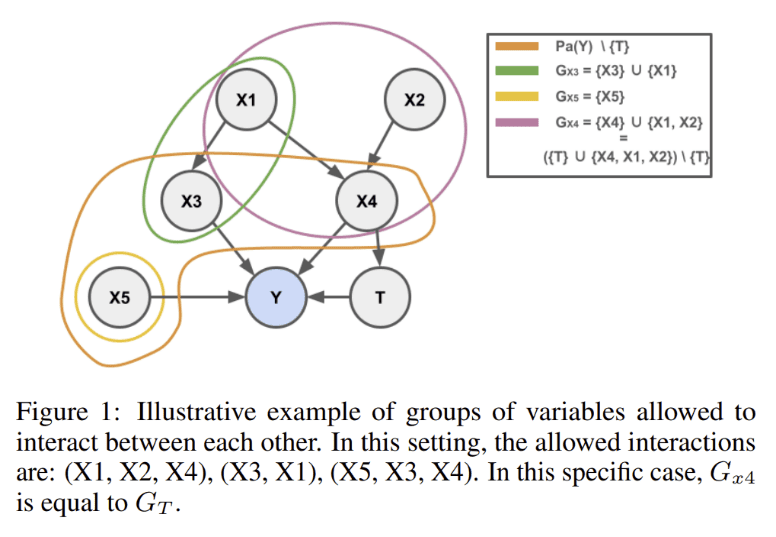
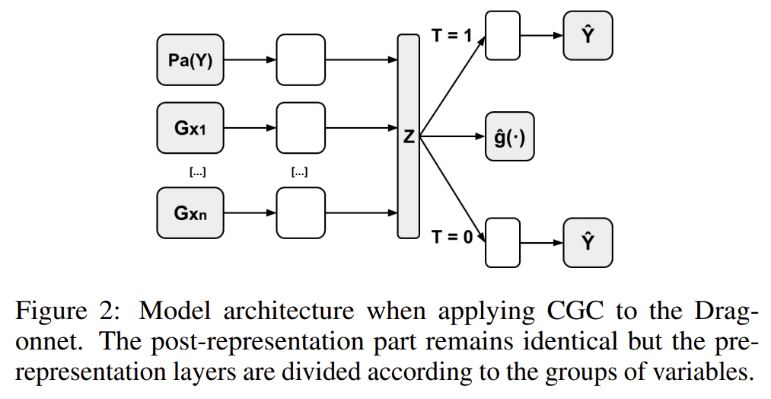
NN-CGC背后的核心思想是约束神经网络的学习分布,也就是限定了于范畴内或范畴之间采样的方式,使其更好地与因果模型保持一致,从而有效地减少对虚假交互的依赖。其工作原理可以简述为:
根据因果图(或专业知识),将输入变量划分为组。每个组都包含彼此因果相关的变量。每个变量组通过一组层单独处理,对结果变量及其直接原因的独立因果机制进行建模。通过单独处理每个变量组,NN-CGC 确保学习的表征不受来自不同组的变量之间的虚假交互的影响。独立组表示的输出被组合并通过线性层传递,形成最终表征。
五、写在最后
“今天的 LLM 从来都不是为了纯粹准确而设计的。它们被创造出来是为了创造。没有办法保证所生成内容的真实性,所有创造力在某种程度上都是幻觉”。因而笔者一直强调现阶段大模型应用场景选择的一个最重要原则:创意大于准确性。
但是大模型技术日新月异地发展,即使大模型永远不会停止幻觉, 在未来,专业系统也会验证LLM输出,为特定环境优化的人工智能工具将部分取代今天的通用模型。其中最重要的改进方向就在于,通过引导大模型学习人类特定的先验,更好地理解“范畴的结构和关系”,优化范畴内和跨范畴采样算法,将幻觉降低到“不可见”范围,尽管很难消除为零。
参考文献:
文献1:https://arxiv.org/pdf/2403.18415.pdf
文献2:https://arxiv.org/abs/2404.15804
文献3:https://arxiv.org/abs/2404.12238
本文来自微信公众号:清熙(ID:qingxitech),作者:王庆法

