本文来自微信公众号:新智元 (ID:AI_era),编辑:编辑部,原文标题:《陶哲轩攻克60年几何学难题!发现“周期性密铺猜想”在高维空间反例》,题图来自:视觉中国
几何学中的“周期性密铺猜想”,被陶哲轩推翻了。
几年前,数学家证明了,无论你想出的密铺多么复杂或巧妙,如果只能对单个密铺使用平移,那么就不可能设计出一个只能非周期性地覆盖整个平面的密铺。
数学家们推测,这样结果也适用于高维空间。这个假设被称为周期性密铺猜想。

但现在,陶哲轩等人通过构造了一个可以非周期地填充高维空间,但不能周期性地填充高维空间的密铺,推翻了这个猜想。

什么是周期性密铺猜想?
密铺问题,可以说是几何学中最古老,也是最经典的问题。
所谓“密铺”,即是指平面图形的镶嵌。换句话说,就是用形状、大小完全相同的平面图形进行拼接,使彼此之间不留空隙、不重叠地铺成一片。
在密铺问题中,用正方形、三角形或六边形去覆盖一片空间很容易。
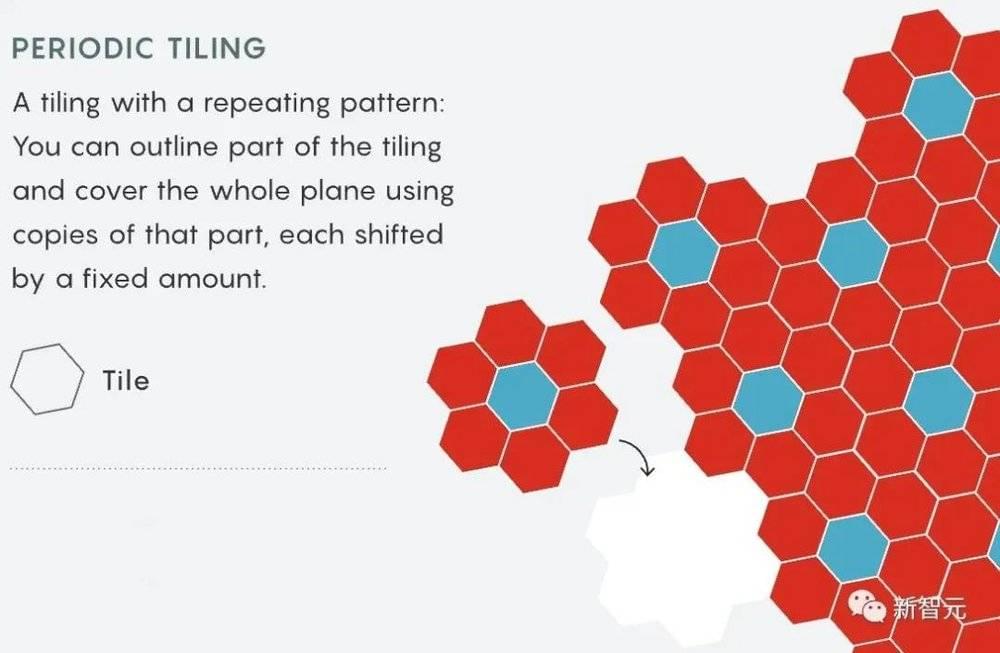
但是,在1960年代,数学家Robert Berger发现了一组有趣的密铺,它们可以完全覆盖平面,但只能以永不重复的方式覆盖。
作为第一组非周期性密铺,它由20426个平面图形组成。当然,Berger很快将其减少到104个。在此之后,数学家们的努力方向就是:降低这个数字。
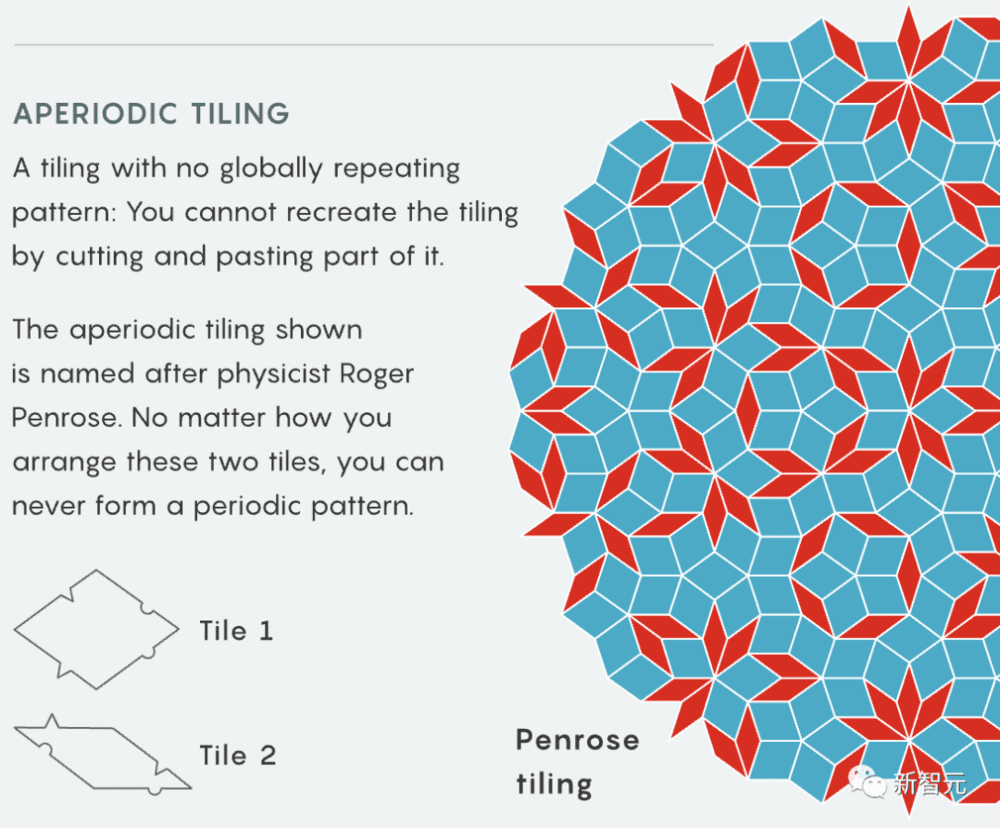
如今,最著名的就是Penrose在20世纪70年代发现的非周期性密铺,它只用两种图形就能覆盖一个平面:风筝和飞镖。
如何想出不重复的密铺呢?这并不难。通过调整许多重复的周期性密铺,都可以做到。比如,在一个形如棋盘排列的无限方格中,我们对每一行都进行移动,使其与上面一行有明显的偏移。
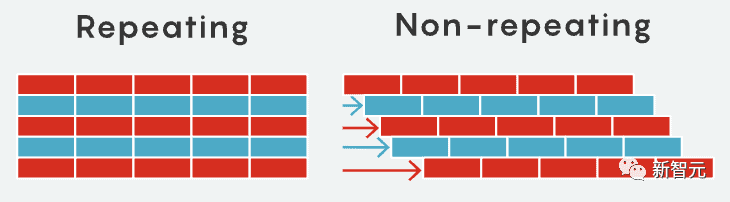
诀窍就在于,找到一组可以覆盖整个平面的镶嵌,只不过是用不重复的方式进行。
既然Penrose已经把密铺图形数量降到了两块,那么,有没有可能,有这么一块形状巧妙的图形,也可以组成密铺?
答案是肯定的,但前提是你可以对图形进行旋转和颠倒。
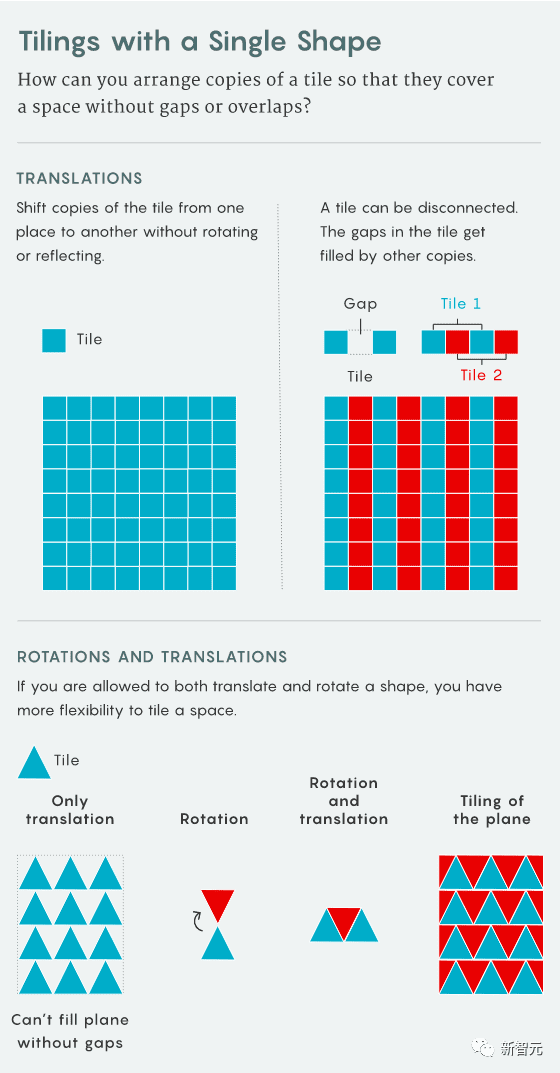
但如果规定:不允许旋转图形,那就不可能不留空隙。
在几年前,数学家Siddhartha Bhattacharya就证明了,无论我们想出多么复杂、多么微妙的密铺图形,但如果规定,只能使用单个密铺的位移或平移,那么就不可能设计出一个只能非周期性地覆盖整个平面的密铺。
也就是说,如果对一个形状在填充空间时施加足够的限制,就可以迫使一个周期性的模式出现。

论文地址:https://arxiv.org/abs/1602.05738
数学家推测,Bhattacharya的二维结果也适用于高维空间。
他们猜测:正如不存在非周期性二维图形一样,也不存在合适的三维(或更复杂)的图形,同理可以推广到任意大的维度之中。
这个假设被称为周期性密铺(periodic tiling)猜想。
这个猜想,被陶哲轩等人打破
但是他们错了。在上个月发布的预印本中,陶哲轩和Rachel Greenfeld一同最终推翻了这个猜想。

不同的是,他们用的却不是数学家们通常预期的方式。他们的方式是:构建了一个可以非周期性填充高维空间,但不能周期性填充的密铺。
而对此,有其他数学家推断:他们的结论,在所有维度上,或许都是正确的。
数学家Mihalis Kolountzakis说:“这真是一个惊喜,我希望这个猜想在所有维度上都是正确的。不过,在足够高的维度上,只凭直觉的话,恐怕不会走得太远。”
陶哲轩等人的工作,不仅突破了几何上可能和不可能的界限,甚至还延申到了几何以外的问题——逻辑本身的极限。
2019年,Rachel Greenfeld以博士后研究员的身份,来到加州大学洛杉矶分校。

此前,陶哲轩和她都一直在独立研究另一个与平移密铺(translational tilings)相关的问题。随后,两人将目光投向了周期性密铺猜想。
此前,这个猜想在一维和二维中已经为人所知,而他们试图在三维上证明这个猜想——如果可以移动某个形状的三维版本来密铺整个三维空间,那么,一定有一种方法,可以周期性地密铺整个三维空间。

陶哲轩和Rachel Greenfeld取得了一些进展,通过一些技巧,他们在二维中重新证明了这个猜想。
然而,当他们希望把同样的技巧应用于三维空间时,却碰壁了。
陶哲轩说:“在某些时候,我们感到很沮丧,所以不得不这样想:好吧,也许我们无法在更高维度上证明这个猜想,是有原因的。我们应该开始寻找反例。”

他们开始着手梳理所有非周期性领域的文献。
他们从历史上第一个文献开始——1964年出版的20,000多块密铺的集合,可以通过位移(translation)覆盖平面,但只是非周期性的。
从这里,他们开始着手新的技巧,来构建单个非周期性的密铺。

他们的思路是:改变环境。
如果想密铺一个二维空间,那么,与其尝试密铺一个连续平面,不如考虑密铺一个二维网格——也就是一个排列在网格中的无限点阵列。
可以将密铺定义为,该网格上的一组有限点。如果有一个合适的密铺,那么就可以通过复制有限的点集,并将它们四处滑动,来精确覆盖网格中的每个点。
证明高维网格的“离散”周期性密铺猜想,与证明这个猜想的连续版本略有不同,因为有些密铺在格子中是可能的,但在连续空间中是不可能的。
但是,这两个猜想是相关的。陶哲轩和Greenfeld希望提出一个离散的反例,随后再修改这个证明,让它适用于连续的情况。
在2021年夏天,他们终于逼近了目标——在一个超高维空间中,他们找到了两块密铺。
这两块密铺,可以填充它们所在的空间,但不是周期性的。

“这还不够”,Greenfeld说。“二者非常接近,但两块密铺比一块密铺更不牢固,刚性要差得多。”
他们还需要一年半的时间,才能为周期性密铺猜想,构建出一个真正的反例。
密铺三明治
他们从创建一种新语言开始——把要解决的问题,以一种特殊的方程式重写出来。
他们需要解决的,就是这个方程式中的未知“变量”,它们代表了密铺高维空间的所有可能方式。
“但是,其实你很难用一个方程式来描述事物。”陶哲轩说。“有时,你需要多个方程,来描述一个非常复杂的空间集合。”
因此,陶哲轩和Greenfeld重新构建了他们试图解决的问题。
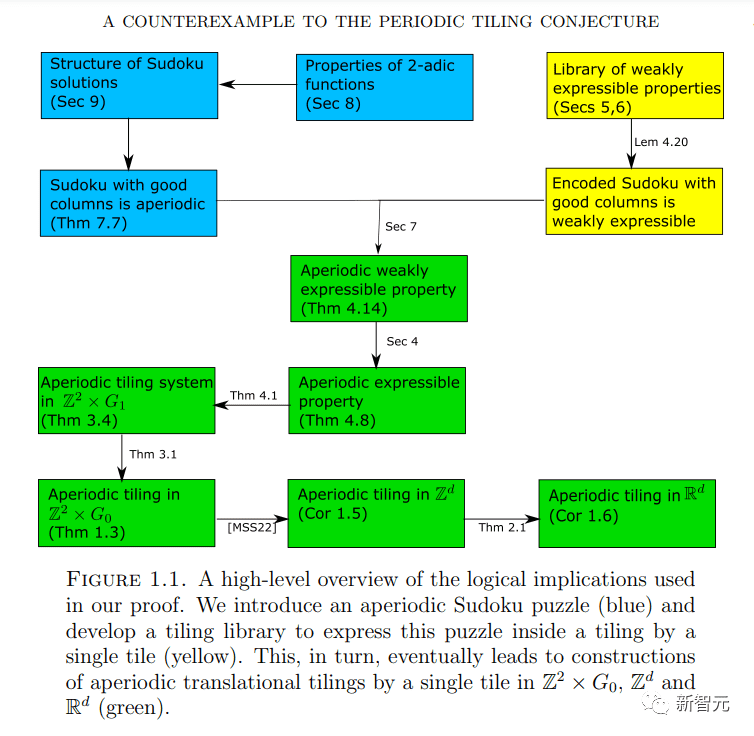
他们意识到,可以改为设计一个方程组,其中每个方程都会对其解编码有不同的约束。
这样,他们就可以将问题分解为一个关于许多不同密铺的问题——在这个例子中,所有密铺都使用同一组位移(translation)覆盖给定空间。
例如,在二维空间中,可以通过向上、向下、向左或向右滑动一个正方形来密铺平面,一次一个单位。
但是其他形状也可以使用完全相同的一组位移来密铺平面:例如,一个正方形的右边缘添加了一个凸起,左边缘被移除,就像拼图一样。
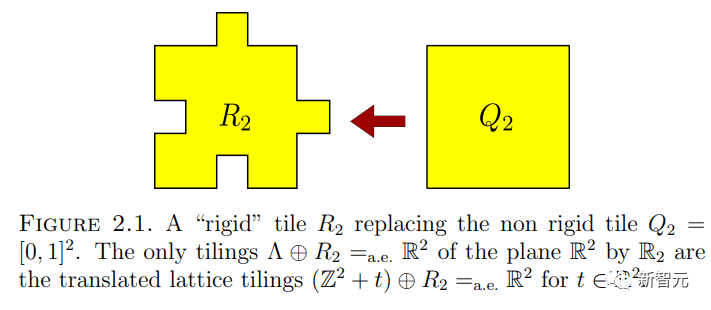
如果我们用一个正方形、一块拼图和其他使用同一组位移的图块,像三明治中的冷切一样,将它们堆叠在一起,就可以构建出一个使用单组平移覆盖三维的图块空间。
而陶哲轩和Greenfeld,需要在更多维度上做到这一点。
“因为无论如何,我们都是在高维度上工作,所以增加一个维度,对我们也没有什么坏的影响。”陶哲轩说。
相反,增加一个维度,为他们提供了额外的灵活性。

他们试图扭转这种三明治的构建过程,将单方程、高维密铺问题,重写为一系列较低维度的密铺方程。这些方程式,就决定了之后的高维密铺结构的样子。
就如之前陶哲轩所说:“只要你有两块密铺,它们就可以组合成非常复杂的东西。”
陶哲轩和Greenfeld将方程式系统视为计算机程序:每一行代码或方程式都是一个命令,这些命令组合起来,就可以生成实现特定目标的程序。
陶哲轩表示:“逻辑电路是由非常基本的对象组成的,这些与门和或门,单看都不是很有趣。”
“但你可以将它们堆叠在一起,制作出一个可以绘制正弦波,或者在互联网上通信的电路。”
“所以,我们开始将这个问题,视为一种编程问题。”
每个命令,都是他们的最终密铺需要满足的不同属性,因此,整个程序需要保证,符合所有标准的任何密铺,必须是非周期性的。
这样,问题就变成了:在所有密铺方程中,需要编码什么样的属性,才能实现这一点?
例如,三明治的一层中的一块密铺的形状,可能只允许某些类型的运动。
陶哲轩和Greenfeld必须仔细地建立约束列表——这样它就不会严格到排除任何解决方案,但是足以给出足够的限制,来排除所有周期性的解决方案。
“游戏的关键是,要构建正确的约束级别,以编码正确的谜题。”Greenfeld说。
无限数独
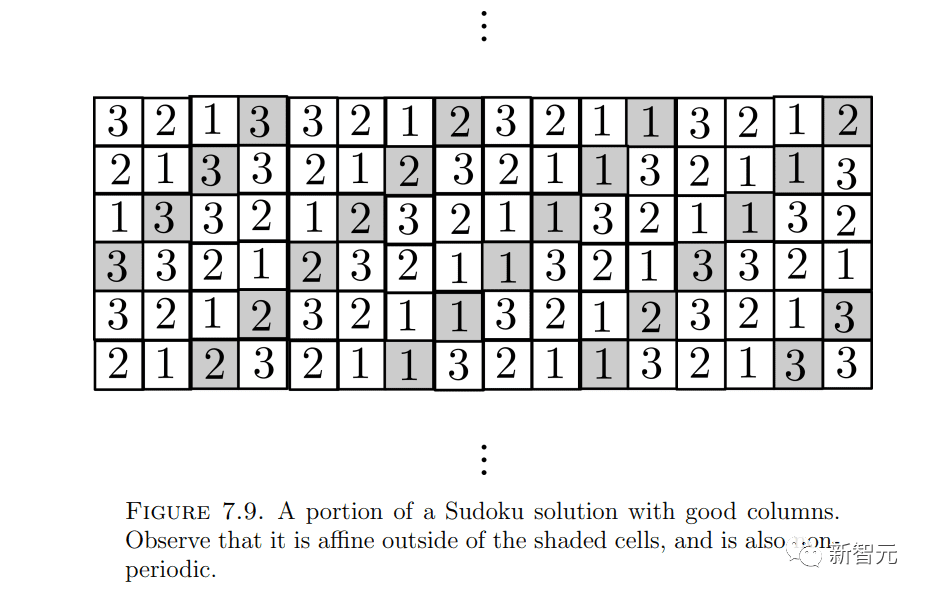
陶哲轩和Greenfeld希望,用他们的密铺方程编程的拼图,是一个具有无限行数和大量和有限列的网格。
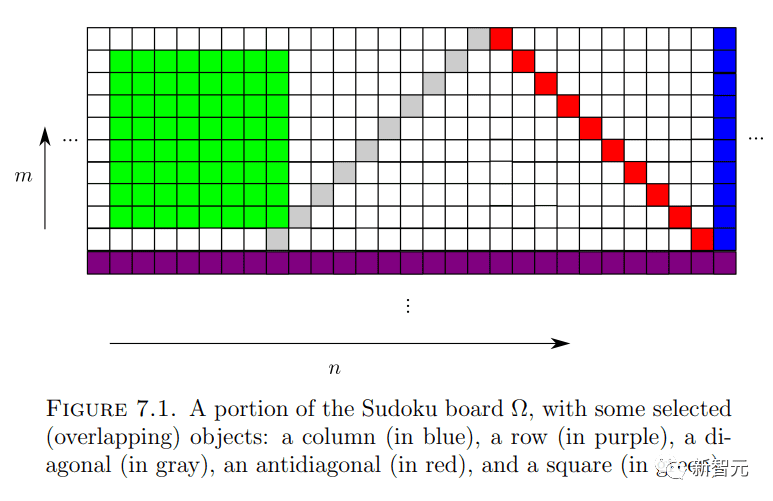
对两人来说,这是一个巨大的数独谜题:用特定的数字序列填充拼图的每一行和对角线,这些数字序列对应于他们可以用密铺方程描述的各种限制。
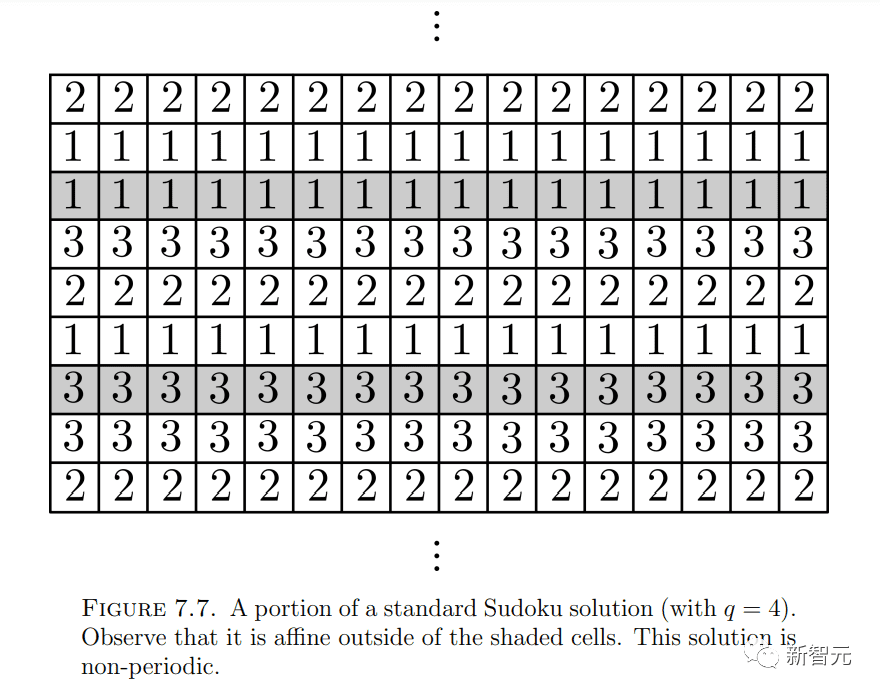
然后,两人发现了非周期性的序列——这意味着相关密铺方程组的解也是非周期性的。
“这个谜题基本上只有一个解。有趣的是,这是一个概周期解(almost periodic)。”陶哲轩说。“我们花了很长时间才发现这一点。”
英属哥伦比亚大学的数学家Izabella Łaba说:“概周期函数并非数学中的新概念,但这确实是概周期函数的创新用法。”

正如Iosevich所说,陶哲轩和Greenfeld“创造了一个基础物体,并将其抬高到一个极其复杂的境界”。
根据概周期函数,陶哲轩和Greenfeld在离散场景和连续场景中构建了一个高维非周期性平面图形。
设计的平面图形十分复杂,充满曲折和孔洞,以至于几乎没有密铺空间。
陶哲轩和Greenfeld没有计算它所居住的空间的维度。他们只知道它很大,大约有2的100次方的100次方(或者3后面跟199个零)那么大!

“我们的证明是建设性的,所以一切都是明确的和可计算的。”Greenfeld说。“但是因为它离最佳状态非常非常远,所以我们并没有进行验证。”
二人认为可以在更低维度找到非周期性平面图形,这是因为她们的建构中,一些更具技术性的部分需要在概念上“非常接近二维”的空间中完成。
她不认为他们会找到一个三维平面图形,但她说四维图形可能存在。因此,Iosevich说,他们不仅反驳了周期性密铺猜想,还“以最打脸的方式做到了这一点。”
下一步:尝试不完备理论
陶哲轩和Greenfeld的研究,为构建非周期性密铺提供了新方法,二人认为该方法可以用于反驳其他密铺相关的猜想。
这项工作不仅触及了人类直觉,还涉及数学推理的边界。
上世纪30年代,数学家库尔特·哥德尔(Kurt Gödel)提出了著名的哥德尔不完备理论。

哥德尔提出,自然数系统内“自洽性”和“完备性”不可兼得:有些命题在该系统中既不能被证明也不能被证伪。只能放弃一个,保全另一个,有点鱼和熊掌不可兼得的意思。
同样,数学有许多计算上不可解的问题,即任何算法在有限的时间内都无法解决的问题。
数学家在1960年代发现,关于密铺的问题也可能是不可解的。
也就是说,对于某些图形集,人们可以证明在有限的时间内,不可能弄清楚它们是否能完成密铺。

“这是一个非常简单的问题,但仍然超出了数学的范围。”耶鲁大学数学家Richard Kenyon说。“这不是第一个出现某种数学理论不可解或不完备的例子,但它确实是最接地气的理论。”
去年,陶哲轩和Greenfeld发现,关于高维密铺对的一般命题是不可解的:他们证明了没有人能够确定平面图形是否可以实现密铺(无论是周期性的还是非周期性的)。
关于单个平面图形的命题是否也是不可解的呢?
自1960年代以来,人们就知道,如果周期性密铺猜想成立,那么人们可以确定任何给定的图形是否能实现密铺。
但反之则不一定如此。仅仅因为存在非周期性的图形,并不意味着该问题不可解。
这就是陶哲轩和Greenfeld接下来想要弄清楚的问题。
陶哲轩说:“我们认为,我们创造的语言应该能够创造一个无法确定的难题,这是非常合理的。因此,可能有一些密铺,我们永远无法证明它是密铺空间或非密铺空间。”
为了证明一个命题不可解,数学家通常会证明它等同于另一个已知不可解的命题。
因此,如果这个密铺问题也被证明是不可解的,那么它可以作为证明其他命题的参考工具——这个意义远远超出了密铺的范畴。
与此同时,陶哲轩和Greenfeld的结果在某种程度上是对科研人员的提醒。
“数学家喜欢简洁大气的命题”,Iosevich说,“但遗憾的是,并不是所有有趣的数学命题都能做到这一点。更多时候,需要我们的研究才能出现期待的效果。”
参考资料
https://www.quantamagazine.org/nasty-geometry-breaks-decades-old-tiling-conjecture-20221215/
https://terrytao.wordpress.com/2022/09/19/a-counterexample-to-the-periodic-tiling-conjecture/
https://baike.baidu.com/item/%E5%AF%86%E9%93%BA/5106336
本文来自微信公众号:新智元 (ID:AI_era)

