本文来自微信公众号:墨子沙龙(ID:MiciusSalon),作者:Sheldon,绘制:赏鉴、周源,原文标题:《漫画 | 量子计算优越性+2up:我国团队同时升级了两种量子计算原型机》,头图来自:视觉中国
假设我们正在玩“扔硬币”的游戏。请你猜一猜,我扔出正面的概率是多少?
你肯定会说,太简单了!连小学生都知道,一枚硬币扔出正面的概率是50%——如果其中没有什么猫腻的话。
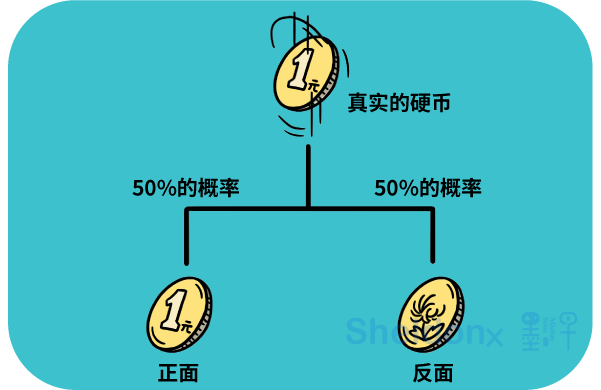
现在,我换个难度提问:假如我们扔的不是普通硬币,而是一枚量子硬币呢?
这个时候,你可能就原地愣住了,问:“量子硬币是个什么东西呢?”
一、量子比特:一种量子的硬币
世界上任何一台量子计算装置中,都包含一种量子的硬币。这种量子硬币有一个我们熟知的名字,叫量子比特。



量子比特,是量子计算机操纵的基本数据单元。跟经典计算机中的经典比特类似,我们通常用0和1来表示它的两种输出。
但跟经典计算机中的经典比特有所不同,一个量子比特不仅可以等于0(或等于1),它还可以处于一系列“同时处于0和1”的量子叠加状态。
那么,为什么我们可以把量子比特看作一种量子硬币呢?
这是因为,当一个量子比特处于某个“同时处于0和1”的量子叠加状态中时,如果你要从量子计算机中读取它时,它并不是直接输出这个叠加状态给你看,而是会立刻改变原先的量子叠加状态,并随机地变成“等于0”或“等于1”的状态,并输出给你看。
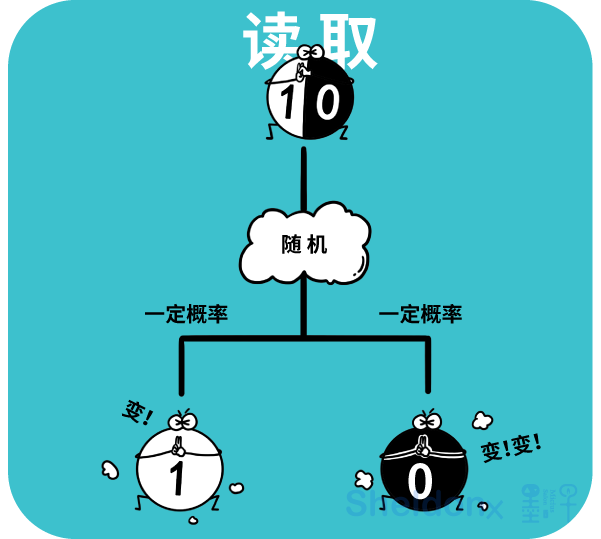
也就是说,读取一个量子比特的过程,就像你在扔一枚量子硬币,完全是随机发生的。

同时,读取一个量子比特的结果,也像你在扔一枚量子硬币,结果要么是1(如同硬币的正面),要么是0(如同硬币的反面),绝对不会存在其他结果。

如此看来,量子比特真的可以看成某种基于量子力学原理的硬币。

好了,了解了量子比特就是一种量子硬币,我们再回到刚才的问题:假如我们扔出一枚量子硬币,它正面朝上的概率是多少呢?
二、概率的概率分布:量子硬币的输出
对于这个问题,物理学家的回答是,这要看量子比特具体处于何种量子状态。
一枚普通硬币,只要随机地扔出去,出现正面和出现反面的概率一定各占50%。
但对于量子硬币(量子比特)来说,情况就不一样了。
处于某种特殊量子状态的量子硬币,不管你怎么扔,它出现正面的概率都是100%。
处于另一种特殊量子状态的量子硬币,不管你怎么扔,它出现正面的概率都是0。
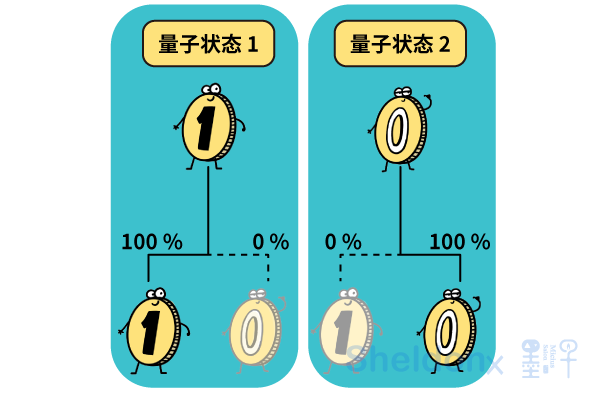
同理,处于各种量子叠加状态的量子硬币,不管你怎么扔,它出现正面的概率都是固定不变的,我们记作x;同时,它出现反面的概率也是固定不变的,等于100% - x。只不过,对于某些量子叠加状态而言,x = 10%;对于另一些量子叠加状态而言,x = 13.6%;……总之,根据所处量子状态的不同,x可以在0到1之间任意取值。

所以,要想知道量子硬币扔出以后的概率,我们就得预先知道这枚量子硬币处于以上哪种情况。用物理学的黑话来说,我们得预先知道这个量子比特处于哪一种量子状态。
可是,如果我死活不告诉你这枚量子硬币属于以上哪种情况呢?或者说,我们根本不知道这个量子比特处于哪一种量子状态呢?

这时,物理学家能给出的唯一合理答案是,以上情况皆有可能,每种情况的出现都对应一定的概率。如果“把正面朝上的概率大小”画成一张概率分布图,那么你就会看到一张这样的图:
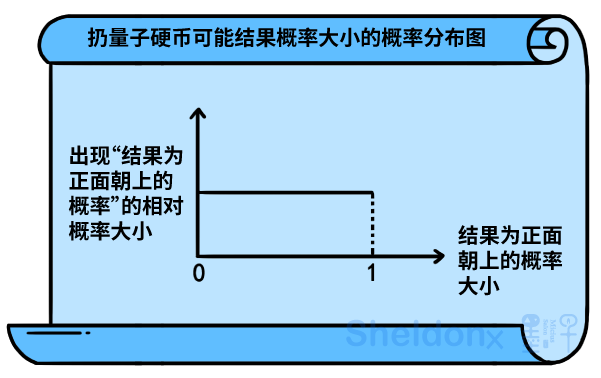
把这张图翻译成大白话就是:
我们有1%的概率得到一枚处于特定量子状态的量子硬币,将它“扔出正面朝上的概率为0-1%”;我们有1%的概率得到另一枚处于不同特定量子状态的量子硬币,将它“扔出正面朝上的概率为1%-2%”;……我们有1%的概率得到又一枚处于不同特定量子状态的量子硬币,将它“扔出正面朝上的概率为99%-100%”。

这就是物理学家对这个问题能给出的最好回答。
为什么这个回答这么绕呢?因为量子力学算出来就是这个结果。由于计算过程涉及一定数学知识,我就不具体讨论了。

反正你只需要知道,假如我扔出一枚量子硬币,问它正面朝上的概率是多少。正确的答案不是一个具体的概率值,而是一张关于概率大小的概率分布图,就可以了。
现在,我又要提高难度了:假如我们扔的不是一枚量子硬币,而是一枚具有2N个面的多面量子骰子呢?

三、体现量子计算优越性:扔出2N个面的多面量子骰子
说到这儿你可能有点儿不耐烦了?我们好不容易搞清楚了一枚具有正反面的量子硬币怎么扔,现在为啥突然要去研究具有2N个面的多面量子骰子呢?
这是因为,这个问题涉及量子计算的优越性。
我们经常听物理学家夸量子计算,说量子计算千好百好,就是好呀就是好!那么量子计算到底好在哪儿呢?
用一句话概括量子计算的好处,就是:
量子计算在计算某些特定问题时,比经典计算高效得多!相比量子计算,世界上最高级的经典计算机在处理这些问题时,效率跟水熊虫跑马拉松、蜗牛拉中欧班列、树懒爬珠穆朗玛峰差不多。

这就叫量子计算的优越性。

于是问题又来了,量子计算在处理哪些特定问题时,能够切实体现量子计算的优越性呢?
其中一个问题,就是我们刚才说的,扔一枚具有2N个面的多面量子骰子。
跟扔量子硬币不同,扔一枚具有2N个面的多面量子骰子,我们得到的不是正面朝上或反面朝上两种结果,而是会得到1号面朝上、2号面朝上……2N号面朝上,共2N个不同的结果。这些结果分别对应N个量子比特输出“000...0”(N个0)、输出“000...1”(N-1个0和1个1)……输出“111...1”(N个1),共2N个不同的结果。

跟扔量子硬币类似,对于一枚特定的多面量子骰子,它1号面朝上、2号面朝上……2N号面朝上的结果出现的概率都是固定不变的。这些概率的具体数值取决于扔骰子时,骰子对应何种量子状态。
同样,跟扔量子硬币类似,多面量子骰子本身可以处于各种不同的量子状态。如果两个多面量子骰子所处的量子状态不同,它们扔出各种结果的概率也往往会各不相同。
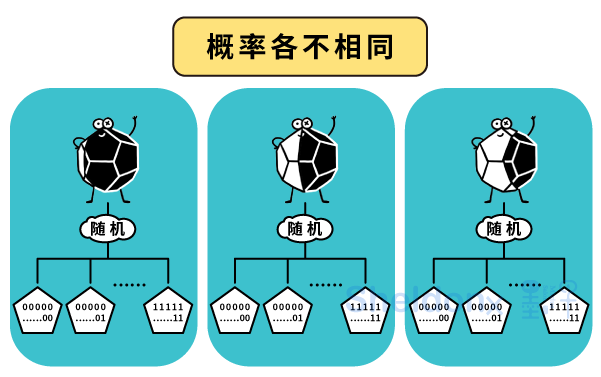
最后,仍然跟扔量子硬币类似。如果我问,扔一枚多面量子骰子,得到1号面朝上、2号面朝上、……2N号面朝上的结果出现的概率分别是多少?
你只能回答:我们有a%的概率得到一枚处于特定量子状态的多面量子骰子,它1号面朝上、2号面朝上、……2N号面朝上的结果出现的概率分别是a1%, a2%, a3%……
我们有b%的概率得到一枚处于另一种特定量子状态的多面量子骰子,它1号面朝上、2号面朝上、……2N号面朝上的结果出现的概率分别是b1%, b2%, b3%……
………
这个问题回答起来实在是太麻烦了。所以,为了简单起见,我们把最终所有可能的结果画成一张概率分布图:

这张图的意思是说,不管是1号面还是2号面还是3号面朝上,我们把所有结果都简化成“那些以1%概率朝上的面”和“那些以2%概率朝上的面”和“那些以3%概率朝上的面”……以及“那些以99%概率朝上的面”。最终,我们把以这些概率出现的面的概率画成一张概率分布图。
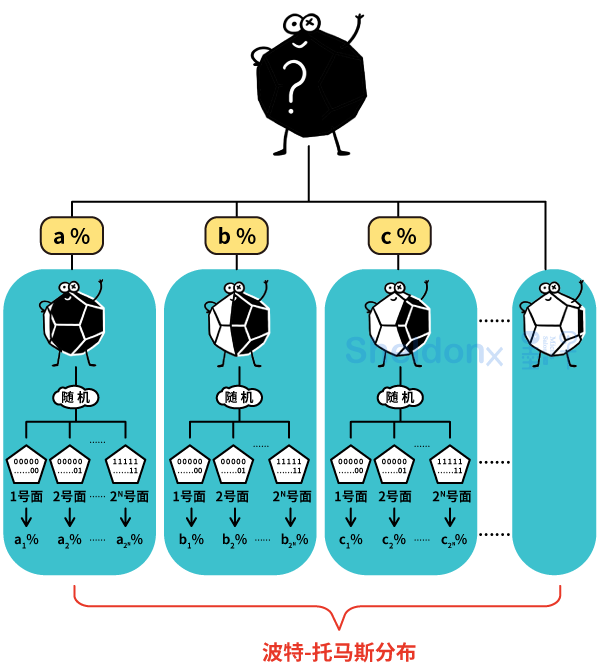
通过计算我们可以得出,当N很大时,这个概率分布图服从一种名为“波特-托马斯分布”的概率分布。
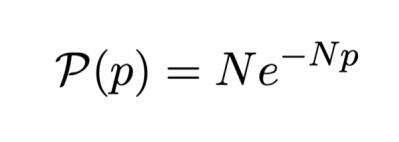
这就是物理学家对这个问题能给出的最好回答。
为什么这个回答比刚才的量子硬币还要绕呢?因为量子力学算出来就是这个结果。

由于计算过程涉及更复杂的数学知识,我就不具体讨论了。
反正你只需要知道,假如我扔出一枚具有2N个面的多面量子骰子,问会得到什么样的结果。正确的答案不是一组具体的概率值,而是一张“波特-托马斯分布”的概率分布图,就可以了。
那么问题来了,我们真的能用量子计算装置,实现扔2N个面的多面量子骰子的物理过程,从而证明量子计算的优越性吗?
答案是真的可以。只不过,在物理学的黑话体系中,这个过程不叫“扔2N个面的多面量子骰子”,而是叫“对N个量子比特的量子随机线路进行采样”。
四、祖冲之号2.0:56个量子比特的随机线路采样
2019年10月,在持续重金投入10余年后,谷歌成功开发了一个包含53个可用量子比特的可编程超导量子处理器,命名为“Sycamore(悬铃木)”。他们在上实施了一轮随机线路采样的实验,并正式宣布实验证明了量子优越性。
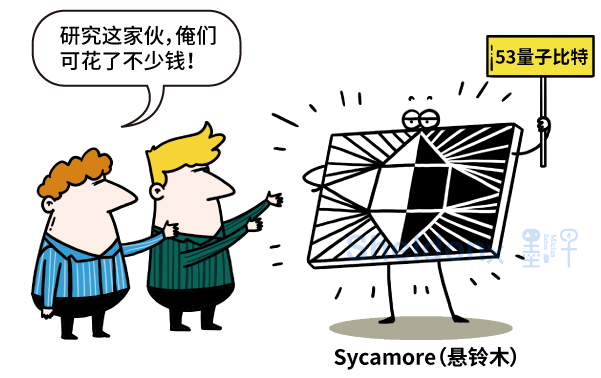
近日,中国科学技术大学潘建伟、朱晓波团队又研制了66量子比特可编程超导量子计算原型机“祖冲之号” 2.0。他们通过操控其中的56个量子比特,也开展了一轮随机线路采样实验,并成功地实现了量子计算优越性。

值得一提的是,“祖冲之号” 2.0的性能超越2019年谷歌“悬铃木”2-3个数量级。

他们的论文发表在了2021年10月25日的《物理评论快报》(PRL)上。

这个实验的原理很简单,就是制造出多面骰子,然后扔出去并记录结果,得到一个关于概率大小的概率分布。但实验步骤描述起来有点儿复杂。关心细节的同学可以看[注1][注2]。
那么,本轮实验实现量子计算优越性了吗?答案是肯定的。
本次实验一共扔了1900万次多面量子骰子,耗时1小时12分钟。
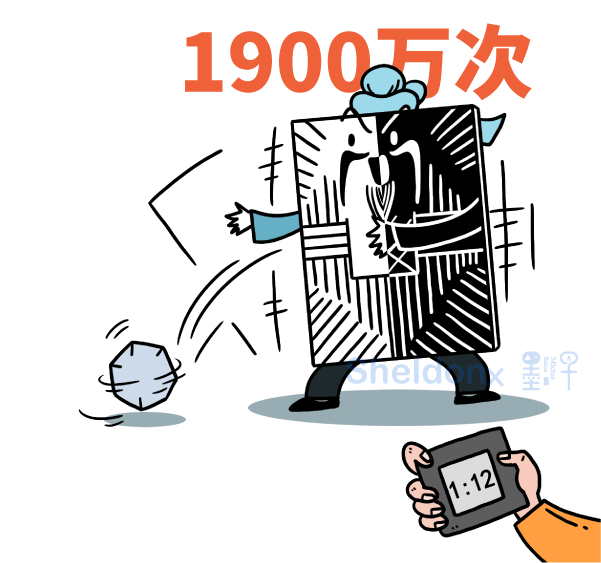
完成相同的任务,世界上速度最快的“Summit”超级计算机需要花费7年半的时间!

你可能会问,超级计算机的计算过程真的那么慢吗?答案是真的那么慢。我们看一看其中的数据量你就明白了。
我们平时说的1GB内存,大约可能容纳230个经典比特的数据。要想容纳256个经典比特的数据,我们就需要6千多万GB的内存。如果要容纳56个量子比特(需要256个复参数来描述)的数据,需要的内存容量就会更大,更不用说还要对它们进行复杂的运算了。
物理学家指出,用经典计算机计算多面量子骰子的概率分布,其计算复杂度属于NP-oracle难度。
因此,“祖冲之号” 2.0是真真正正地展现了量子计算的优越性[注3]。
值得一提的是,早在2020年12月,潘建伟、陆朝阳等人组成的研究团队,就在另一个不同的量子计算问题(高斯玻色采样)上,通过构建76个光子的量子计算原型机“九章”,展现了量子计算的优越性(《漫画 | 中国科学家研制出首个有潜在应用的量子计算原型机》)。

就在祖冲之号团队研发“祖冲之号” 2.0的同时,九章团队也没有闲着。他们对原先的“九章”进行升级,成功研发出了探测光子数为113个,探测模式数为144个的量子计算原型机“九章”2.0,将量子计算在高斯玻色采样问题上的优越性,从经典计算机(太湖之光)的1014倍大幅提高到了1024倍,输出态空间的维数则达到了1043量级,这使得问题的复杂度大大提升,更加难以被经典算法所模拟。
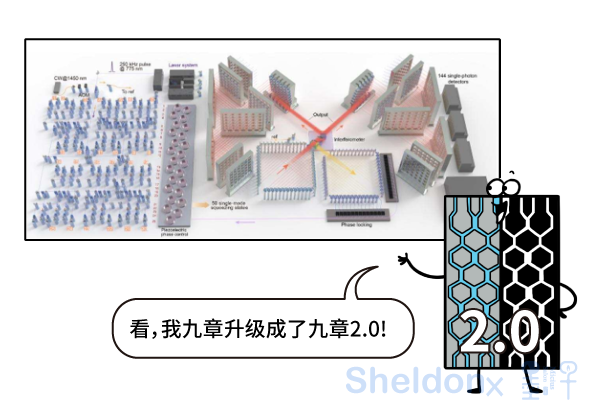
“九章”2.0与“祖冲之”2.0背靠背地发表在了2021年10月25日的《物理评论快报》(PRL)上。

于是,“祖冲之号”2.0连同“九章”2.0这两台升级版的量子计算原型机,使得我国成为第一个在多个不同物理体系中均实现“量子计算优越性”并取得领先优势的国家。
五、寻求量子纠错和更复杂的量子算法
说到这儿你可能会问?这就玩啦?研究组辛辛苦苦搭建了一个平台,仅仅是为了扔骰子吗?
并非如此。

这就好比一个军队在跟敌人作战之前,要进行射击、投弹、刺杀、爆破、土工等作战技能训练。虽然在训练中,士兵们并没有消灭真正的敌人,但这些训练有利于提高他们的作战技能,为将来在战场上消灭真正的敌人打下基础。
因此,你不要小看研究组让“祖冲之号”2.0、“九章”2.0掷“量子骰子”的工作。这项工作对物理学家来说,也是一种作战技能训练。

例如对于“祖冲之号”2.0的工作,当量子比特的数量和线路的层数增多时,量子计算的误差不但会随之增大,而且会变得越来越不可控。
具体来说,假如量子比特经过一层线路的运算后,理论准确率(即保真度)是99.6%;那么经过20层线路,理论准确率就应该等于(99.6%)20 = 92.3%。
但是,通常来讲,量子计算装置实际的准确率往往会远小于92.3%。为什么呢?这是因为量子比特和量子线路多了以后,就像三个和尚没水吃,相互之间会发生关联错误。这种关联错误不是某一个具体的量子比特或量子线路造成的,而是他们之间大规模协同时产生的。

然而幸运的是,在扔1900万次骰子的工作中,“祖冲之号”2.0没有额外的关联错误出现。它的准确率基本上等于量子线路准确率的乘积。这一点相当不容易。

而“九章”2.0的计算规模、复杂度比“九章”1.0大大提高,有两处值得关注的升级:
一是“九章”2.0开发了一款受激压缩光源,使得其关键指标从之前光源的63%,提高到了92%。用物理学黑话来说,它向高压缩量、高纯度和高收集效率的接近理想的压缩光源迈进了一大步。

二是“九章”2.0相比“九章”,增加了一定的可编程性。用物理学黑话来说,它实现了对光源相位的调控和锁定。

物理学家希望,他们可以通过一次又一次实验,逐渐掌握各种量子处理器的设计和使用技巧,为将来实现真正的量子纠错,和更复杂的量子算法,及各项技术在其他量子科技领域的应用打下坚实的基础。

注:
1. “祖冲之号” 2.0随机线路采样实验的大致步骤:
第一步,研究组让“祖冲之号” 2.0进入一种初始的量子状态。假如把这时的“祖冲之号” 2.0看作一个具有256个面的量子骰子,它的这种量子状态就相当于多面量子骰子的某一个面是朝上的。
第二步,研究组在“祖冲之号”2.0随机地搭建20层量子门电路。这些量子门电路的作用是,改变“祖冲之号” 2.0的量子状态,使它进入某种确定的量子叠加状态。这就相当于我们把第一步的量子骰子随机地制备到256个面同时朝上的一个量子叠加状态。
第三步,研究组通过测量“祖冲之号”2.0中的全部56个量子比特,得到一个确定的输出,比如,输出结果是01011.....01(共56位数字)。这就相当于把刚才制造的多面量子骰子扔了出去,得到了第57307...5号面朝上。
注意,完成这一步后,研究组就算完成了一次采样。完成采样以后,刚才制造的多面量子骰子就已经消失了。为了再进行一次采样,研究组必须再制造出一个多面量子骰子,把它扔出去,记录结果,同时它会再次消失。
所以,第四步,研究组对第一步、第二步和第三步重复1900万次,共完成1900万次采样,得到1900万个由0和1组成的56位字符串。
第五步,研究组将所有得到的字符串按照出现次数从少到多的顺序排列起来,得到一组关于概率大小的概率分布。然后与理论预言进行比较。
如果概率分布与理论预言相差较大,说明实验误差太大,实验失败。
如果概率分布与理论预言相差无几,说明实验误差在可控范围内,实验成功。
实验结果表明,本轮实验圆满成功。

2. 我们在理论上想要实现的采样步骤和实际上在“祖冲之号”2.0中实现的采样步骤略有不同。
理论上看,我们得随机制造N个许多完全不同的多面骰子,对每个多面骰子扔1次,才能得到我们想要的波特-托马斯分布。

实际上,我们不必把实验步骤设计得这么复杂,也能得到波特-托马斯分布。通过数学计算,我们可以证明,只要“祖冲之号”2.0的随机线路设计得足够好,我们只需要通过运行它,得到N个完全相同的多面骰子,对每个多面骰子扔1次,就能得到我们想要的波特-托马斯分布。

这里说的“随机线路设计得足够好”,就是指量子比特数要足够多,量子比特门电路的保真度要足够高,随机线路的层数要达到一定标准等等。这就是我们在最后一节提到的,实验物理学家所应对的挑战。
3. 相比之下,由于Google“悬铃木”的量子比特少一些,采样次数也有所不同,因此,使用“Summit”超级计算机完成经典模拟,只需要2天的时间。
参考文献:
1. Yulin Wu et al. Strong Quantum Computational Advantage Using a Superconducting Quantum Processor. Phys. Rev. Lett. 127, 180501.
2. Han-Sen Zhong et al. Phase-Programmable Gaussian Boson Sampling Using Stimulated Squeezed Light. Phys. Rev. Lett. 127, 180502.
3. 覃俭. 实验光学量子信息处理[D]. 合肥:中国科学技术大学,2021.
本文来自微信公众号:墨子沙龙(ID:MiciusSalon),作者:Sheldon

