北京时间11月1日消息,一些人认为,数学本身就存在于自然界中,等待被人们发现;而另一些人认为,数学完完全全就是人类大脑的创造。时至今日,这个问题依然没有确切的答案。对大多数人来说,解决数学问题和记住一长串数学公式是相当困难的。但是,你有没有想过,数学这门学科是否本身就存在于宇宙当中,等待被人发现?或者,数学只是有些人故意发明出来的东西?这些问题的答案就像微积分运算一样复杂。

毕达哥拉斯定理,即我们熟知的勾股定理
信不信由你,数学已经成为我们当今世界的中心。我们的智能手机、汽车、建筑甚至天气预报,都要依赖数学。从古至今,研究数学的哲学家们一直在争论一个重要的问题:数学究竟是被发现的,还是被发明的?
有些人认为数学就存在于我们的内心,数学所研究的对象是我们创造出来的。也有哲学家认为,数学独立于我们的思想而存在,与人类存在无关。但真相究竟是什么?我们只能在发明或发现之间进行选择吗?想要知道真相,首先让我们来了解一下数学的历史。

柏拉图是古希腊著名的哲学家和数学家,他认为数学实体是抽象的,独立存在于它们的世界中,在空间和时间之外
数学的历史有多古老?
数学的故事和人类一样古老,它已经从与牲畜数量有关的简单算术,发展成为对一个物体进行复杂研究的抽象概念。直到公元前600年,当人类文明稳定下来,各种职业开始出现时,数学才有了初步的发展。人们用数学来测量土地,或者计算个人税收等。后来,在公元前500年时,罗马数字出现了,它们至今仍然被用来表示数量。
科学家认为,像加减这样的基本数学函数可能在几千年前同时出现于印度、埃及和美索不达米亚等许多地方。高等数学可以追溯到2500年前的希腊,当时的数学家毕达哥拉斯给出了一个著名的方程——毕达哥拉斯定理,也就是我们常说的勾股定理。不过,历史学家相信这个定理——平面上的直角三角形的两条直角边的长度平方和等于斜边长的平方——早在毕达哥拉斯出生的一千年前就已经在世界各地广泛应用。
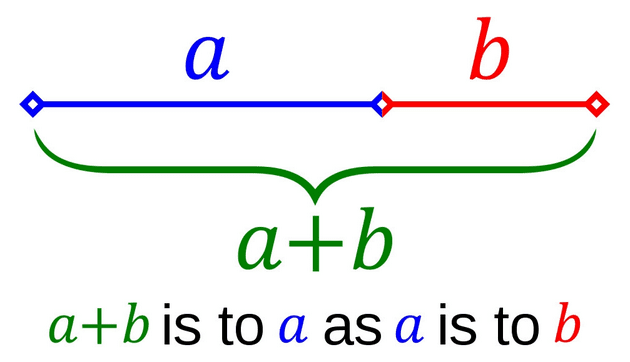
黄金比例公式
从那时起,越来越多的数学家开始努力扩展他们对数学的理解。然而,对于接下来这个重大的问题,还没有人能找到确切的答案。
数学本身就存在于宇宙中吗?
在历史的某些时刻,人们发现,有些东西在他们进行数学运算之前就已经存在;在另一些时候,人们会认为是自己发明了不同的方程和方法,将脑海里的东西记录下来。
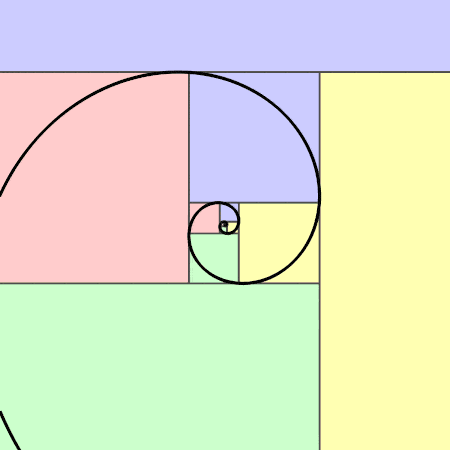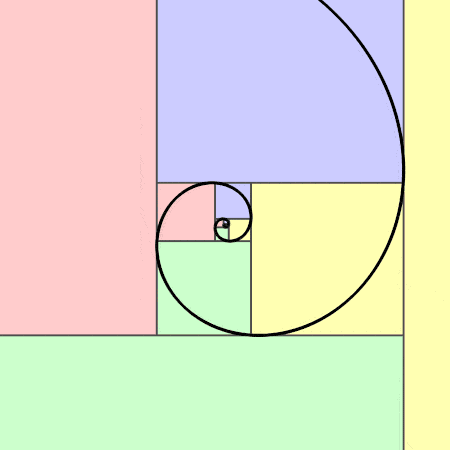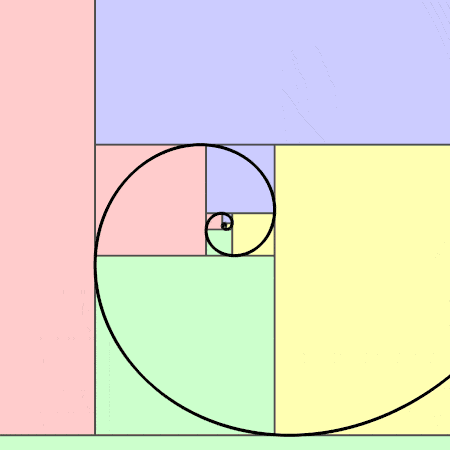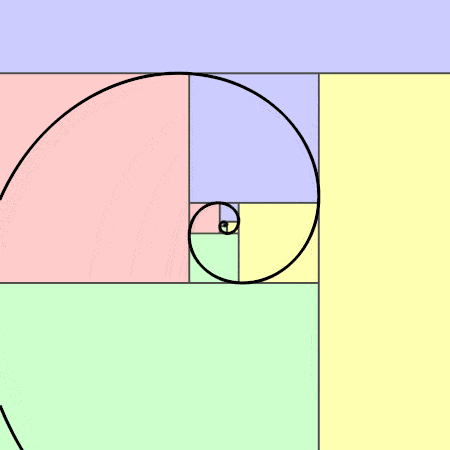
黄金比例
有人认为,与灯泡、电视等物品不同,数学并不是一项发明,而是一种发现。这种观点背后的思想是,数学存在于上帝或柏拉图式的思维世界中,而人类所做的就是发现它——这一立场被称为柏拉图主义。古希腊思想家和数学家柏拉图认为,数学实体是抽象的,独立存在于它们的世界中,在空间和时间之外。
有些数学思想非常基础,即使你没有发现,别人也会发现。数学是科学的语言,它的结构是自然、固有的。即使宇宙明天就消失,永恒的数学真理也仍然存在。我们有责任去发现它,理解它的功能,并在我们的知识基础上找到可以控制物理事件的解决方案。
许多数学家都支持这一观点。他们发现了许多永恒的真理,而这些真理——比如没有最大的质数,小数形式的圆周率可以无限延伸等——与发现它们的头脑无关。
数学本身可以在自然界中表现出来,并蕴藏着许多普遍问题的答案。在自然界中,我们经常可以找到一个与数学有关的例子——黄金比例。

赛菊芋属植物的花瓣呈斐波那契数列的模式
黄金比例与斐波那契数列
黄金比例描述了宇宙中最可预测的模式。它描述了从原子、飓风、人脸、人体到银河系的一切。黄金比例是两个部分a和b的比例等于(a+b)除以较大的部分a的值,约为1.618,用希腊字母φ 表示。它也被称为神圣比例。
黄金比例源于斐波那契数列,以意大利数学家列奥纳多·斐波那契的名字命名。数百年来,斐波那契数列一直令许多数学家、科学家和艺术家着迷。在这个数列中,每一个数字都是它前面两个数字的和,即0,1,1,2,3,5,8,13,21,34,55,……
我们可以在身边的各种事物中看到斐波那契数列,例如贝壳、动物、金字塔和其他意想不到的地方。花瓣也遵循斐波那契数列。如果仔细观察,你会发现一朵花的花瓣数可能是以下几种之一:3、5、8、13、21、34或55。例如,百合有3片花瓣,波斯菊有8片花瓣,玉米万寿菊有13片花瓣,菊苣和雏菊有21片花瓣,米迦勒雏菊有55片花瓣。这些现象支持了一个论点,即数学函数一直在自然界中存在着,我们所做的只是发现它们。
数学是我们创造的吗?
有些人反对数学被发现的观点,比如反柏拉图学派,他们认为数学是被发明的。换言之,数学是人类的一项发明,其设计方式可以恰当地描述物理世界。为了满足我们的需要,人类的头脑不断创造出各种数学概念。
如果宇宙明天就消失了,那么每一个虚构的想法,比如足球、国际象棋或我们发明的任何活动都会消失,数学也是如此。
人类可以通过观察自然界中出现的模式来了解宇宙的运作。通过从周围世界中抽象出形状、线条、群组等元素,我们创造出了数学概念,并将这些概念联系起来,以达到某种目的,或者只是为了好玩。
几何学和算术的发展来源于我们观察和区分形状的能力,如圆形、三角形等。我们也用几何来区分直线和曲线。
一开始,我们用的是自然数1,2,3……等来计算我们周围物体的数量。后来,我们发明了更多的概念,如负整数、有理数、无理数、复数等等。这些数学概念的扩展都是为了服务于我们的各种目的。
打个比方,如果水银计的温度降到0度以下。那么,为了说明一个小于零的数,我们就会引入负整数的概念,并写成-10℃或-25℃。正是由于这种基于周围所见而创造出新概念的过程,我们的确也可以说,数学诞生于我们的感知和心理设想。
有些人认为数学是一项发现,有些人则认为它是一项发明,这两种观点之间的争论可能会永远持续下去。考虑到这个问题已经存在了两千多年,在短时间内,我们应该不太可能找到完美的答案。不过,显而易见的一点是,数学并不在乎我们是否认为它是被发明的还是被发现的,或者两者在其存在中发挥了何种作用。不管我们对此的观点如何,数学都会客观地发挥它的作用,继续为人类造福。

