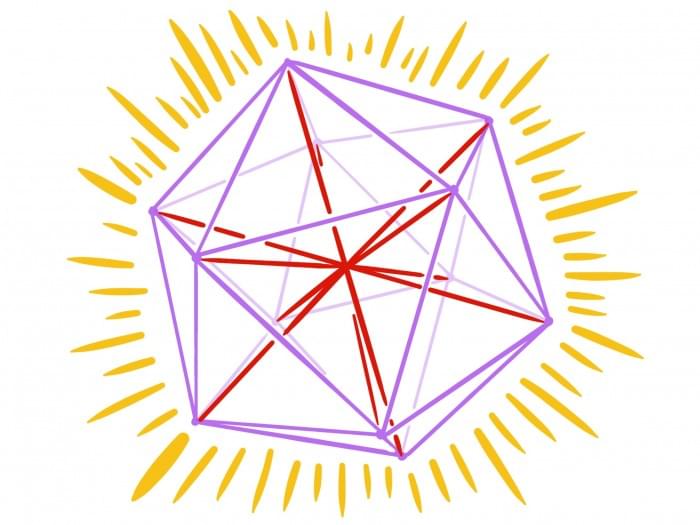
在高维空间中,有多少条线能以相同的角度成对分开?几何学上的突破使人们对谱图理论有了新的认识。等角线是空间中通过一个点的线,其对角都是相等的。想象一下二维的正六边形的三条对角线,三维的正二十面体的六个对顶点的连接线(见图)。然而,数学家们并不把假设的情况局限于三维空间。
数学助理教授赵宇飞说:"在高维度上,事情真的变得很有趣,而且可能性似乎是无限的。但根据赵和他的麻省理工学院的数学家团队,他们并不是无限的,他们试图解决这个关于高维空间中线的几何问题。这是一个研究人员已经困惑了至少70年的问题。他们的突破性研究决定了可以放置的线条的最大可能数量,以便这些线条以相同的给定角度成对分开。

Xiaodong Zhao与麻省理工学院的一组研究人员一起写了这篇论文,这组研究人员包括本科生Yuan Yao和Shengtong Zhang、博士生Jonathan Tidor和博士后Zilin Jiang。Yao最近开始成为麻省理工学院的数学博士生,而江现在是亚利桑那州立大学的一名教师)。)他们的论文将发表在2022年1月的《数学年鉴》上。
等角线的数学可以用图论进行编码。这篇论文为一个被称为谱图理论的数学领域提供了新的见解,它为研究网络提供了数学工具。谱图理论带来了计算机科学中的重要算法,如Google用于其搜索引擎的PageRank算法。
这种对等角线的新理解对编码和通信有潜在的影响。等角线是"球形编码"的例子,它是信息理论中的重要工具,允许不同方面在一个嘈杂的通信渠道上相互发送信息,例如美国国家航空航天局与其火星车之间发送的信息。
研究具有给定角度的最大数量的等角线的问题是在1973年P.W.H. Lemmens和J.J. Seidel的一篇论文中提出的。
普林斯顿大学数学教授诺加-阿隆(Noga Alon)说:"这是一个美丽的结果,为极端几何学中的一个精心研究的问题提供了一个令人惊讶的答案,这个问题从60年代开始就受到了相当多的关注。"
"当时有一些好的想法,但后来人们被难住了近三十年,"Zhao说。几年前,包括瑞士联邦理工学院(ETH)苏黎世分校数学教授Benny Sudakov在内的研究团队取得了一些重要进展,当时Sudakov在组合学研究研讨会上谈到了他在等角线方面的工作。
Jiang在卡内基梅隆大学的前博士生导师Bukh Boris的工作基础上受到启发,开始研究等角线的问题。Jiang和Zhao在2019年夏天组队,并邀请Tidor、Yao和Zhang加入。
这项研究得到了Alfred P. Sloan基金会和国家科学基金会的部分支持。Yao和Zhang通过数学系的本科生研究暑期项目(SPUR)参与了这项研究,而Tidor是他们的研究生导师。他们的成果为他们赢得了数学系的Hartley Rogers Jr. 最佳SPUR论文奖。"这是SPUR项目最成功的成果之一,不是每天都有一个长期的开放性问题得到解决的。"
解决方案中使用的关键数学工具之一被称为谱图理论。谱图理论告诉我们如何使用线性代数的工具来理解图和网络。图的"频谱"是通过将图变成矩阵并查看其特征值而获得的。
"这就像你把一束强烈的光照在一个图上,然后检查出来的颜色的光谱,"Zhao解释说。"我们发现,发射的光谱永远不可能过于集中在顶部附近。事实证明,关于图形光谱的这个基本事实从未被观察到。"
这项工作在光谱图理论中给出了一个新的定理--有界度的图必须具有亚线性的第二特征值多重性。该证明需要将图的频谱与图的小片的频谱联系起来的巧妙见解。

