
姜萍突围全球数学竞赛的事,发酵至此,彻底变了味儿。
“17岁中专生”,还是一个“女生”,两个tag相连,打开了看客们的质疑的大门——
女人怎么可能学好数学?
要么是她作弊了,要么这事背后有推手。
知乎上有张配图,把《让子弹飞》电影里的经典一幕,套用成对质17岁中专女生的现场。
效果传神得很。



——“我没有作弊,我就是喜欢数学。”
——“作弊了!一定作弊了!虽然我不懂数学,但从我个人生活经验来看,她一定作弊了!一个中专女生怎么可能学好数学?”
这种毫无根据烂在根上的论调,恐怕17岁的姜萍看了,也有苦难言。
一百张嘴也说不清楚。
当一个小概率事件突然突破大众原本的认知,总有人困在自我有限的认知里,并拒绝承认他人的优秀。

01
人类世界发展以来,女性真的比男性更不擅长数学吗?
这一“刻板印象”,或许从根源上,就是偏见。
因为在微分不等式、环和理想子群等方面的伟大成就,埃米·诺特影响了世界数学界,是20世纪的著名数学家。
埃米·诺特出生于19世纪80年代的德国,父亲是埃朗根大学的数学教授。
1908至1915年间,诺特在埃朗根数学研究所工作,在此期间她没有任何头衔和收入。
因为性别、政治或宗教原因,没有任何收入和认可,是她人生的常态。
但她不输男性的数学才干,仍然被一些人所看见,并在众多反对声中成为哥廷根大学的讲师。
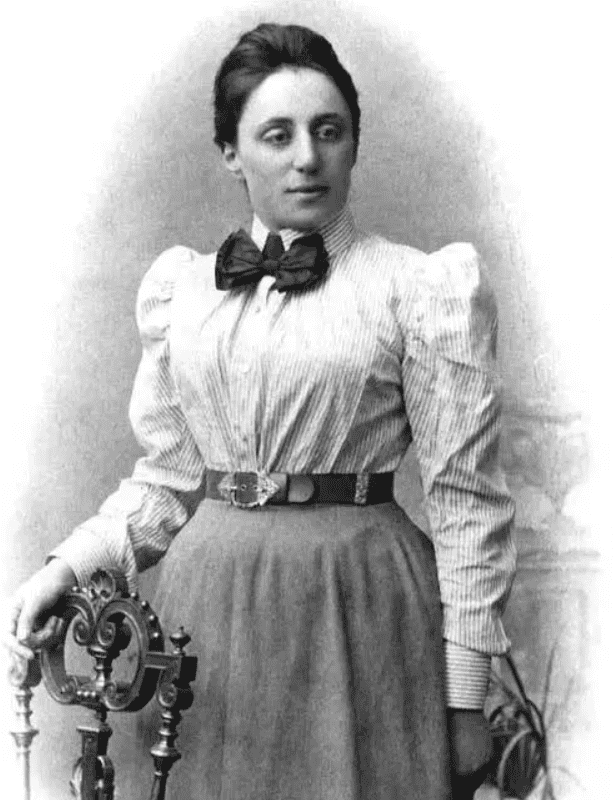
埃米·诺特
女性真的更不擅长数学吗?
再讲一个小故事。
18世纪70年代出生于法国巴黎的索菲·热尔曼(Sophie Germain),大量时间都泡在父亲的图书馆中,因此对数学迸发出兴趣。
父母却不赞同她对数学的兴趣,并想方设法阻挠她。
但就算父母停掉热尔曼的暖气和照明,热尔曼还是想尽办法反抗并坚持学习。

热尔曼对数学的兴趣,不仅得不到家里的支持,也不被当时的学校所接纳。
由于当时的巴黎综合理工学院不允许女性听课,热尔曼只能弄到上课讲义自学。
后来得以散发自身光热,是因为她以假名提交了一篇论文,被导师拉格朗日看重。
出于赞赏,拉格朗日成为热尔曼的导师,为热尔曼打开了继续研究数学的大门。

索菲·热尔曼
之所以历史上没有更多女性数学家,受社会环境影响因素很大。
很长一段时间里,女性不被允许学习数学,不被允许上学。
反过来因此质疑女性的数学能力低男性一等?
这显然没有道理。
02
研究表明,男性和女性在数学方面没有认知生物学上的差异,男性“数学更好”的说法并不正确。
这个“误解”,不止流行于美国。
哪怕历史早已更新迭代,在世界多数地方,仍然存在这样的“误解”。
早期经历、生物因素、教育政策和文化背景,无一不在影响着追求科学和数学高等教育的男女人数。

相关论文
这些影响以复杂的方式叠加和相互作用。
当下普遍语境和研究都在表明,对于科学和数学中性别差异的复杂问题,没有单一或简单的答案。
姜萍作为女性在数学领域不被看好,一定程度上,也是受到此类历史因素影响的结果。
然而看客们忽略的客观事实是,
由于日常只用学“语数外”和服装专业课,姜萍在进入涟水中等专业学校后,反而有了充足的课余时间跟数学相处。
在这所中专里,她遥遥领先的数学成绩,很快引起了数学老师王闰秋的注意。
本着对数学同样的热爱,王闰秋开始指导姜萍学习高等数学。
在老师眼里,姜萍不属于天才型,而是属于“勤奋型选手”。
姜萍几乎所有的课余和晚自习时间都沉浸在数学的世界里,有时做题会做到夜里一两点钟。
观念的形成,从来是潜移默化的。
女性学不好数学,才是最大的PUA。
03
再往前一步,就算脱离了性别标签,看客们还可以从考试形式入手声讨。
“48小时开卷考试,这样的考试有啥真实性?
不信看决赛成绩。

当然允许合理质疑。
但这场竞赛的“开卷”,和网友们以为的“开卷”有别。

随意否定姜萍努力的人,怕是根本不了解这场竞赛有多难。
其实从考试结果,就能窥见一二。
今年的阿里巴巴全球数学竞赛预选赛题目共有7道题,最后入围分是45分。
在历届的阿里数赛中,都算难度不低,没有满分选手。
姜萍得了93分,同等条件下,的确超越了一众名校出身的竞赛选手。
这场竞赛之所以采取开卷形式,是由于考题不仅考察参赛者的数学知识,还考察参赛者的综合能力。
既符合数学逻辑的特性,也从更多层面保证了比赛的公平性。

考题第1题,图源:数学中国
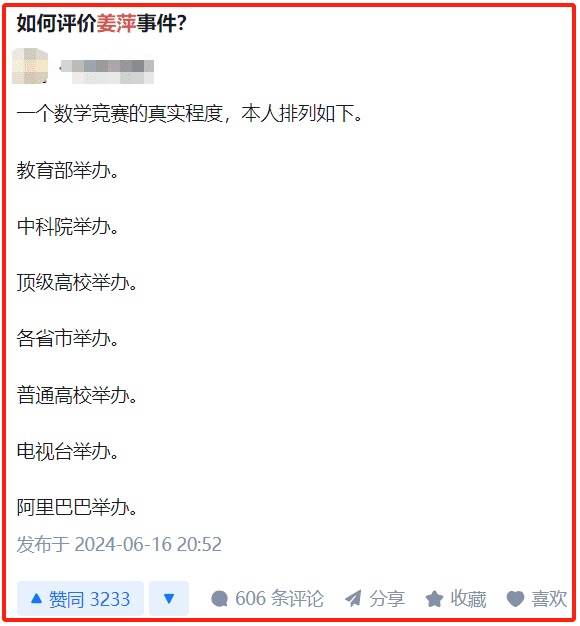
还有网友,做了一个个人主观意识上的“数学竞赛真实程度的排列”,结果如下:
教育部举办﹥中科院举办﹥顶级高校举办﹥各省市举办﹥普通高校举办﹥电视台举办﹥阿里巴巴举办
收获了3233个赞。
这场比赛的含金量到底如何,组委会名单可以作为一项参考。
随便哪个,都是妥妥的大佬。

阿里巴巴全球数学竞赛组委会名单(部分截图)
更何况,这种通过列表对比,怀疑竞赛真实性的角度,本身就充满了偏颇。
04
姜萍的爆红,让名单里的一众名校生成了陪衬。
当然,没必要神话姜萍。放眼中国,和姜萍一样优秀或者比姜萍优秀的大有人在。
无可置疑的是,从中专自学逆袭突围进入大众视线的姜萍,自身有着非常亮眼的成绩和韧性。
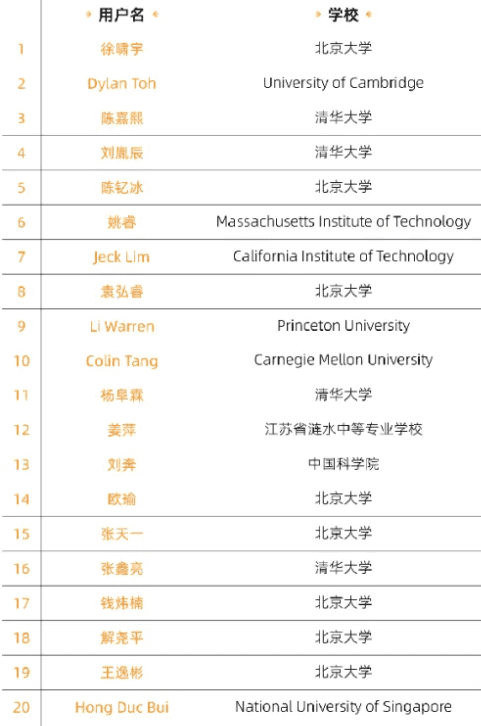
把姜萍换成任何一个名校生,都不会有这样的新闻效果。
一个是大众观感上的“理所应当”,一个是大众最爱的“逆袭”故事。
正是因为发生在中专生身上了,也显得足够特别和耐人寻味。

最后,奉劝一些网络看客,自己做不到的事情,不代表别人不行。
天外有天,人外有人。
承认别人优秀,是自我走向优秀的开始。
放过姜萍,让舆论熄声。
让她专心备考,继续专注于自己脚下的路吧。
这才是对人才最大的成全。

