本文来自微信公众号:中科院物理所 (ID:cas-iop),作者:黄水机,原文标题:《ChatGPT大升级?它去考研能考上物理所吗?》,题图来自:《天才枪手》
3月15日本应是小编勤勤恳恳搬砖的平凡一天,但小编刚睡醒就发现朋友圈被ChatGPT刷屏了:新版GPT-4震撼发布!
这些字眼引起了我的兴趣,于是小编迅速入(ke)手(jin)了GPT-4,经过简单体验后,小编发现ChatGPT的思维深度确实比之前有了跨越式的提升,高中甚至大一大二的知识根本难不住它,于是小编准备对它进行进一步测试......
如果你还不太了解什么是ChatGPT,可以先看一下我们先前的推送:《假如ChatGPT去考物理,可能会挂科》。
在上一篇推送中我们已经简单测试了ChatGPT的物理水平,但结果并不尽如人意。它仍停留在对物理学一知半解的阶段,很多知识点仅限于知道,稍微深入就开始顾左右而言他,逻辑思维能力有限,但那是之前的GPT-3.5版本。
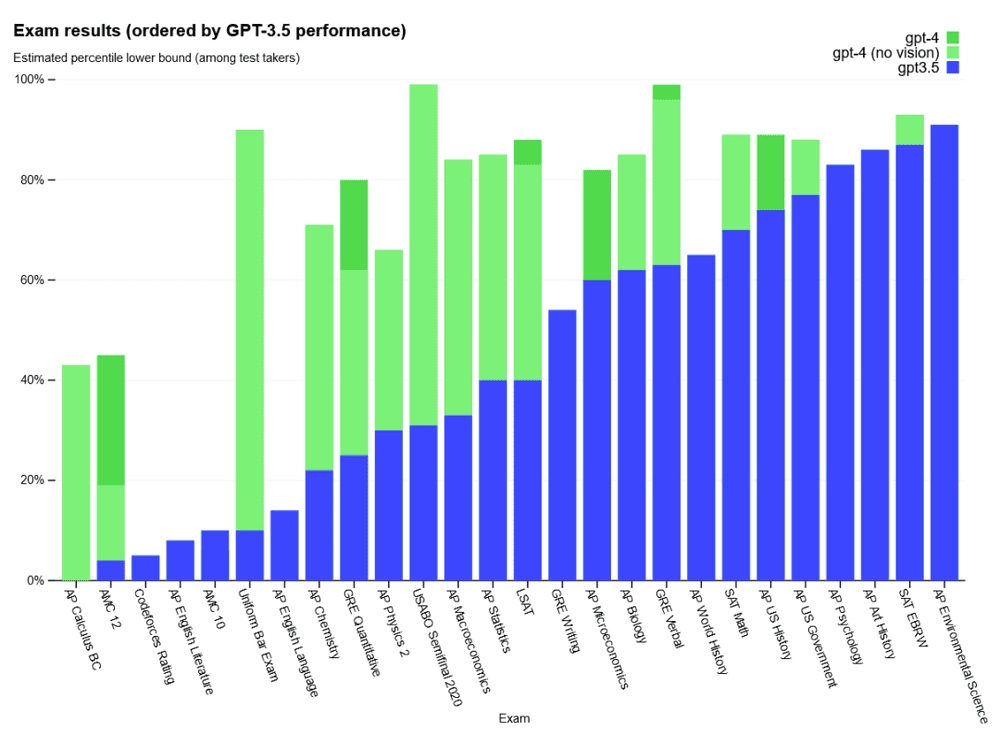
根据官方的宣传,新推出的GPT-4在各项考试中的成绩远超GPT-3.5,在很多专业和学术上的表现达到了人类水平,甚至在GRE(美国研究生入学考试)的两科中已经达到了顶尖大学生水准。
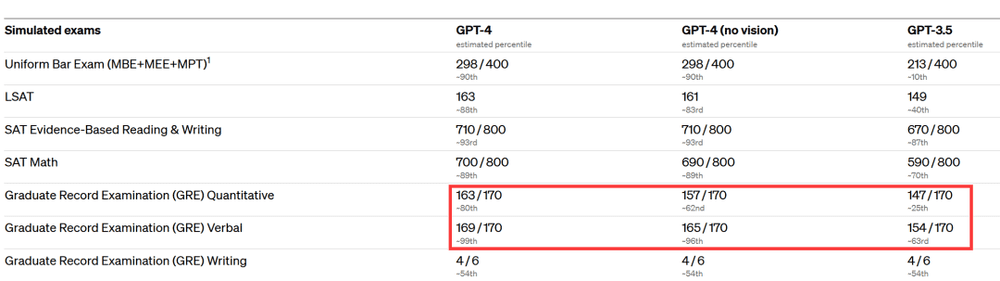
于是小编开始好奇:它能征服GRE,能征服我们物理所的考研题吗?

物理所的考研专业课是国科大自主命题。根据往年的情况,专业课单科分数130左右(满分150分)才能有一定把握考上。

由于不同专业的考试要求不同,这里我们就以四大力学中最难的量子力学作为基准来考察一下新版ChatGPT的物理水平。至于为什么要选量子力学,因为普物对它已经构不成威胁,测不出它的能力上限,是时候让ChatGPT见识一下真正的力量了。
温馨提示:看不懂也不影响你直接拉到文末看结论。
一、量子力学第一题

第一问:

第一题的三问都是量子力学基础内容,属于送分题,但从这个答案就可以看出ChatGPT是有量子力学功底的:能充分理解我给出的题目,思路清晰正确,加十分。
第二问:

本题ChatGPT用的方法很奇怪。因为题目没有给出束缚态的具体形式,也就没有值得讨论的对称性,只能勉强给一点分。
实际上定态下力学量的期望值不随时间改变,具体到位移就是d<x>/dt=0,用海森堡运动方程可以导出<p>=m*d<x>/dt=0,因此的动量期望为0。
第三问:


本题其实只需要将含时薛定谔方程的解代入定态方程,求出其对时间的导数为0就可以,ChatGPT却大费周章地去求含时薛定谔方程的解,实际上这个结论完全可以直接使用。
而且ChatGPT还差临门一脚:证明对时间的导数为0,不过影响不大。
第一题得分:22分。
二、量子力学第二题
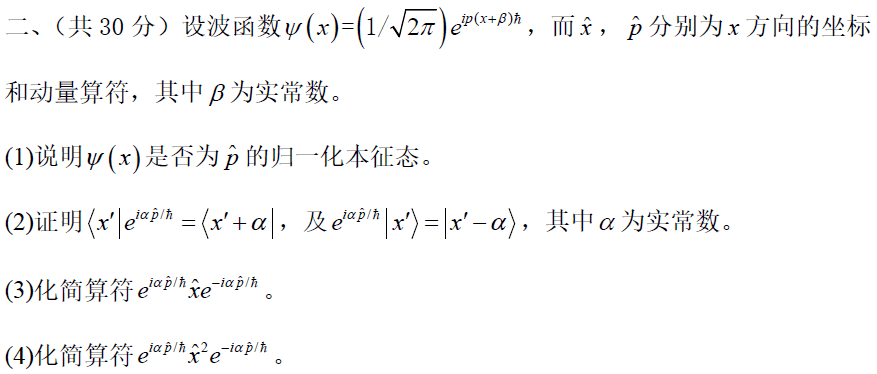
第一问:

首先是本征态没问题,但归一化错了。积分的结果应该用delta 函数,否则对1进行全空间积分就是正无穷。但如果我们跟着ChatGPT的错误思路继续做下去,就会看到最后一步化简时AI给出了这样的结果:
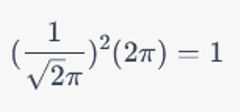
这个式子的值应当是1/π。居然会出现这种低级错误,ChatGPT你还是训练得不够啊!
第二问:



第二问用泰勒公式就扯远了。本题两个结论之间是厄米共轭的,只需证明其中之一。解题思路是在两项中插入一个完备集,运算后积分即得结论。
第三问:


第三问的过程乍一看还是很合理的,公式本身也没错,但AI却套错了公式导致结果错误。正确的公式如下:
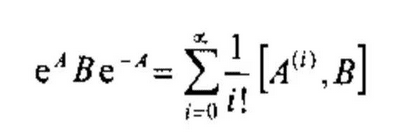
第四问:

第四问ChatGPT的思路没错,只需要将第三问结果平方就能得到结果,但第四问要用到第三问的结论,所以也跟着错了,大概可以酌情给点思路分。
第二题得分:10分。
三、量子力学第三题

第一问:来看看ChatGPT对角动量的理解。


看起来ChatGPT并不懂角动量,说了一堆废话以后算出来一个0,正确的解法应该把球坐标代入波函数,然后整理成球谐函数的形式算出角量子数l=1。
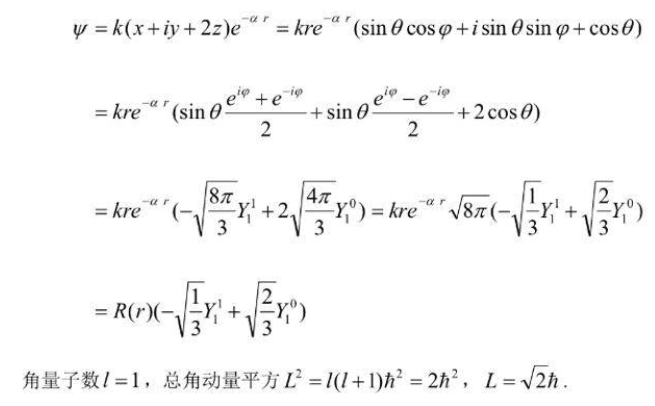
如果总角动量为0,第二问的结果直接就是0,就不需要算了。
第二问:

果然,ChatGPT废话了一大圈以后还是得出了0,第一问总角动量算错,第二问算分量肯定会算错。
至于第三问,ChatGPT废话说到一半就报错了,所以我就不上截图了。
第三题得分:2分。
四、量子力学第四题

第一问:

第一问的解题思路是对的,然而ChatGPT一上来就把哈密顿量给写错了,少了泡利矩阵里的1/2,因此最后的本征值里多了个2,且结果没有归一化,但除此以外都是对的。
第二问:


第二问是纯粹的本征值计算问题,ChatGPT的思路非常标准,前期计算也是正确的,但最后算行列式时直接把两个2c_0给扔掉了,导致两个能级结果错误。虽然没能全对,能做到这一步已经很厉害了。
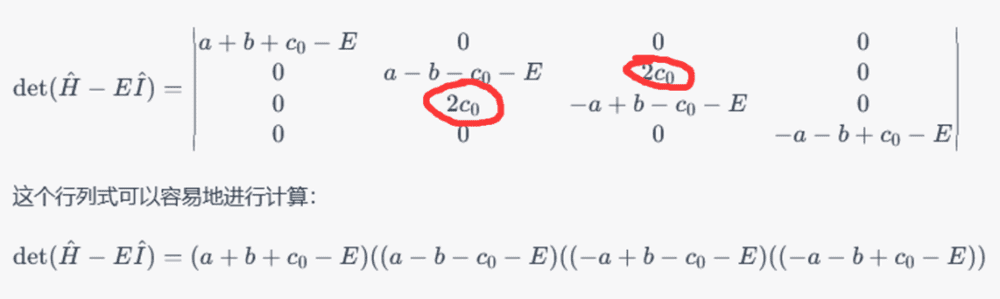
第四题得分:25分
五、量子力学第五题


第一问是送分题,只要把定态的动量和位移的不确定度代入不确定性关系,由a^2+b^2≥2ab就可以导出最小值,ChatGPT的思路虽然复杂了点,但也没问题,然而它又又又又算错了:
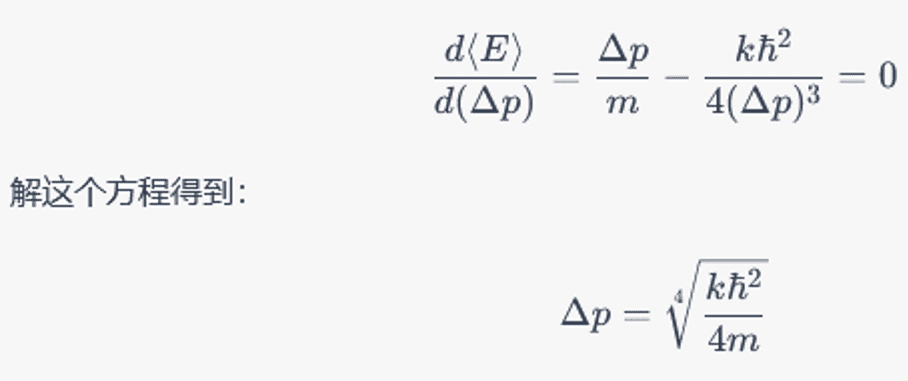
但我们稍加计算就能看出这里的化简结果应当是:
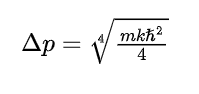



第二问变分法,ChatGPT一上来就把归一化常数算错了:
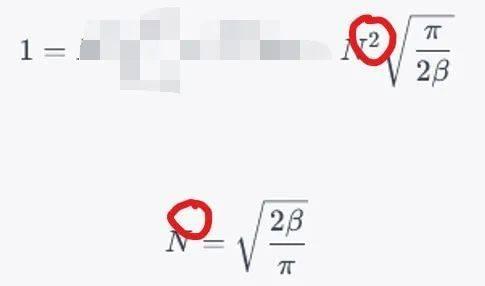
但人类也会犯这种低级错误。很明显,这里AI把平方漏掉了,导致后续计算全部错误。不过AI给出的过程很标准,条理清晰,值得学习。
第三问:

本题直接套升降算符的性质:a_- |0>=0,|1>=a_+ |0>,由第一个式子确定基态波函数,再用第二个式子算出第一激发态。AI用的也是这个思路,但在下面这一步求导的时候算错了。
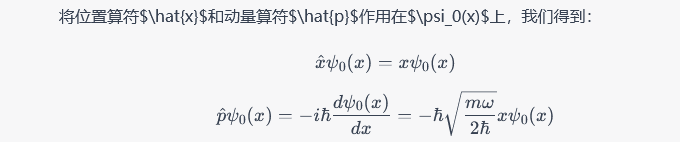
第四问:

题目已经给出了微扰的矩阵形式,直接算特征值就可以解决问题,但ChatGPT又把简单的行列式算错了,算出了1*1=2的惊天妙手:
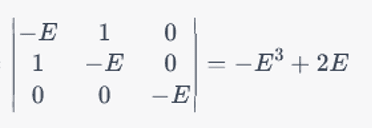
正确的久期方程应该是-λ^3+λ=0,而不是其给出的-λ^3+2λ=0。由久期方程解出0和±1三个特征值,因此在微扰下三重简并消除,能级分裂成与特征值一一对应的三个。
第五题总分:18分。
ChatGPT总得分:77分/150分,距离130分的目标还有亿点差距,建议第二年再战哦。
此外,我还让ChatGPT做了2021年的国科大量子力学考研题,它也拿到了约80分,而且如果能帮它稍微修正一下计算过程中的错误,就能达到约100分水平。毫不夸张地说,ChatGPT的量子力学已经达到了物理系本科毕业生水平。
六、文献总结
为了进一步测试GPT-4的学术能力,我又找了一篇文献来测试GPT-4的文献阅读能力,下面是一段由其生成的文献内容总结:

ChatGPT翻译总结的错误较多,比如温度的单位mK被翻译成了毫克,也无法理解一些学术名词,比如1K池(4He-1K-stage)被翻译成了1K级,不认识卡皮查热阻等,参考价值有限。看来学术名词翻译即使对AI来说也不是一件容易的事。

但如果让ChatGPT以英文输出,则其总结文献内容的能力十分强大,语言流畅逻辑清晰,不过仍会遗漏一些重要信息,所以还不能依赖AI来看文献。
目前将论文输入ChatGPT比较麻烦,很多时候不如直接看摘要,尚不能为我们阅读文献提供实质性的帮助。如果后续能根据图片或者pdf直接给出主要内容,将是其能力的又一次飞跃。
七、新旧版本对比
最后我又对比了一下GPT-3.5和GPT-4的量子力学能力。面对一维谐振子问题,GPT-4能完美解决,但GPT-3.5就不行。

不过,面对更复杂的场论中氢原子狄拉克方程与精细结构问题,即使是GPT-4也无能为力,只能在说了一堆废话后报错,看来场论的难度已经超过了它的能力上限。综合来看,GPT-3.5对量子力学仅有大概了解,但GPT-4对量子力学有着深入的了解,水平远超GPT-3.5。




GPT-3.5和GPT-4的对比,第一张截图是GPT-3.5,后三张是GPT-4。
八、总结
经过测试,GPT-4对量子力学的理解相当深入。它解题的思路清晰准确,但计算能力较差。由于语言模型底层逻辑的限制,它在解题过程中总是犯低级计算错误,因此拿不到高分,也就考不上物理所。但我认为它的总分过国家线不成问题。
虽然ChatGPT很难考上物理所,但它的量子力学水平已经接近物理专业的本科毕业生(计算能力除外),令人不得不承认它的强大。不仅如此,从小学中学到本科的题目都可以让ChatGPT来解,其不但能提供详细的思路和过程,还能针对你提出的问题加以讲解,善加运用完全可以成为学生的好帮手。
注1:ChatGPT网页端目前未开放图片输入,本文并非以图片,而是以输入符号文字的形式来向ChatGPT提问的。展示的题目图片是为了方便读者阅读。
注2:小编没有考研经验,给分比较随意,本文不构成任何考研建议。
本文来自微信公众号:中科院物理所 (ID:cas-iop),作者:黄水机

