
从1950年代开始,苏联的铁路系统就开始研究最大流问题。“它可能比计算机科学的理论还要古老。”加州山景城谷歌研究中心的伊迪丝·科恩 ( Edith Cohen ) 说道。这个问题有很多应用:互联网数据流、航空公司调度,甚至将求职者与空缺职位匹配。

从左上角顺时针方向:Yang Liu、Li Chen、Rasmus Kyng、Maximilian Probst Gutenberg、Richard Peng 和 Sushant Sachdeva
经过长久的努力,这个问题于近期出现了突破性进展——六位计算机科学家的新算法可在“几乎线性”的时间内解决这个问题,这意味着该算法的运行时间大致与首次写下该网络细节所花费的时间相当。对于所有可能的网络,解决这些问题的其他算法都无法达到如此快的速度。同时,这个新算法也处理了如何在最大流的同时最小化成本。

“简直太棒了。”加州大学伯克利分校的Satish Rao表示,这个结果让他跳了起来。
“现在我们知道我们可以非常快速地做到这一点,人们将会由此发现各种各样他们以前没有考虑过的应用程序。”耶鲁大学Daniel Spielman表示。
目前,这主要是理论上的进步,因为速度提升只适用于远大于我们在现实世界中会遇到的网络。对于目前现实中会遇到的网络,最大流量问题已经可以被相当快地解决(至少在不涉及最小化成本时候是的)。即使如此,该算法的六位创造者之一、加拿大滑铁卢大学Richard Peng预测,新算法的某些部分可能也会在一年内得到实际应用。研究人员表示,在未来几年,计算机科学家可能会找到使其更实用甚至更快的方法。
“即使确实出现了改进,这篇新论文也是‘灌篮高手’。基本上是最好的。”麻省理工学院Aleksander Mądry说。

解决最大流问题的第一个算法一般追溯到1956年。当时Lester Ford和Delbert Fulkerson使用“贪婪”方法解决此问题,即在每一步都使用最容易获得的对象。
想象一个运输公司希望从洛杉矶向纽约一次性派出尽可能多的卡车。Ford和 Fulkerson的算法首先会选择从洛杉矶到纽约的一条路径,并沿该路径安排尽可能多的卡车。但这通常不会利用该特定路径上所有道路的全部容量,因为如果这个路径的一部分是一条五车道高速公路,但它通向一座两车道的桥梁,那么在任何时候都只能一次安排两辆卡车。
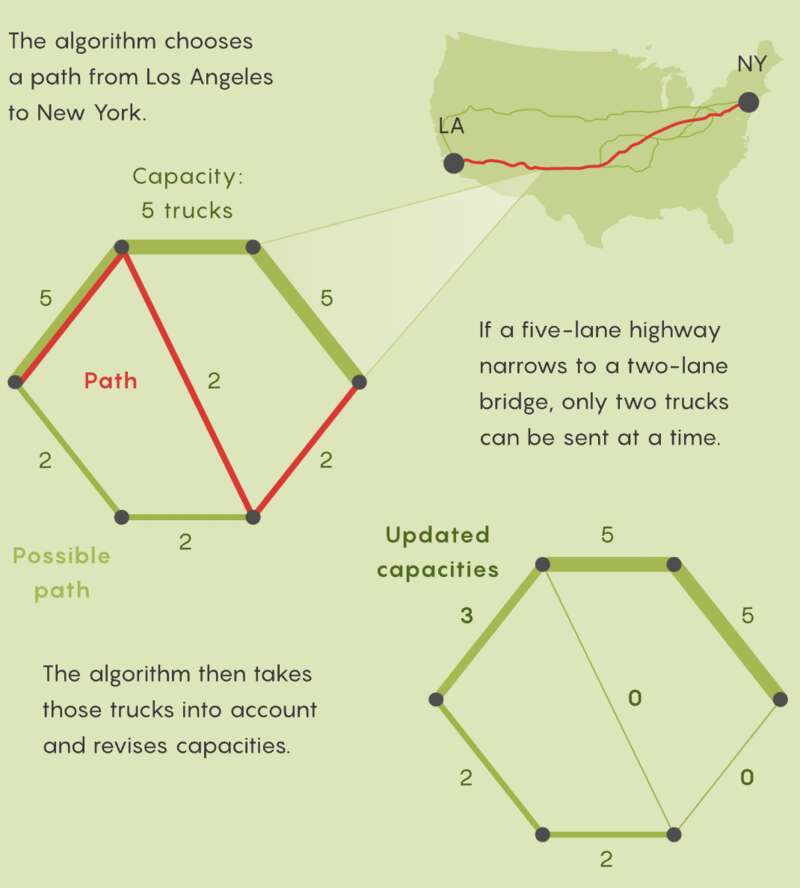
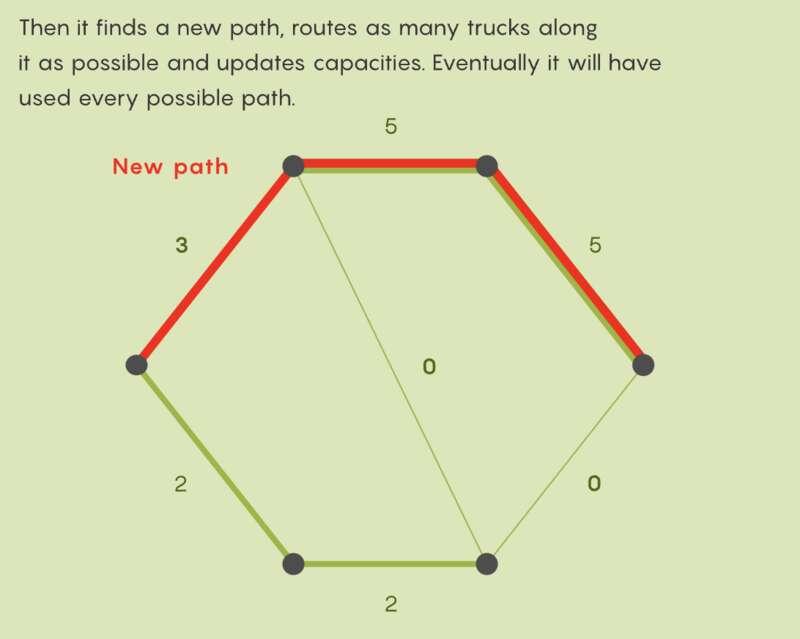
然后,该算法会找到一条从洛杉矶到纽约的新路径,沿该路径发送尽可能多的卡车,并再次更新容量。经过有限数量的这些步骤,从洛杉矶到纽约的路径将无法容纳更多卡车,然后只需将所有流程组合起来,就得到一次最大可能安排的卡车数量。
在该算法发表后的几十年里,研究人员试图通过让算法做出更明智的选择来加快运行时间。此后经过多次突破,这个运行时间再难低于m^1.33(Ford-Fulkerson算法是m^2),其中m是网络中的链接数。
人们开始怀疑这个指数是不是一个基本极限。理论上,最大流算法的最快可能运行时间将是m(即m^1),因为仅仅写下一个网络就需要m步的倍数,这被称为线性时间。但对许多研究人员来说,如此快速的算法似乎是不可想象的。
“没有充分的理由相信我们可以做到这一点。”Spielman说。Mądry曾减少解决最大流问题所需的步骤数,但这种减少是有代价的:在每一步中,都必须重写整个网络,并从头开始解决问题。
这篇新论文的六位研究人员想到一个新的思路,同时实现最小成本算法解决最大流量问题。想象一下,你创建了一条将卡车从芝加哥沿收费公路运送到纽约的流程,但随后发现有一条更便宜的高速公路可用。增加从纽约开始的循环,沿着昂贵的道路运行到芝加哥,然后沿着更便宜的路线返回,这就有效地用更便宜的路径取代昂贵的路径,从而降低了总成本。
加拿大维多利亚大学Valerie King说,这种方法使用了更多步骤,“听起来像是在倒退”。作为补偿,算法在每一步都必须非常快地找到一个好的循环——这比检查整个网络更快。
这其中使用到了一种“低拉伸生成树”(low-stretch spanning tree)新方法——一种捕获网络中许多最显著特征的内部主干。给定这样一棵树,总可以通过从树外部添加一个连接来构建至少一个良好的循环。因此,拥有低拉伸生成树会大大减少需要考虑的周期数。
即使这样,为了让算法快速运行,团队也无法在每一步都构建一个全新的生成树。相反,他们必须确保每个新循环仅在生成树中产生轻微的涟漪效应,以便他们可以重用之前的大部分计算。论文作者之一、斯坦福大学研究生Yang P. Liu说,达到这种控制水平是“核心难点” 。
最终,研究人员创建了一种在“几乎线性”时间内运行的算法,这意味着在越来越大的网络中,它的运行时间接近m。
责任编辑:李跃群

