本文来自微信公众号:量子位(ID:QbitAI),作者:博雯、梦晨,原文标题:《Nature最新封面:两大数学难题被AI突破!DeepMind YYDS》,头图来自:视觉中国
现在,AI不仅能参与数学研究,甚至还快人一步,开始帮助人类提出数学猜想了。
这只由DeepMind与顶级数学家合作研发的AI,登上了最新一期Nature封面。

有多顶级呢?这些数学家全部都来自牛津大学、悉尼大学,其中还不乏英国皇家学会史上最年轻的院士。
就是这位,曾在两年内斩获谢瓦莱奖、克雷研究奖等4项数学大奖的Geordie Williamson:

对于这项研究,DeepMind官方自称其“首次证明了人工智能可以走在纯数学研究的前沿”。
为什么这次的研究被Nature评价为“AI与人类合作”甚至是“AI指引人类直觉”,与“人类使用AI工具”有何不同?
首先我们要知道,证伪一个猜想相对简单,只需要找出一个反例即可。
但从零开始提出一个全新猜想这种工作,AI还是首次参与进来。
猜想本身是推动数学发展的一大动力,世界近代三大数学难题都是猜想:费马猜想、四色猜想和哥德巴赫猜想。
此前提出猜想主要靠少数科学家的洞察力和个人经验积累,比如历史上两位天才,物理学家爱因斯坦和数学家拉马努金。
但随着科学不断发展,需要研究的问题复杂程度逐渐超出人类能力极限。
有的问题涉及的数据规模,是一个人一辈子也研究不完的。
有的研究对象复杂程度之高,甚至可以有几千个维度,超出了一般人类大脑从直觉上可以理解的能力。
除此之外,这次研究也帮忙搞了搞数学领域内存在了40年的陈年老题,得到了不小进展。
参与这次研究的数学家之一,牛津大学的Marc Lackenby说:
我很震惊机器学习在直觉指引上的作用这么大,也没想到我过去先入为主的一些观念被AI给颠覆了。
没有参与这次研究的另一位数学家,以色列特拉维夫大学的Adam Zsolt Wagner也很羡慕:
如果没有这个工具,我们数学工作者可能会花上数周至数月的时间,最终发现证明的公式或定理是错误的 。
那么,AI这次到底帮助数学家们解决了哪些问题?下面来一探究竟。
AI发现代数和几何间的联系
第一个问题关于纽结理论(Knot Theory),是拓扑学的一个分支。
用数学语言来讲,纽结是一个圆在三维实欧氏空间中的嵌入。
呃……还是看图吧。
假设你有一根绳子,打上一个结。

再把两端粘起来,这就是一个纽结 (Knot)了。

结可以多打几个,比如这样:

或者,这样?

数学家倒是不关心纽结到底是用鞋带还是面包做的,他们最关心一件事:
一个复杂的纽结能不能被还原成简单的纽结,如果能就说明这两种纽结在拓扑上是等价的。

以此为依据给纽结分类,才能理解它们的性质,进一步与实际应用问题建立联系。
纽结理论在现实世界中,可以用来确定一个化学分子是否有手性,还有希望靠拓扑量子计算模型构建出量子计算机。
数学家们从几何特征和代数特征两个角度去研究纽结,分别定义了纽结的几个属性。

但问题难就难在纽结的种类太多,自19世纪以来人类已经收集了无数种,如果用上计算机自动生成,现在每天都能生成几十亿种。
普通人难以从海量数据中发现隐藏的模式,AI这次却做到了。
AI的贡献是发现了纽结的几何特征和代数特征之间存在直接的关联。
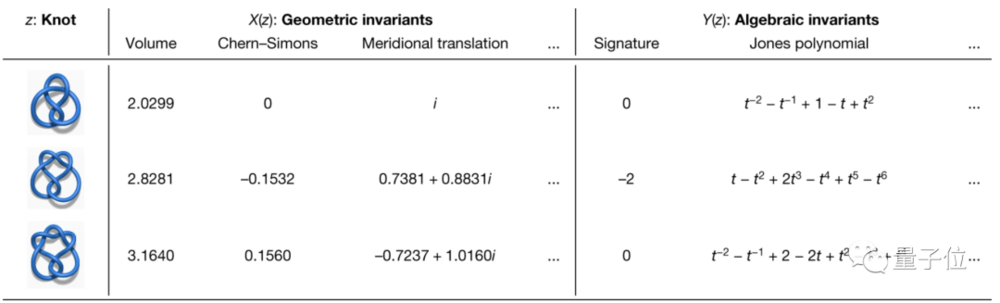
数学家由此发现提出猜想,再给出严格证明,为纽结问题研究开辟了新的方向。
40年难题终于有望得证
除了解决了扭结问题之外,另一个则与表示论 (Representation theory)相关。
表示论是数学中抽象代数的一支,表示的所有构件都不可约。
而这种不可约表示(Irreducible representations)的结构主要受Kazhdan-Lusztig(KL)多项式的影响。
组合不变性猜想(Combinatorial Invariance Conjecture)就是与KL多项式相关的一个重要猜想。
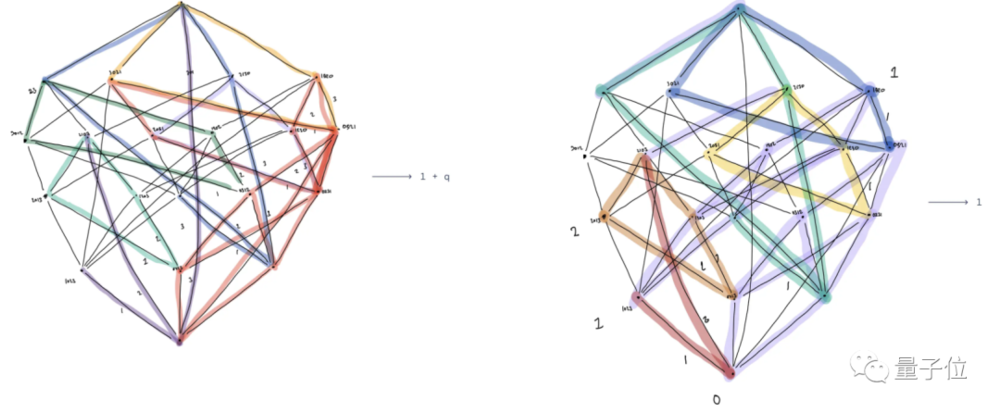
它指出,对称群SN中两个元素的KL多项式可以从它们的无标记Bruhat区间,即一个有向图中计算出来:
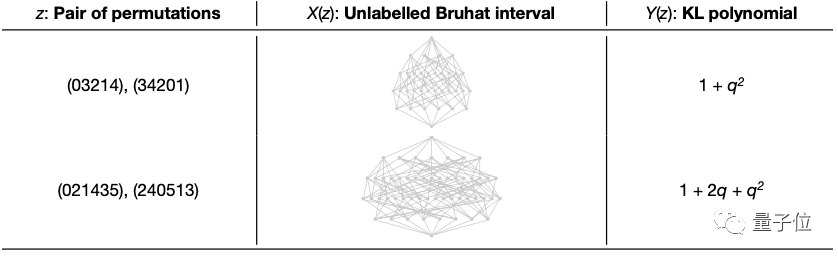
这一猜想已经存在了40年,却只有部分进展。
两位科学家将这个猜想作为初始假设,通过AI中的监督学习模型从Bruhat区间预测KL多项式。
通过计算与确定的归因技术(Attribution Techniques)相关的代表性子图,并分析这些图与原始图的边缘分布,他们发现了进一步的结构证据:
如下图,KL多项式可以通过一个公式直接从超立方体和SN-1部分计算出来。
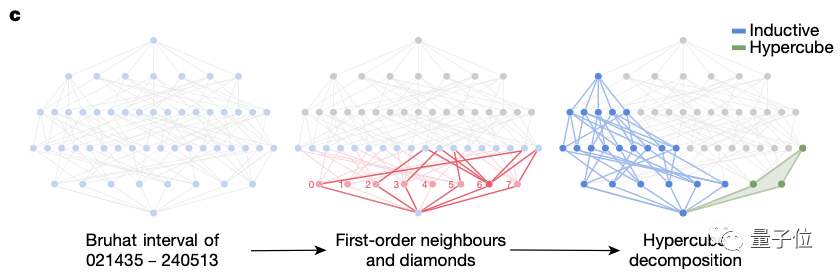
因此,科学家们提出猜想:
一个无标记的Bruhat区间的KL多项式可以用上述的方法,并通过任何超立方体分解(hypercube decomposition)进行计算。
虽然还没有进行严格证明,但目前他们已能在300万个测试例子上验证这一方法。
如果验证成立,那么对称群(Symmetric Group)的组合不变性猜想问题将得到解决。
AI引导数学家直觉
那么整体来说,数学家们到底是怎么与AI合作解决问题的?
或者说AI到底是如何帮助引导数学家的直觉的呢?
简单来说,这篇论文中提出了一种框架,用来快速验证对两个量之间关系的猜想(直觉)是否值得继续探索,如果是的话,则指导如何进一步研究。
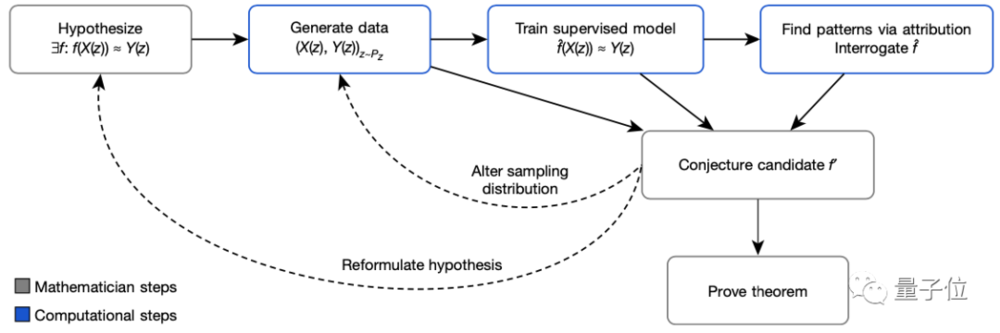
具体来说,先通过监督学习来验证数学对象中的某一结构/模式的假设是存在的。
然后,再使用归因技术来深入理解这些模式。
在这个过程中,AI能够以人类无法比拟的规模输出数据,并从数据中挑选出人类无法检测到的模式。
这正是AI和人类合作与传统的数学研究方法的不同。
其实,数学在很大程度上是一门对关系和模式进行研究的学科。
比如我们小学时就学过的勾股定理,如果将平面上的三角形扩展到八维空间中的900边多面体,还能轻易找到a2+b2=c2的等价形式吗?
答案是:数学家们可以找到,但他们能做的工作量有限。
因为一个人必须评估许多例子,然后才能确定观察到的公式是普遍通用而非偶然。
当然,这篇论文也并不打算创造一个“通用的纯数学助手”,而是让AI去帮助数学家更有效地发现和识别数学中的新模式。
论文的作者之一,牛津大学的Juhász教授表示:
任何可以生成足够大数据集的数学领域都可以使用这种方法,而生物、经济学等领域也将从其中收益。
除了Nature论文外,研究人员还在Arxiv上发布了数学角度解释两个研究的论文,将来会投到合适的数学期刊。
另外还为两个问题提供了Colab代码,让你体验一下与AI合作搞科研是什么感觉。
论文链接:https://www.nature.com/articles/d41586-021-03593-1https://arxiv.org/abs/2111.15323https://arxiv.org/abs/2111.15161
Colab地址:https://colab.research.google.com/github/deepmind/mathematics_conjectures/blob/main/knot_theory.ipynbhttps://colab.research.google.com/github/deepmind/mathematics_conjectures/blob/main/representation_theory.ipynb
参考链接:
[1]https://deepmind.com/blog/article/exploring-the-beauty-of-pure-mathematics-in-novel-ways
[2]https://techcrunch.com/2021/12/01/ai-does-pure-mathematics-and-protein-hallucination/
[3]https://www.nature.com/articles/d41586-021-03593-1
本文来自微信公众号:量子位(ID:QbitAI),作者:博雯、梦晨

