本文来自微信公众号:吴思Lab计算神经科学及类脑计算(ID:gh_0f6ecdddc6a1),作者:吴思课题组(单位:北京大学),头图来自:视觉中国
大家也许在生活中都有这样的烦恼:夏天在外面吃饭时,苍蝇经常会不请自来,围着食物飞来飞去。但要打到它们,即便是高手,用苍蝇拍也很困难。这背后涉及到了一个基本的数学问题,即苍蝇的飞行轨迹似乎符合一种特别的随机运动——莱维飞行(Lévy flight),它使得我们难于预测下一时刻苍蝇的空间位置,从而无法准确出手。本文基于我们最近完成的一份工作[1],介绍了大脑产生莱维飞行的神经计算机制。
一切,从自然界中的随机运动说起
1826年英国植物学家Robert Brown(1773~1858)用显微镜观察悬浮在水中的花粉时发现,花粉粒子在永不停歇地做无规则运动,这一现象也被称作是布朗运动。除此之外,通讯电路中的背景噪声、空气中的尘埃运动等等,在一定条件下,都可以用布朗运动来描述。
我们在下图中展示了一个物体从原点出发,在二维空间中所做的布朗运动的轨迹。看上去很无厘头,不是么?我们很难想象一个生命体在它所在的物理空间中,是这样一种形式的运动。特别是在搜寻食物的时候,显得未免也太不经济了(在一个小的区域过采样很多次)!
其实,早在上世纪七十年代,昆虫和鸟类行为学家Bernd Heinrich在研究蜜蜂采集花蜜时发现,几乎所有的蜜蜂一会儿在一簇花丛打圈,一会儿又呈现一个长距离的飞行[2]。在仔细地分析它们的运动轨迹后,Heinrich发现蜜蜂的运动遵循一种叫做莱维(图中称李维)运动的分布,我们又称之为长尾分布(就像拖了一条长长的尾巴一样,见下图)。
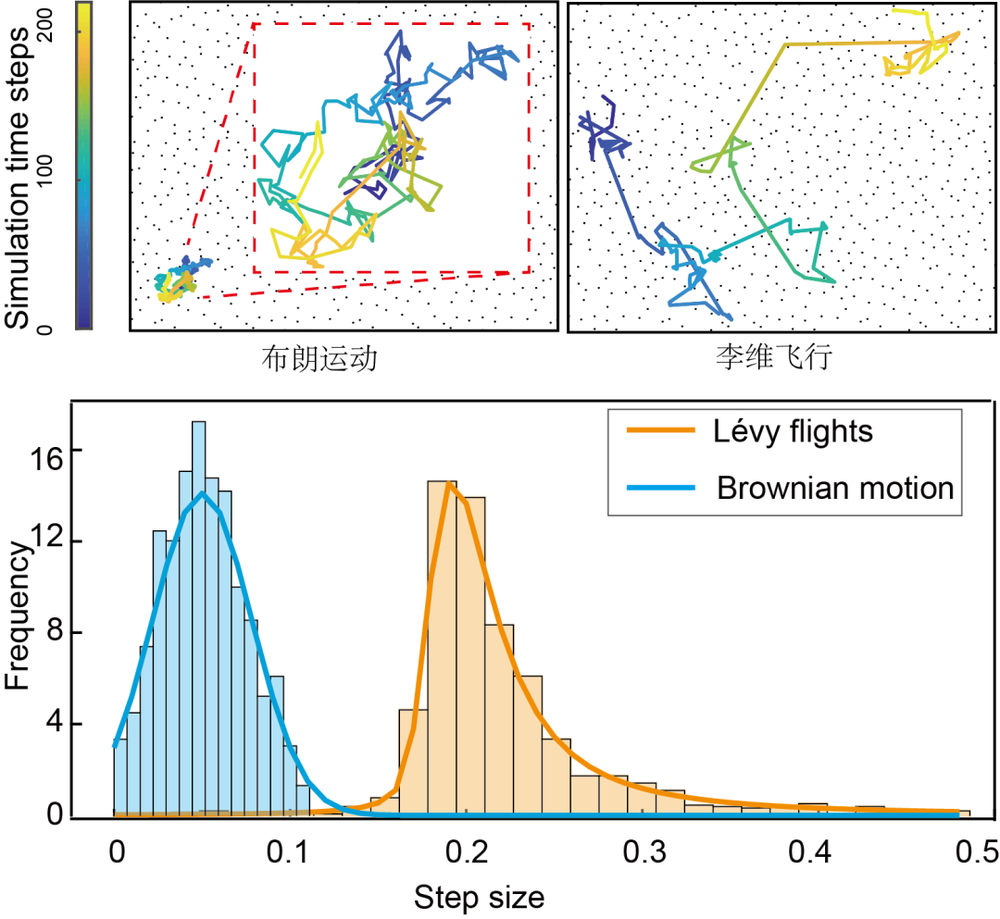
从数学上来讲(花个一分钟看看这个公式以及后面的描述,对下面的理解比较重要哦),不管是布朗运动或者是莱维运动,都可以用一个幂律分布来描述,即p(x)~x-1-α。
其中,-1-α表示幂指数(α本身,又称为莱维指数)。当α比较大的时候,比如α=3,步长取到很大值的概率就会很低;相反地,当α比较小的时(如α=1),步长取一个比较大的值的概率还是相对较高的。数学上稍微严格一点来说,α≥2的时候,由于中心极限定理,上述公式所对应的即是布朗运动。而当0<α<2时,所对应的即是莱维运动。
科学家们在分析的时候经常对上述公式两边取对数,在对数坐标系下,上述公式呈现的就是一个线性表示,而其斜率,也就对应着上述幂律分布的幂次。在Bernd Heinrich之后,科学家们在诸如浮游微型动物[3]、果蝇[4]、信天翁[5]、蜘蛛猴[6]等等诸多不同物种的觅食行为的观察中,都分析得到了类似莱维运动的模态。
2006年,Brockmann等人通过分析美元纸钞在各个银行网点内的流动情况,巧妙地追踪了人类群体在美国各个州的旅行情况,通过解码个体单次的旅行距离,他们也同样也观察到了类似的莱维运动[7]。除了生态学层面上的诸多观测,研究者们还观察到人类在视觉搜索过程中,其眼动距离的分布[8],以及在自由记忆搜寻的过程中,前后两个搜寻出来的物体的名字,其时间间隔分布,均服从莱维运动所示的长尾分布[9]。
进一步地,在大脑活动层面上,研究者们通过功能磁共振成像的方法检测被试在静息状态下的脑活动,发现其血氧信号的强弱起伏,也服从类似的长尾分布[10]。最精细的实验来自于约翰霍普金斯大学的两位研究者Pfeiffer, B. E.和Foster, D. J.于2015年在Science上发表的研究[11]。他们通过多电极阵列记录大鼠在静息状态下的海马体中位置细胞,发现这群细胞的活动所对应的记忆回响(replay)过程,呈现的也是一种莱维飞行。
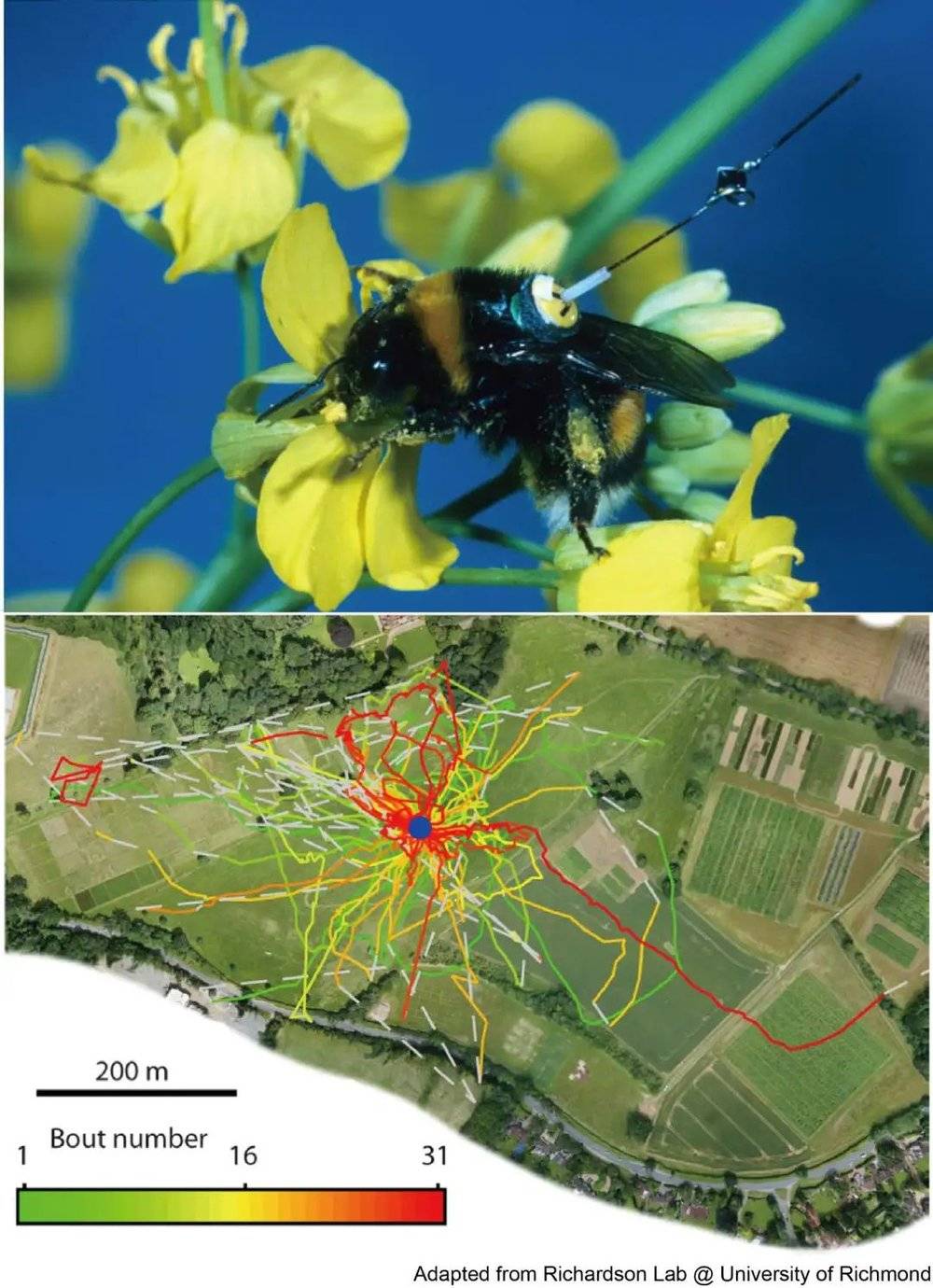
近半个世纪以来,科学家们发现从低等动物到高等动物的觅食行为,从生态学现象到生物体大脑活动状态,从低级认知功能(位置细胞群体的发放模式)到高级认知功能(记忆搜寻)等过程中都有莱维飞行的现象。那么问题来了:产生这种莱维飞行现象背后的神经活动是怎么样的?换句话说,什么样的神经环路,才能够产生莱维飞行呢?我们尝试着从计算建模的角度去探究这个问题。
吸引子网络模型
在计算神经科学领域中,研究者们通常用吸引子网络模型来回答一些大脑结构环路以及功能的一些问题。比如说,我们常用点吸引子(point attractors)来解释联想记忆的发生机制,其中一个比较经典的工作就是大家所熟知的Hopfield network[12];用线吸引子(line attractors)来解释工作记忆以及决策的动力学过程[13];用环吸引子(ring attractor)来解释小鼠头朝向神经元对空间感知的编码[14];用二维的平面吸引子(plane attractor)来解释网格细胞在路径整合中的作用[15]……
既然大脑在加工信息是通过神经环路的动态过程来完成的,而从计算的角度来讲,这样的动态过程,则可以用吸引子网络的动力学过程很好地刻画。那从计算的角度来看,一个自然而然的科学问题则是,吸引子网络如何才能产生莱维飞行。
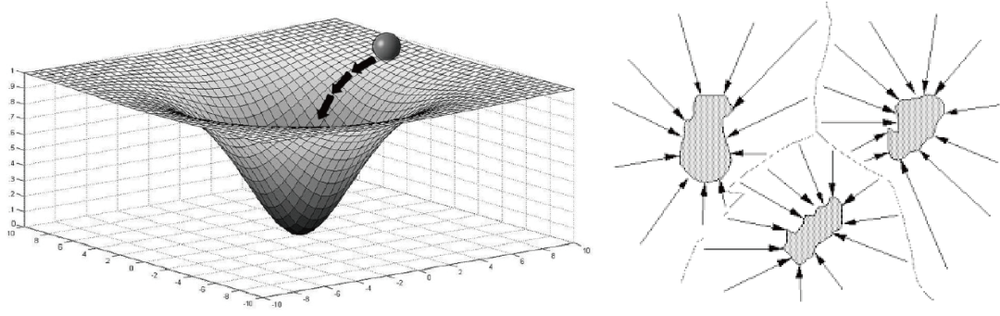
为了回答上述的问题,我们探究在一个具体的计算模型下,网络状态如何产生莱维飞行。而这个网络就是今天的主角:二维连续吸引子网络。
二维连续吸引子网络模型常常被用来刻画对二维连续信息的表征。比如哺乳动物大脑海马体中对二维空间位置的表征,就可以很好地用一个二维的连续吸引子刻画。如下图所示,蓝色的星星表示外界的刺激,可以认为是大鼠在二维空间中移动时的视觉输入,而黑色的波包,则表示大鼠海马体中对位置表征的神经元群体反应。图中的每个空心圆圈,代表着一个个的神经元,它们均匀地散落在二维的空间中,并且相互之间有着连接。
当视觉刺激输入变化时,波包的位置也随即跟着外界刺激而变化。波包的移动在这个二维空间中是连续变化的,也就是连续吸引子网络中“连续”的含义所在。值得注意的是,外界刺激撤去的时候,波包能够稳定在刚刚刺激撤掉的位置,这也就是“吸引子”所代表的含义。总的来说,连续吸引子网络模型可以有以下的特点:在低维特征表示空间中,每一个位置上的波包其自身都是一个稳定点,而且不同位置上的波包能够在这个低维空间中连续迁移。

为了使大家能更加清楚地了解网络模型是如何工作的,我们接下来稍微讲点数学。我们所展示的二维连续吸引子的网络动力学可以表示如下[16]:
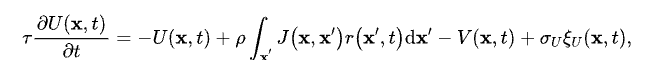
其中,x=(x1, x2)表示每个神经元编码的一个二元特征,用其在二维空间中的位置表示;-U(x, t)为一个漏电项,当没有外界输入的时候,神经元的反应会指数衰减;J(x, x')则为神经元之间的连接强度,其大小随着神经元之间的相对距离而递减;-V(x, t)则是神经元的适应(adaptation)机制,下文中我们会着重讲,而最后一项σUξU(x, t)则代表的是神经元层面的噪声。
这个动力学系统使得网络的稳定状态形成中心坐标连续变化的一系列局部波包。为了实现在二维表征空间中的莱维飞行,一个最重要的机制就是使得网络状态在二维空间中自主运动,并且其运动能够展现出时而局部震动、时而长距离朝一个方向前进。如果有某种机制能够使得网络在这两个状态下切换,我们自然就能够实现莱维飞行啦!
为了实现网络状态的自主运动,我们可以考虑神经元适应机制(neural adaptation),具体来说,叫做发放频率适应(spike frequency adaptation,SFA)。注意哦,我们这里讲的是自主运动,而非外界刺激变化带来的运动。从生物上来讲,神经元适应可以理解为,当给一个神经元直流电输入,从而引起神经元发放时,其自身的放电并不会维持在一个不变的水平,相反的,其放电频率会随着时间不断减弱。
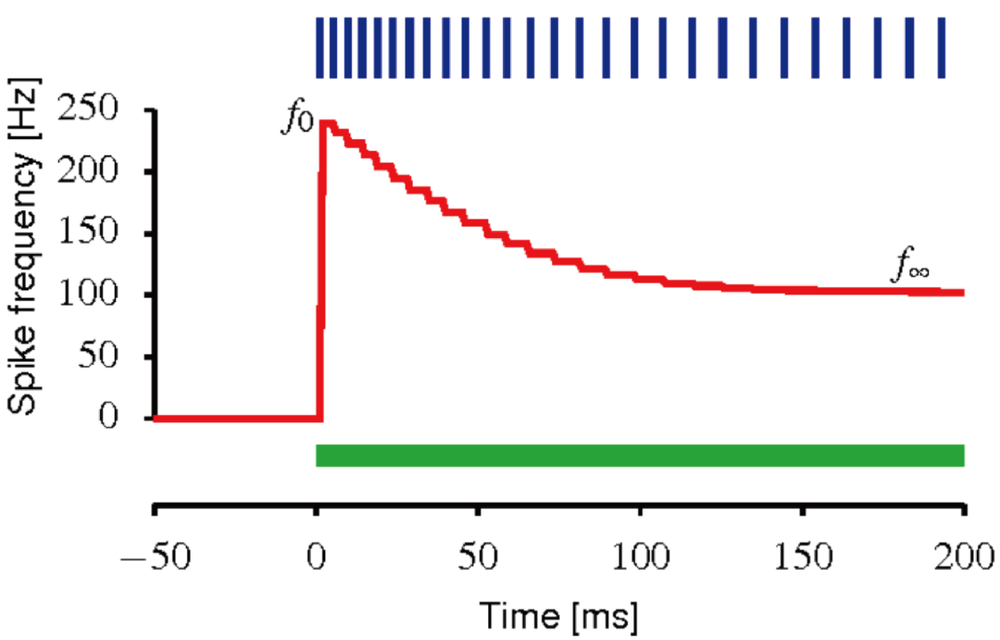
我们对上述的二维吸引子网络中的每个神经元加上SFA,其动力学如下:
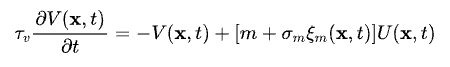
其中,m为SFA的强度,而σmξm(x, t)则是独立于连续吸引子网络中神经元层面的另一个噪声项。从上述两个公式可以看出,SFA的作用机理相当于引入了一个负反馈机制,使得神经元越兴奋,则其越容易被自身的SFA所抑制,从而降(明)低(哲)反(保)应(身)。
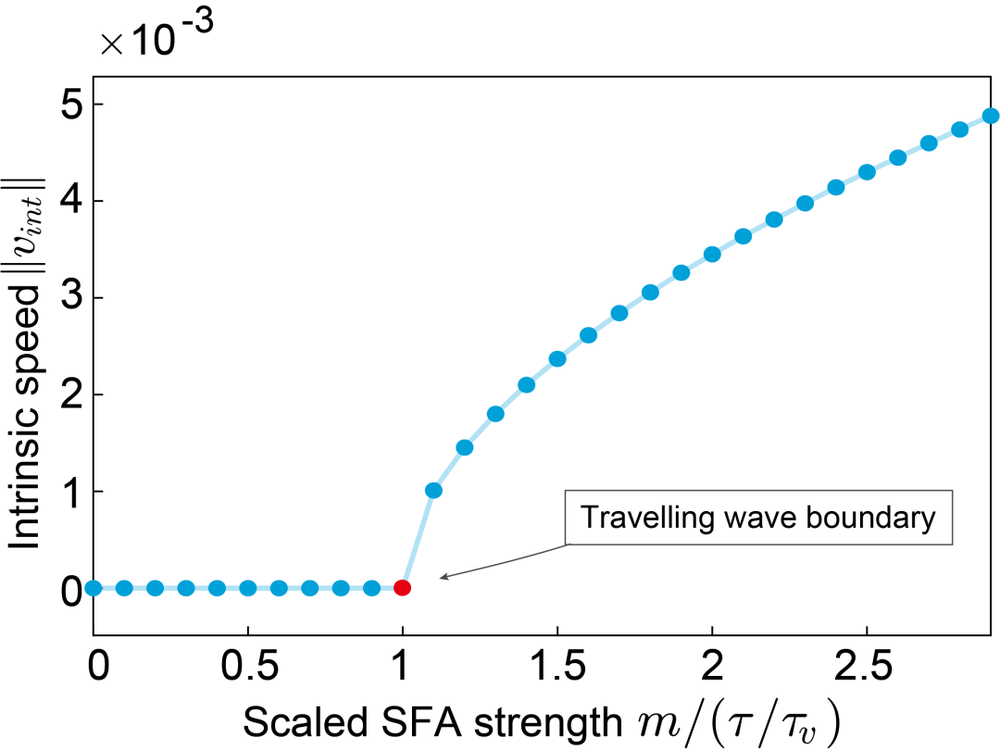
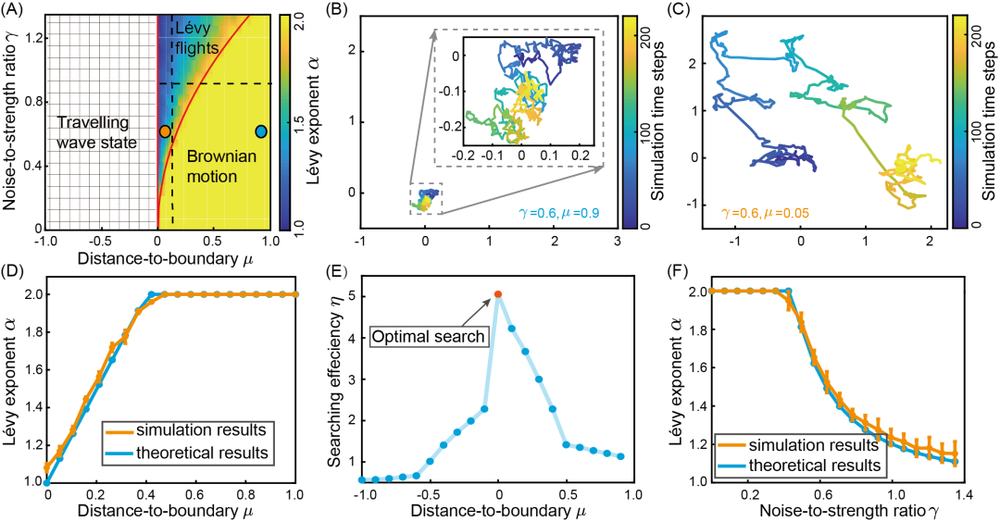
我们回到二维的连续吸引子网络,假设波包稳定在某个位置,但是由于SFA的负反馈机制,网络会倾向于把波包往某个方向推出去。而当抑制强到一定程度时,波包就能够在二维空间里面运动起来,产生运动波(travelling wave)[17]。我们可以用一些数学分析的技巧,理论性地解出抑制强度和波包运动速度的关系。
可以由下图看到,当抑制强度m小于τ/τv时,网络状态并不会在二维空间中做迁移,也就是说,波包要么稳定在某个位置不动,要么随着噪声项在局部空间中做布朗运动。而当抑制强度m大于τ/τv时,波包所表示的网络状态就有一个内在的速度(intrinsic speed),能够在二维空间中做长距离的前进。
设想一下,如果我们把SFA的抑制强度设置在这个边界上,由于SFA上噪声的影响,抑制强度则会时而小于边界值,时而大于边界值,这样一来,网络波包时而做局部运动,时而长距离的前进,这也就符合我们在一开始说的莱维飞行的特点了!
从上面的动力学系统出发,经过一系列的理论推导(此处省略一万字),我们可以得到关于波包中心位置z的变化方程:
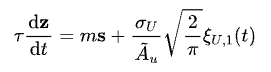
其中s则是网络状态本身的波包位置以及SFA所带来的虚拟波包位置之间的距离差,其本身也是一个动力学方程,写为:
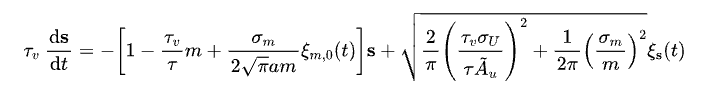
看到这里同学们可能已经晕了,但是没关系,如果跳过,仍然可以在下文抓住重点!我们此处再省略一万字,直接把上述关于z和s的方程的解告诉大家,也就是我们秘密的揭晓时刻:
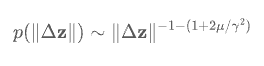
其中μ=1-mτv/τ描述了SFA强度到边界的距离,而γ=σm/(2am√π)为噪声的相对方差。我们设α=1+2μ/γ2,当μ和γ的取值在一定范围内时,我们就能使得0<α<2,从而实现我们在一开始说的莱维飞行;而除了实现二维连续吸引子上的莱维飞行,我们调整μ和γ的取值,还可以实现二维连续吸引子网络上诸如布朗运动、运动波等等有趣的现象。
(那些跳过数学细节的同学们,此时可以回到文章中来了◠‿◠)
我们尝试着从神经动力学模型去探讨了大脑产生莱维飞行可能的动力学机制,总的来说,通过神经元发放频率适应(spike frequency adaptation)这样一种内在而简单的机制,在连续吸引子网络模型中产生了莱维飞行。并且用数学分析的方法,透彻地解释了产生莱维飞行背后的动力学过程,而且刻画了产生不同动态模式(诸如莱维飞行,布朗运动以及运动波等)下的参数区间。最后,我们给大家展示一个有趣的例子,来佐证我们提出的模型。
记忆搜寻任务中的莱维飞行
来自康涅狄格大学的Rhodes和Turvey使用自由记忆检索任务对人类认知中的莱维飞行进行了第一次研究[8]。在他们的实验中,八名参与者被要求在大约20分钟的时间内尽可能多地(不重复)口头回忆动物名称,并记录连续回忆之间的时间间隔。有趣的是,他们发现回忆起的名称个数随时间的增加并不是均匀的,而是由穿插着短间隔爆发组成的指数增长。
总的来说,回忆两个名称之间的时间间隔服从莱维分布,从而使得该过程可以用莱维飞行来描述。并且他们测得不同参与者的莱维指数分布的范围为0.37<α<0.98。在这里,我们展示了这种自由记忆检索的莱维飞行行为可以通过对语义图的随机搜索来描述,该语义图可以由带有SFA的吸引子网络来建模。
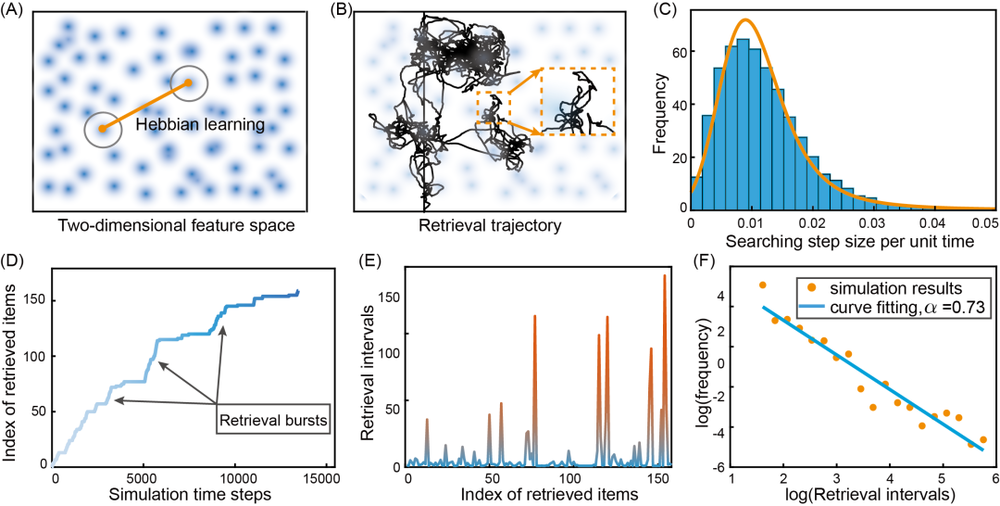
具体来说,我们构建了一个类似Hopfield的吸引子网络,其中每个记忆项都由一个随机分布在二维特征空间中的局部神经群体表示。神经元连接由Hebbian学习确定,因此每个记忆项都被编码为网络的吸引子(见下图A)。成功检索一个记忆项意味着网络状态落入相应的吸引子。注意啦,在这样的网络中,静止状态不再像CANN那样形成连续的中心稳定性流形。
即便如此,如果自适应强度足够强,SFA仍然可以驱动网络状态在不同的吸引子之间传播。因此,当SFA强度的均值和方差设置适当时,网络状态会在特征空间中的局部布朗运动和跳远运动之间间歇性切换,表现出莱维飞行的特征(见下图B&C)。
为了重现实验结果,我们计算了连续检索之间的间隔,这些间隔是通过网络状态从一个吸引子传播到另一个吸引子的持续时间来衡量的。下图D显示检索项目的数量与模拟时间成对数比例,并且记忆条目在突发中间歇性地被召回,这与实验结果非常吻合。
进一步的分析表明,长的检索间隔被非常短的间隔爆发打断,长间隔的长度随时间呈指数增长(见下图E),这与实验上所观测到的人类行为非常吻合。我们还通过检索间隔的对数-对数频率分布的线性拟合来计算莱维指数,为α=0.73(见下图F),落在了实验结果测得的0.37<α<0.98范围内。
总结来说,我们的工作研究了大脑产生莱维飞行的神经机制,并详细研究了其实现:从具有一般神经特征的神经环路模型开始,我们推导了吸引子空间中网络状态的动力学,并证明它具有莱维飞行的特征。此外,我们还利用该模型模拟了与莱维飞行相关的一些认知功能。
结束语
上面介绍了神经系统产生莱维飞行的一种可能机制。不过遗憾的是,虽然我们知道了苍蝇为什么会这样飞行,这对我们提高打苍蝇的技艺的帮助还是非常有限,因为我们不能阻止苍蝇做莱维飞行,因为莱维飞行本身代表的是一种很难预测的随机运动。
那么对生活中我们大脑的自主活动,是否可以利用其背后的神经机制来提高技艺呢?想必大家同学聚会的时候或多或少都玩过“逛三园”的游戏:一群人围成一圈,从其中一个人说逛什么园(植物园、动物园和蔬菜园),如动物园,其他人就要说与那些园有关的事物,如猴子、狮子、大象,如果说错和说不出来者,某个人反应太慢,没有说出相应的东西,或者说出的东西与前面人重复,则就应受惩罚。
整个过程对应到认知科学上,其实就是一个记忆搜寻的任务,需要每个人从自己的记忆空间中搜索出前面所有人没有说出的事物。有趣的是,我们常常会看到某些人总是输,而某些人总是给人感觉很机灵,永远都能想到别人没有说过的词。今天的文章就交给那些常输之人一个小技巧,在记忆搜索时多做莱维飞行,或许可以让你从此成为逛三园的牛人。
编者的话:该公众号文章是基于我们课题组在今年的人工智能顶会NeurIPS上的一篇相关工作的科普介绍,由吉子龙、褚天昊、董行思共同撰写。之所以取了这么一个涉嫌标题党的题目是因为该研究真的是起源于去年差不多同一时期的一篇公众号文章。具体细节记不得了,文章题目大概是“苍蝇为什么难打”,内容则是介绍了苍蝇的飞行轨迹是莱维飞行,因此难于预测。当时就觉得特别有趣,想破译其背后的神经机制,随后经过组里讨论,就确定了这个研究课题。感谢董行思和褚天昊(共同一作)、吉子龙(共同通讯)的辛勤付出,在这么短时间就完成了这篇高质量工作,也祝贺他们的文章被NeurIPS接受!
参考文献
[1] Xingsi Dong, Tianhao Chu, Tiejun Huang, Zilong Ji* and Si Wu* (2021). Noisy Adaptation Generates Lévy Flights in Attractor Neural Networks. NeurIPS 2021 (accepted).
[2] Heinrich, B. (1979). Resource heterogeneity and patterns of movement in foraging bumblebees. Oecologia, 40(3), 235-245.
[3] M Levandowsky, J Klafter and BS White. “Swimming behavior and chemosensory responses in the protistan microzooplankton as a function of the hydrodynamic regime”. Bulletin of Marine Science,1988, 43(3): 758–763.
[4] Blaine J Cole. “Fractal time in animal behaviour: the movement activity of Drosophila”. Animal Behaviour, 1995, 50(5): 1317–1324.
[5] Gandhimohan M Viswanathan, V Afanasyev, SV Buldyrev et al. “Lévy flight search patterns of wandering albatrosses”. Nature, 1996, 381(6581): 413–415.
[6] Gabriel Ramos-Fernández, José L Mateos, Octavio Miramontes et al. “Lévy walk patterns in the foraging movements of spider monkeys (Ateles geoffroyi)”. Behavioral ecology and Sociobiology, 2004, 55(3): 223–230.
[7] Brockmann, D., Hufnagel, L., & Geisel, T. (2006). The scaling laws of human travel. Nature, 439(7075), 462-465.
[8] Brockmann, D., & Geisel, T. (2000). The ecology of gaze shifts. Neurocomputing, 32, 643-650.
[9] Rhodes, T., & Turvey, M. T. (2007). Human memory retrieval as Lévy foraging. Physica A: Statistical Mechanics and its Applications, 385(1), 255-260.
[10] Costa, T., Boccignone, G., Cauda, F., & Ferraro, M. (2016). The foraging brain: evidence of Lévy dynamics in brain networks. PloS one, 11(9), e0161702.
[11] Pfeiffer, B. E., & Foster, D. J. (2015). Autoassociative dynamics in the generation of sequences of hippocampal place cells. Science, 349(6244), 180-183.
[12] Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proceedings of the national academy of sciences, 79(8), 2554-2558.
[13] Mante, V., Sussillo, D., Shenoy, K. V., & Newsome, W. T. (2013). Context-dependent computation by recurrent dynamics in prefrontal cortex. nature, 503(7474), 78-84.
[14] Zhang, K. (1996). Representation of spatial orientation by the intrinsic dynamics of the head-direction cell ensemble: a theory. Journal of Neuroscience, 16(6), 2112-2126.
[15] McNaughton, B. L., Battaglia, F. P., Jensen, O., Moser, E. I., & Moser, M. B. (2006). Path integration and the neural basis of the'cognitive map'. Nature Reviews Neuroscience, 7(8), 663-678.
[16] Wu, S., Wong, K. M., Fung, C. A., Mi, Y., & Zhang, W. (2016). Continuous attractor neural networks: candidate of a canonical model for neural information representation. F1000Research, 5.
[17] Mi, Y., Fung, C. C., Wong, M. K. Y., Wu, S. (2014). Spike frequency adaptation implements anticipative tracking in continuous attractor neural networks. NeurIPS, 505.
本文来自微信公众号:吴思Lab计算神经科学及类脑计算(ID:gh_0f6ecdddc6a1),作者:吴思课题组

