本文选自《物理》2021年第9期，首发于微信公众号：中国物理学会期刊网（ID：cpsjournals），作者：葛墨林（南开大学陈省身数学研究所），题图来自：视觉中国


杨振宁先生的一系列物理文章，几乎就是20世纪下半叶理论物理的发展史，考虑到对物理发展的影响，可以用“伟大”二字形容。


已有许多书刊文章对杨先生科学成就进行介绍。如果试图从后学者角度扼要概括杨先生的学术思想，大胆评述如下：


基本物理思想：


  • 对称性支配自然，真实的物理对称破缺。

  • 由物理推动做研究。以实验为依据提出新方向，解决难题。

  • 物理是猜测和实验的学问。

  • 物理与数学密切结合。


风格：


  • 宁拙勿巧，宁朴勿华。

  • 3P：Perception(洞察力)，Persistence(坚持力)，Power(强有力)。

  • “文章千古事，得失寸心知”。


戴森(F. Dyson)在《鸟和青蛙》中写道：杨振宁高高地飞翔在诸多小问题构成的热带雨林之上，我们中绝大多数人在这些小问题里耗尽了一生的时光。


本文目的一是尽可能用物理研究生的语言解释杨先生的工作，二是简要介绍多年来国际物理界对杨先生工作的发展。接下来本文将分以下四部分对杨先生的重要科学成就进行介绍。主要文献参看《杨振宁论文选集，1945—1980》，不再另列文献目录：


  • 对称及破缺：杨先生是粒子物理理论奠基人之一，包括宇称不守恒(与李政道先生合作)，获诺贝尔物理学奖。以弱作用P-不守恒为代表的基本粒子一系列分立对称性及破缺。

  • Yang—Mills(YM)场：革命性成果。

  • Yang—Baxter方程(YBE)：开拓非线性可积性的数学物理新领域。

  • 统计物理核心问题及预言(包括凝聚态理论创新)。


1. 以弱作用P-不守恒为代表的基本粒子分立对称性及破缺


1.1 角分布理论


在文章“On the Angular Distribution in Nuclear Reactions and Coincidence Measurements”(Phys. Rev.，1948，74：764)中，设非极化的两粒子碰撞：



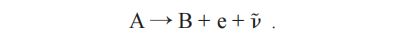
电子和中微子的角关联是cosθ 的多项式，最高幂次为K+1，对允许跃迁 K = 0，而对第一禁戒跃迁 K = 1。


1.2 弱作用中宇称不守恒及中微子二分量理论


在文章“Parity Nonconservation and Two-Component Theory of the Neutrino”(with T. D. Lee，Phys. Rev.，1957，105：1671)中，由狄拉克理论，β衰变哈密顿量应包括P，A，V，…，假定只有A，V，即中微子只有两分量，则狄拉克方程为(ℏ = c = 1)



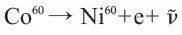对(实验为反应)，反应几率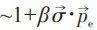，即1+βcosθ，当宇称变换，则cosθ → -cosθ。


实验(吴健雄先生等)证实 β ≠ 0，即宇称不守恒。在此后，杨先生和李先生有一系列文章讨论其他分立变换不守恒问题。值得注意的是，当时由于K介子衰变的θ -τ问题，引起怀疑P不守恒的可能性。但困难在于如何提出实验检验。杨先生有关角分布的长期功底促成了他提出用角分布检验弱作用中P是否守恒的问题。


为了以后说明问题方便，扼要介绍P(宇称)，T(时间反演)，C(电荷共轭)变换：


设狄拉克波函数取：


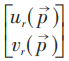
熟知当自由粒子作用量洛伦兹不变时，CPT定理成立。有了以上关系，容易理解杨先生和李先生一系列文章中有关分立变换在基本粒子理论中的应用，包括与李政道先生合作的工作。


  • 引入推广的电荷共轭 G = C exp(iπI2)，I2：同位旋四维表示。

  • β衰变，超子、介子衰变中P不守恒的实验检验。

  • T反演和C(电荷共轭)不守恒的猜测。


我们着重介绍的是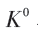与。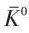


衰变中CP不变性破坏的唯象分析(与吴大峻先生合作)，它成为以后这方面一系列实验的指导性文献。


K -介子有奇异量子数：



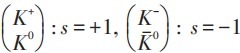
CP变换的本征态：





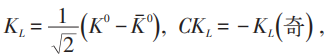
KL 的寿命大约是KS 寿命的500倍：



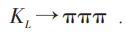
当处于S态时，CP=-1，故CP守恒。但实验发现存在衰变：



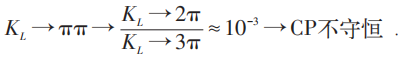
在合作文章中吴—杨引入了唯象参数ϵ，指导了以后的实验工作。


2. 引入杨—米尔斯场，改变了物理研究的面貌


回忆电磁场：



由电动力学：



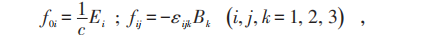
以后取c =1，麦克斯韦方程(在无外源时)：



以及恒为0的Bianchi恒等式：



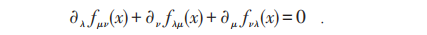
它等价于：



其中ϵμνρτ为四维全反对称张量。


由于Bianchi恒等式，如果*fμν(x)=fμν(x)，i.e.  Ei = Bi，则称为自对偶(self dual，SD)。显然如果电磁场自对偶，由于Bianchi恒等式，则自然满足场方程∂νfμν(x)=0。


电磁场是规范场，做规范变换时场不变。即电磁势Aμ(x )做如下变换时，fμν(x)不变。



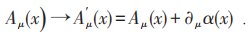
但势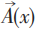有单独物理效应(量子力学需要势)，它已为Aharonov—Bohm效应实验证实。杨先生特别重视Tonomura的实验。

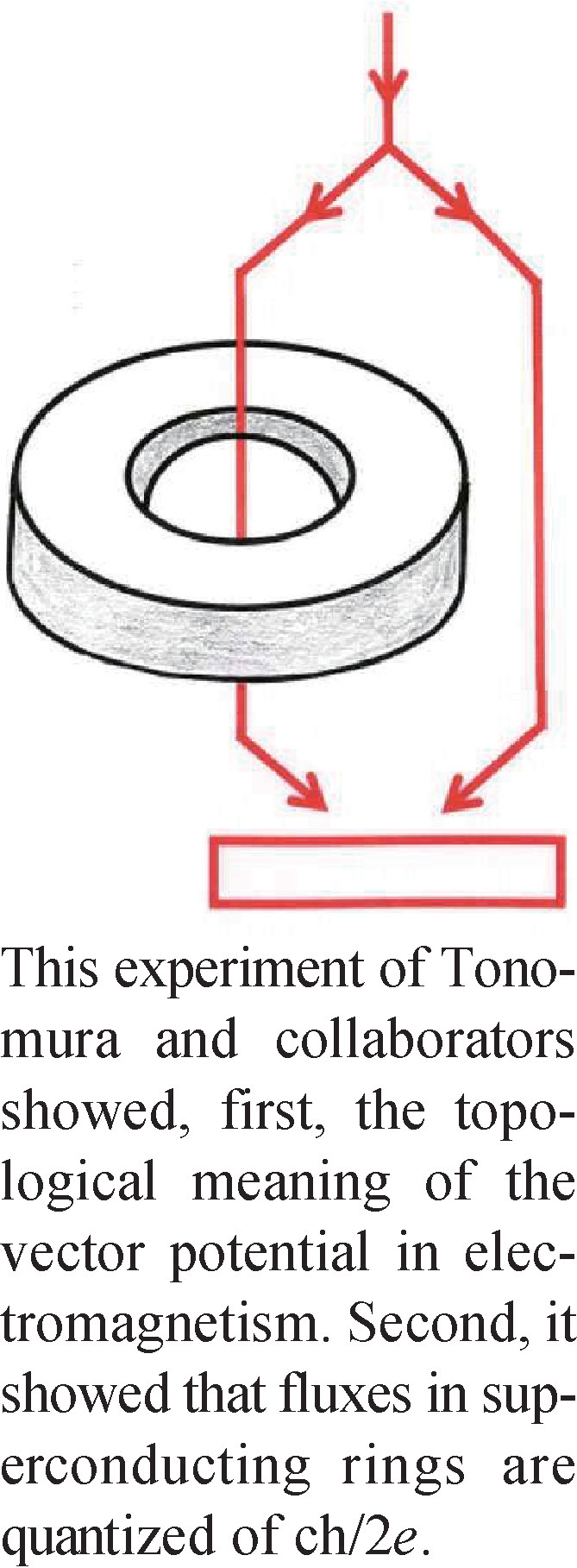
下图选自杨振宁先生报告：Topology and Guage Theory in Physics。
下图选自杨振宁先生报告：Topology and Guage Theory in Physics。


物理学中的相互作用是通过规范场传递的。电磁作用通过光子传递，但光子本身并不带有电荷e，熟知电磁作用时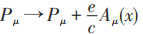，即。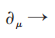


电磁作用与电流耦合即为：



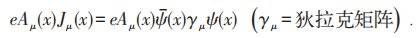
在物理确认质子(p)和中子(n)组成原子核后，它们不同的电荷态用同位旋描述，即：



同位旋(isospin)：


为2×2矩阵，即：


描述具有同位旋两分量粒子间相互作用，杨先生引入了新的规范场，即Yang—Mills(YM)场“Conservation of Isotopic Spin and Isotopic Gauge Invariance” (with R. L. Mills， Phys. Rev.， 1954， 96：191)，并建立包括拉格朗日量不变性和量子化方案。电磁场规范场是阿贝尔的，而YM属于非阿贝尔的SU(2)。其后被许多学者推广到大量非阿贝尔群(尤其是SU(3)，改变了物理的面貌)。


引入的YM规范势以李代数的矩阵表示为基：



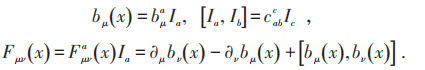
规范变换为：



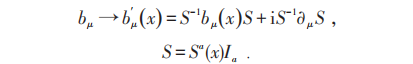
对SU(2)：



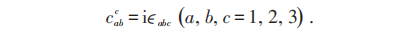
三维全反对称张量ϵabc就是同位旋矢量的叉乘。相应Bianchi恒等式为：



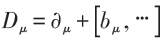为包含YM场的平移算子。


现在物理界已普遍接受群论方法。但在六十七年前杨先生将非阿贝尔规范场引入物理，它传递“非阿贝尔相互作用”是大胆而有开创性的事，它引发了物理学革命性进展，同时也引发数学(方程、几何、拓扑等)的革命性进展。YM传递互作用时，应是短程作用，这要求其规范场粒子有质量，同时这种粒子有三个分量，其正、负分量应带有作用荷。这在当时从电磁场角度是难以理解的，但以后都被物理学家们解决。例如泡利就曾对质量问题进行了质问，后来被Higgs机制所解决。


正如杨先生在“Conservation of Isotopic Spinand Isotopic Gauge Invariance” 中强调的，在电磁场中存在不变性，如电荷守恒，由电磁规范势传递互作用。YM 场就是将这一规范不变性推广到同位旋规范不变性(并导致YM场方程)，它是非线性的，自身就提供了源，因而引起同其他场的新型互作用。


YM 理论以后向两个方向发展：数学的和物理的。


经典YM方程 DνFμν(x) = 0 求解，引发物理与数学中陈省身示性类，非线性系统拓扑性质的交叉，许多著名数学家、物理学家卷入其中。


量子化后，Gell-man引入SU(3)导致QCD(量子色动力学)发展，而 SU(2)× U(1) +Higgs场导致了标准模型等等一系列粒子物理中的巨大成就引发了7位诺贝尔物理学奖。


2.1 自对偶YM(SDYM)场方程的解


注意到Bianchi等式可写为另一种形式。定义：


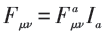
的对偶(Dual)形式：



则Bianchi等式可写为Dν*Fμν=0。如果取自对偶Fμν=*Fμν，则自然满足：DνFμν=0，称为自对偶解(SDYM解)，此时YM场能量可表示为：



如考虑到引入自作用常数g，对SU(2)，其中：



即“带同位旋”的电场和磁场。易证SDYM相应的能量最低，系统稳定，并且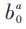实际起了类似Higgs场的作用。


SDYM一种典型的静态解是磁单极解(monopole)。例如：若选取Ansatz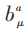，取下面形式，其中设同位旋空间与三维球坐标同步：



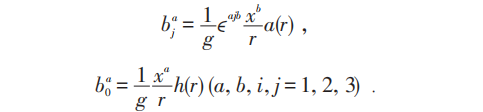
则SD条件得到孤子解：



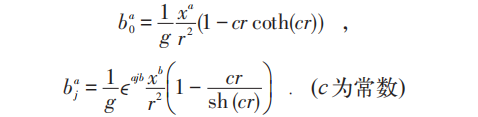
它在r=0时有限，而系统能量E=Em=4π/g2，此时对应的拓扑类为第一陈类(Chern Class)：



这是典型的无源SDYM场的磁单极解，对于n=1，渐近条件为：



2.2 YM的瞬子群


YM场的作用量：



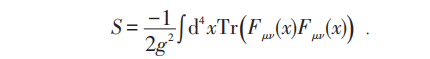
由于：



注意：



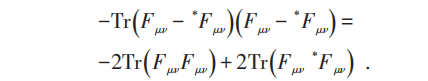
可知作用量：



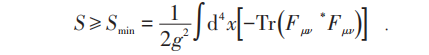
易知SDYM对应极小：



它对应第二陈类：



事实上将Fμν(x)用bμ(x)表示的形式代入，得：



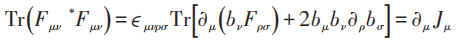
如果要求三维球中r → ∞时，Fμν → 0，相应的：



则：



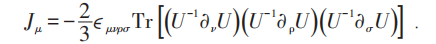
相应的同伦群为：



在讨论瞬子解(Instanton)时，为方便取μ=1, 2, 3, 4, ( x4=ict )，寻求 x 2 = x12 + x22 + x32 + x42 在无穷远处渐近形式：



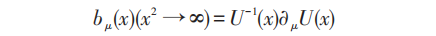
的Ansatz形式的解：



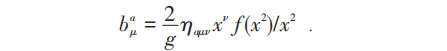
边界条件为f (|x|→0)=1，f(|x|→∞)=cx2，c 为常数，ηaμν为't Hooft记号：



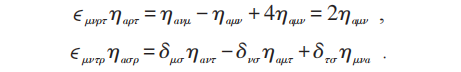
可得瞬子解(明显形式见下节)。


2.3 R-规范杨振宁方程


由于 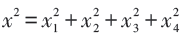，引入复坐标：



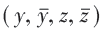
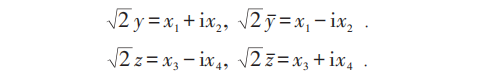
相应的：



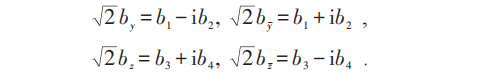
则SD条件导致：



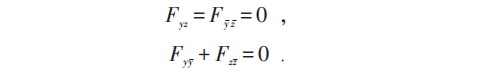
于是可令：



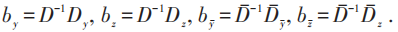
其中：



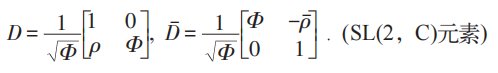
从而SD条件导致(下标表示微商)：



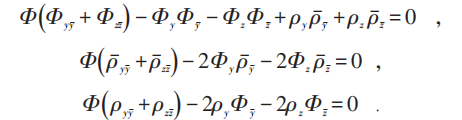
三者结合即为R-规范杨振宁方程。引入记号：



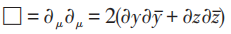
上述三个方程可表为：



后两者，类似柯西—黎曼条件向四维的推广。


上述方程有一明显的解：



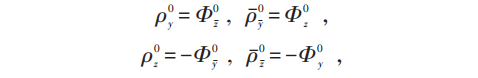
它们的可积条件为：



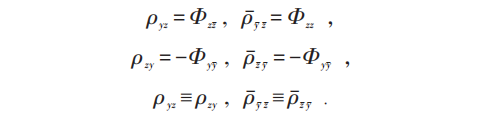
于是得到：



在四维欧氏空间中，其解为：



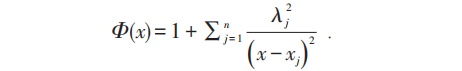
λ1,λ2⋯λn 为参数，它给出了't Hooft的瞬子解：



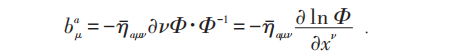
事实上SDYM的R-规范场方程包括了已发现的SDYM的各种孤子解，另外，以后有人证明SDYM方程是个母(mother)方程，由它可推出许多已知孤子方程(Ablowitz等)。


2.4 吴—杨磁单极势


狄拉克磁单极是引入矢量势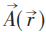，它产生的磁场。


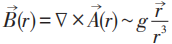最简单的考虑是把磁偶子当中一个极移动到无穷远，这样有限范围面内中心处呈现了一个磁单极子，但问题是这就引起一根弦，它是有奇异性的，为避免这种奇异性，吴大峻先生和杨振宁先生在“Dirac monopole without strings: monopole Harmonics”中引入：




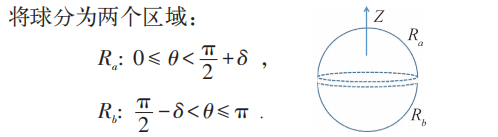
即把两个半球扣起来，形成坐标邻域。取Ar=Aθ=0：


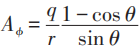
取球的上部Ra，如图：


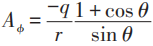
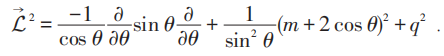
本征态：



s0依赖于q 的取值。故波函数为：



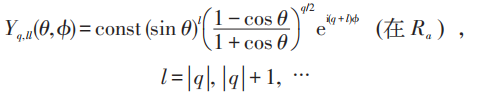
例如q=1/2时：


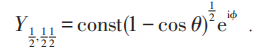
设想一个氢原子中心具有ze电荷，如空间几何结构等效为吴—杨磁单极时，则其基态能量为：



2.5 经典YM方程求解


经典YM方程求解问题一时成为数学物理的热点研究领域，'tHooft得到Higgs势与YM作用的磁单极，'t Hooft—Polyakov得到磁单极，瞬子解。吴大峻与杨振宁给出规范场积分形式与纤维丛的联系，尤其与拓扑(陈省身示性类)的联系，推动了物理与拓扑的结合。


Atiyah(英国皇家学会前会长)与Ward利用twister理论分析了SDYM构造的几何特征，给出了多个磁单极和瞬子解的几何框架。包括Corrigan等人，Belavin，Zhvonov，Prasad，Witten等等都做出了创造性工作。


乔玲丽在杨先生R-gauge基础上建立了J-形式SDYM的可积框架，并与吴詠时、葛墨林合作证明了可积性，从而把YM与推广的Lax-pair可积系统联系起来，并引入黎曼—希尔伯特变换讨论了SDYM的loop代数。


在YM方面，徐湛和张礼先生等做出优秀工作，被称为Chinese Magic(中国魔术)，为人所熟知。


至今，仍留下不少未解决的难题，尚待解决。


2.6 基于YM的量子场论


基于YM发展起来的量子场论更取得了耀眼的成就。包括Weinberg(Glashow，Salam)创造的标准模型到今天仍是高能物理最关注的课题方向。它主要是考虑SU(2)×U(1)理论，并引入Higgs场提供质量。


其中SU(2)的第三分量与U(1)混合角为Weinberg角时，出现无电荷粒子即光子与有质量的Z0，而荷电分量为W±粒子。W±，Z0被实验所发现(包括丁肇中先生贡献)。


在Gell-man提出八重法(SU(3))后，YM推广到更复杂的半单李代数，典型的形成色动力学(QCD)，几乎统治了强子物理。


费曼的路径积分(path integral quantization)的生成泛函：



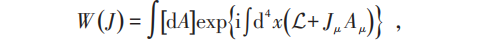
其中A为规范势：

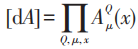
Q是李代数指标。


Faddeev—Popov等把积分内指数项表示为规范固定项。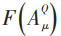


与规范补偿项(与鬼场Ca(x ))有关：



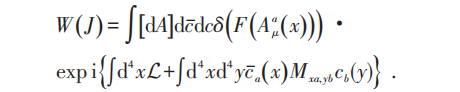
可选择任意规范，例如朗道规范：


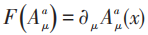
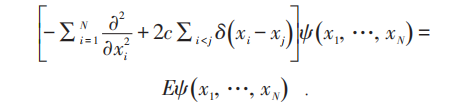
杨先生首先考虑玻色子，其后与杨振平先生解决了费米子情况。


玻色子波函数：



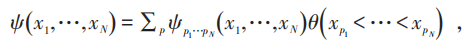
上式右端对所有排列取和，共有N !项。由于玻色子全同性：



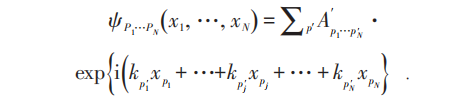
周期边界条件时，Bethe Anstatz关系导致：



系统的动量、能量为：



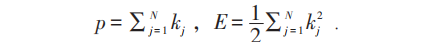
费米子情况与玻色子不同。玻色子系统坐标和动量是在同一置换下排列的，但对费米子两者不同，置换分别为：



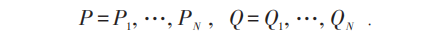
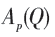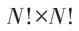它们为两种排列，故应对两种排列分别求和，元素共有：个，于是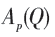应写为矩阵形式：



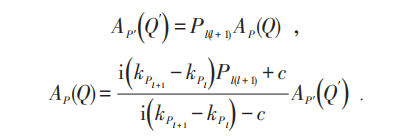
值得强调的是，一维 δ -函数作用势模型与(孤子方程)非线性薛定谔方程(NSE)等价。NSE的哈密顿量为(H. B. Thacker)：



上述结果是必然的，因为粒子数守恒时场论和多体问题是一致的。其后，L. D. Faddeev证明NSE是XXX链模型的连续极限。


特别需要关注的是，杨先生引入的算子(表为矩阵)Yij，以后通用记号记为Rij，它虽然最早是对δ-函数作用势引入的，但它的涵义远远超过了这个模型。事实上，它揭示了一大类精确可解的可积非线性模型的共同特点。其后，发展成数学物理主导方向，至今不衰。


如上述，杨先生文章中用 Ri, i+1 表示，它 是 N × N 矩 阵 的 矩 阵 元 ， 在 原 始 文 献 “Some Exact Results for the Many-Body Problem in One Dimension with Repulsive Delta-Function Interaction”中，熟知置换群P 满足：



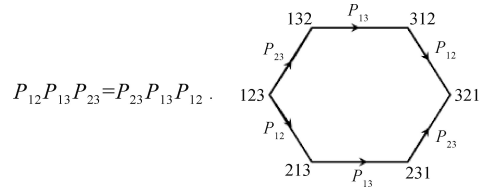
其中下标标示全同粒子。


表示从两个不同途径置换都会从123排列变为321排列。杨先生引入的关系可写为：



其中ki 为第i 个粒子的动量(ℏ=1)，一般记为杨—Baxter方程(YBE)：



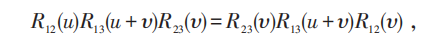
u 和υ 为动量，上述关系保证动量守恒。上述下标是标记粒子，物理上感兴趣的是固定观测点，为此定义(P为置换)：



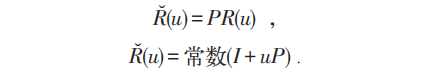
它满足：



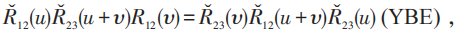
其中u，υ称为谱参数，就是杨先生文章中的kj+1-kj 。它的物理意义是三体散射的碰撞矩阵可以分解为三个两体碰撞矩阵的条件，如下图所示。



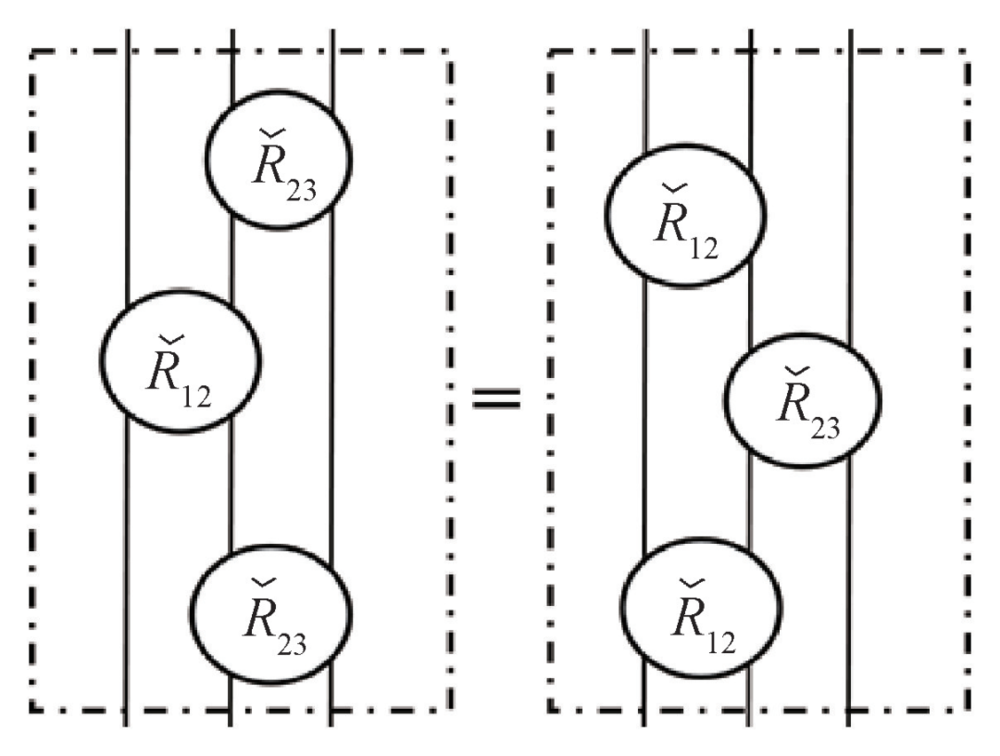
引入另外张量生成元(张量算子)Jμ，使之满足：



这就是 V. G. Drinfeld 在“Hopf Algebras and the Quantum Yang-Baxter Equation”(Soviet Math Doke，1985，32：254)中引入的代数(We should call the Yangian if α，denoted Y(α)(in honor of C. N. Yang，who found the first solution of the QYBE…)。


以上形式看起来复杂，将结构常数代入，对SU(2)， 通 常 用 I± = I1 ± iI2 ， 表 面 上 [ Jμ，Iν ]， [ Iσ , Jτ]  项有21个关系，但不独立。直接计算可证明Y(SU(2))的独立关系只有



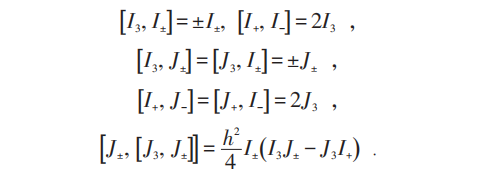
其中常数h与YBE有理解所含的参数有关。Y(SU(2))看似复杂，其实我们在物理中早就碰到过了。周知氢原子存在角动量算符L和Lunge—Lenz向量A，它们的矢积就满足Yangian关系。对SU(3)，Drinfeld关系式也可以简化，代入结构常数后，含[[Jμ，Jλ]，···]经复杂计算证明74项中有7项独立，公式不再列出了。


Yangian以后有大的发展，例如近几年E. Witten及其合作者证明与量子场论中反常有关，量子代数更引起了极大数目的研究成果。我们强调的是，Yangian不仅对近邻相互作用非线性模型适用，例如Hubbard的链模型具有Yangian不变性。长程互作用的Calogero—Sutherland模型：



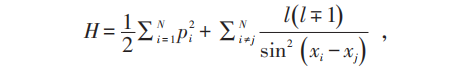
也具有Yangian对称性(详见葛墨林和薛康著《杨—巴克斯特方程》《量子力学中的杨—巴克斯特方程》)。


在辫子群相关领域，已有许多重要工作，包括Jones，Kauffman，Wadati，Witten等一系列重要的工作。


如何把杨—Mills与杨—Baxter有机结合起来，是值得关注的方向。


E. Witten同他的合作者将YM类型非阿贝尔规范量子场论与杨—Baxter结合，包括算符乘积展开、结构反常等，推广称为“动力杨—Baxter方程”（K. Costello，E. Witten，M. Yamazaki.“Guage Theory and Integrability” )。


4. 统计物理难题


统计物理难题包括了伊辛(Ising)模型(二维格点)自发磁化严格解，超导磁通量量子化，冷原子(玻色—爱因斯坦凝聚BEC)，非对角长程有序(ODLRO)，单位圆定理，相变等等。着重介绍以下三部分。


4.1 二维格子Ising模型自发磁化的计算难题


Onsage与Kaufman将此模型的2n×2n矩阵化为2n×2n，从而计算其对角元素，但不涉及非对角元。杨先生利用极限过程将其化为n×n(D算符)矩阵本征值问题，从而严格计算了包括非对角元对自发磁化的贡献，得到1/8临界指数。这是很艰难的计算。


此问题配分函数中的重要部分是：



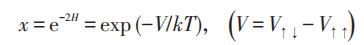
通过一系列巧妙地讨论，引入D 算子，对任意矢量ϕ 满足：



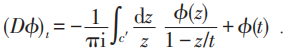
例如：




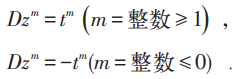
经过复杂计算，本征函数满足积分方程：



l 为本征值，所有本征值平方的连乘积决定自发磁化。其中为Jocobi椭圆函数，为双周期函数，满足：



当中J(u′，u)有I，II，III，IV种情况。在双周期矩形面积内，J 只有一个极点，在此点附近其解为：



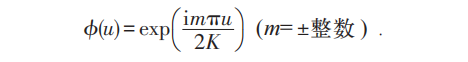
对所有本征值取连乘积，即得到自发磁化：



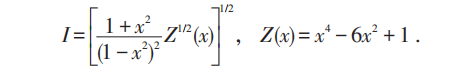
显然x=0时，I=1；时，I=0，临界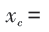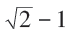，在临界点附近则有：



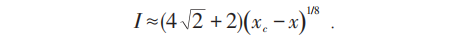
这就是著名的1/8临界指数。整个计算极为复杂困难。文章发表在Phys. Rev.，1952，85：808。


4.2 超导环中磁通量的量子化


详见杨先生文章Phys. Rev. Lett.，1961，7：46(with N. Byers)。设P区线度比渗透深度大很多，则哈密顿量为：



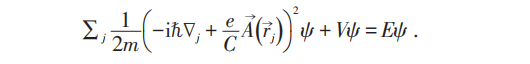
宏观考虑由于Meissner效应在P区：


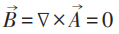
故：


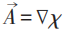
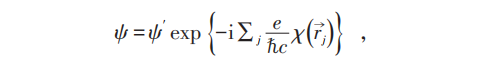
则：



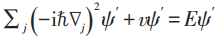
设某一电子处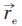，绕图中○转一圈，则ψ ′改变一常数因子，χ 为多值函数。



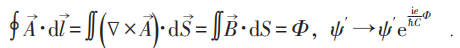
m个电子绕一圈：



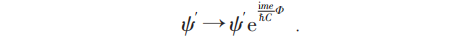
其能级对Φ 而言具周期性，且以ch/e为周期，即：



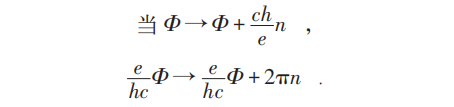
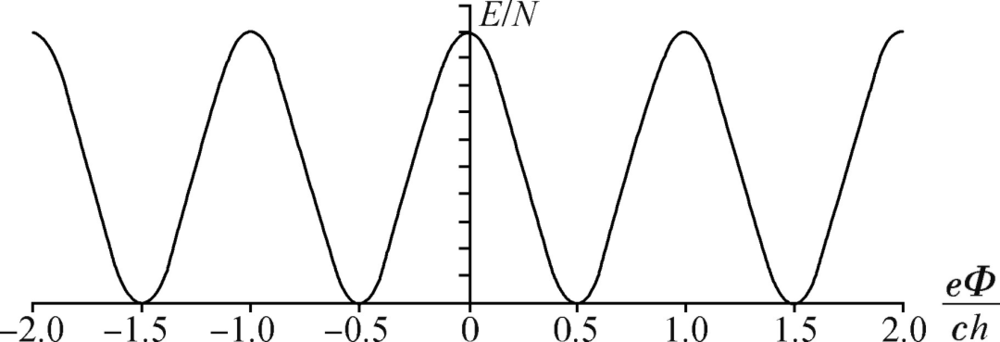
故能量E=E(Φ )是以ch/e为周期的周期函数，且为磁通量Φ 的偶函数E(Φ )=E(-Φ )。其配分函数为：



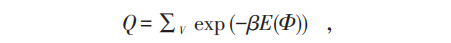
也是以ch/e为周期的偶函数。平衡态时对应自由能：


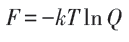
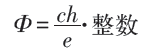
但“整数”与实验不符。


实验：



如何解决这个困难？


微观考虑：当平行于Z 轴：



动量的φ分量：



能量：



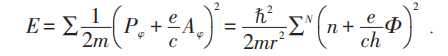
举例：当N=5时有三种可能：



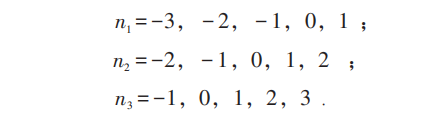
设：




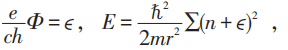
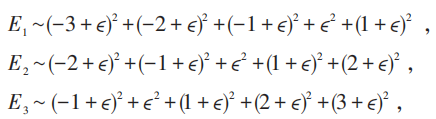
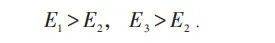
由于：



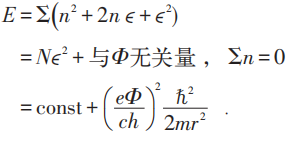
而当N=4时，使E 最低的是取n =-2，-1，0，1，


当：


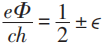
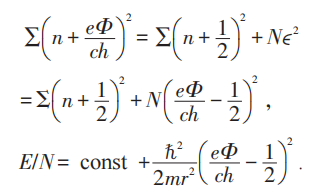
由于E (Φ )的周期性如下图所示，故N=奇数时，平衡态对应最低能态时，Φ=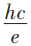·整数；故N=偶数时，平衡态对应最低能态时，Φ=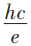·半整数。





当电子形成库珀对(Cooper pair)时，对(pair)能：



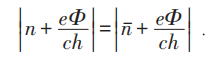
当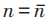时，由于不同角动量之间的库珀对无作用，不能形成凝聚，所以超导体中不允许有此情况。


另一可能：


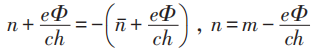
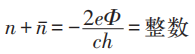
4.3 非对角长程有序(ODLRO)


刻画超导的判据：密度矩阵ρ 满足Trρ=1。ρ1表示单粒子的约化密度矩阵：



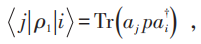
其中ai 为单粒子算符。两粒子时约化密度矩阵为：



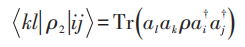
在坐标表象中，如：



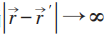
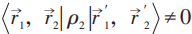
当：



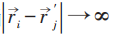
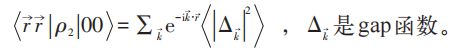
先证明其自由玻色子凝聚时导致ρ1有ODLRO。事实上由于平移不变性：



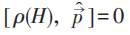
导致：



在坐标表象：



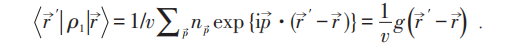
对于费米子及T>TC 时的玻色子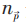，是的连续函数，当考虑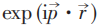急速振荡，此时：



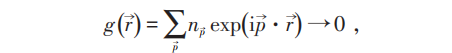
当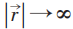时没有ODLRO！对应非凝聚态。但当T<TC，对玻色子 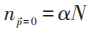( 为有理分数)，热力学极限下，即V→∞时，N/V 有限，并固定，因而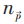：在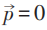处不连续，所以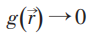的论证不成立：



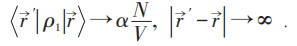
结论：玻色凝聚态⇔ρ1有ODLRO。对于费米子，ρ1没有ODLRO，但ρ2可有ODLRO。设约化密度矩阵ρ1的本征态为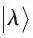，则：




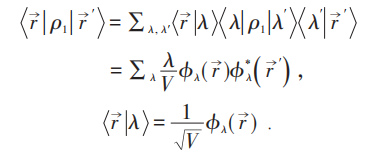
设热力学极限下：



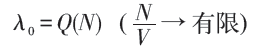
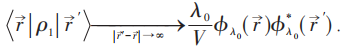
它说明当λ0比N小数量级时没有ODLRO，但ρ2可能有ODLRO。


对费米系统，其约化密度矩阵由下式给出：



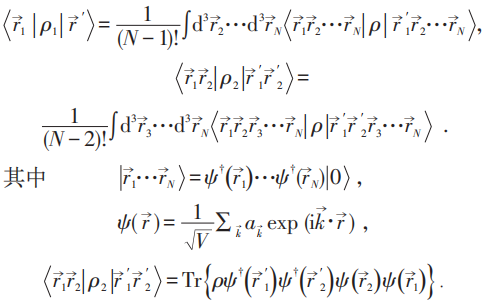
可写成：



令：


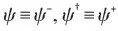
则当时，有：



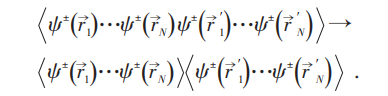
(代数)它们实际上就是关联函数。则：



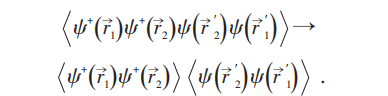
ρ2有：


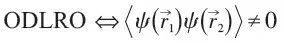
如果，则U(1)自发破坏⇔ρ2有ODLRO⇔超导相。


以下说明，ρ2有ODLRO→磁通量量子化→Meissner效应→持续流。回到均匀磁场中的电子系统：



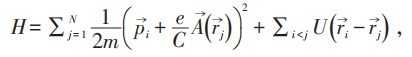
其中：




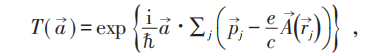
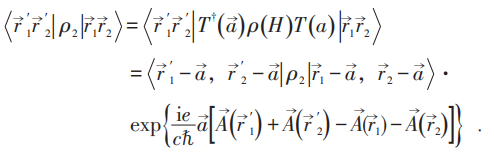
假定ρ2有ODLRO，则当时：



其中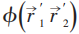是ρ2最大本征值对应的本征函数。


引入：



则：



相角：



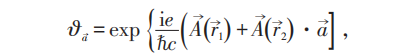
有物理意义的是：



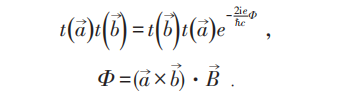
但另一方面将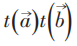作用在本征态上，可以互换，因为：



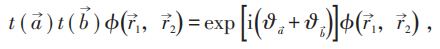
导致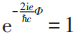，即磁通量量子化：



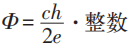
当n=0时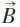，=0，就是Meissner效应(除渗透层及第二类超导体)。


超导体的面电流：



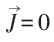
结语


综上所述，我们用尽可能简练的物理图像介绍了杨先生的物理成就，他在基本粒子角分布基础上，指出β衰变中如何测量宇称不守恒，与李政道先生获诺贝尔物理学奖。其后，把对称与破缺在基本理论中应用到极致，与李政道先生、吴大峻先生等合作，提出一系列新概念，而这一切都有实验的根据。


他提出的杨—米尔斯(YM)规范场，开创了非阿贝尔规范场新天地，在数学方面引发SDYM方程求解与几何结构的热潮，促进了物理与拓扑的联系。在物理方面，导致其后许多物理学家将SU(2)推广到SU(3)的飞跃。YM及其代数的扩大，颠覆了人们对原有局限于电磁场(U(1)规范场)的认知，扩大到非阿贝尔规范场这一完全不同的新的互作用类型，引发了标准模型、渐近自由、非阿贝尔场的重整化、动力学QCD等等，使基本粒子理论发生了革命性变化。


他提出了杨—Baxter方程，其后被扩展成数学物理的巨大领域，形成用Bethe Ansatz求解非线性可积模型的基础。它引发了孤子量子化理论，导致旋量(spinor)被预言并观测到。在数学方面促进了辫子群、量子群(包括Yangian)的出现。


他有关Ising模型严格结果、超导磁通量量子化、ODLRO、单位圆定理、相变理论、BEC的重要结果，η-pair(与张守晟合作，在Hubbard模型中发现SO(4)对称性，自然就有Yangian对称性)，还有涉及统计物理、凝聚态物理等方向的重要成果。所有以上列出的和没有列出的，都是物理的宝贵财富！


在感叹之余，深感自己水平能力之不足，理解之不深。谨以此敬祝杨振宁先生百年华诞，尽心致意。


本文选自《物理》2021年第9期，首发于微信公众号：中国物理学会期刊网（ID：cpsjournals），作者：葛墨林（南开大学陈省身数学研究所）