本文来自微信公众号:中科院物理所(ID:cas-iop),作者:Marianne,翻译:C&C,审校:zhenni,题图来自:pixabay
质数是那些只能被自身和1整除的整数,比如前七个质数是2,3,5,7,11,13,17。
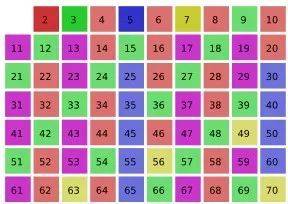
每一个正整数都可以借助一种特定的数学结构写成质数的乘积,例如 30 = 2×3×5 。质数就像是构成其他整数的基本积木,而这就是人们觉得它们有趣的原因。
质数是无穷多的,而这一点早已被古希腊数学家熟知,无论你在数轴上移动多远总有一个质数在你前面。下面是希腊最著名的数学家欧几里得的证明。
假设质数是有限的。我们可以用 p1 , p2 , p3 等来表示,直到最后一个质数 pn 。现在定义某个数字 P:

比方说如果只有5个质数:p1 = 2, p2 = 3, p3 = 5, p4 = 7, p5 = 11,那么存在一个数 P :

如果 P 本身是质数(就像在我们的例子中一样),那么很明显它不可能是我们列表中的一个质数:因为它比所有的质数都大。
如果 P 不是质数,那么,就像其他自然数一样,它一定可以写成质数的乘积。我们选一个能被 P 整除的质数,用 p 表示。可以看出, p 不能是 p1 到 pn 的任何质数,否则就会出现余数 1 :
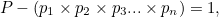
而 1 不能被任何其他的自然数整除。因此,集合 p1,p2,p3…pn 并不能包含我们假设的所有质数。这个矛盾意味着质数一定是无限多的。
几千年来,我们一直知道有无限多个质数(参见这里的证明),但并没有一个简单的公式告诉我们它们都是多少。强大的计算机算法使我们能够找到越来越大的质数,但却永远不可能把它们全部写下来。
质数定理告诉我们质数在其他整数中的分布。它试图回答这样一个问题:“给定一个正整数 n ,包括 n 在内的所有整数,有多少个是质数?”
质数定理并没有精确地回答这个问题,而是给出了一个近似值。宽泛地说,对于比较大的整数,表达式:

这是一个很准确的质数估计,而且随着n的增大,这个估计也会变得更准确。其中 ln(n) 是自然对数,可以通过计算器得到。
举个例子,让我们来看看 n=1000 的情况。此时所有质数可以在这个列表中查找。我们的估计是:

这是一个很准确的近似。
然而,要精确地理解质数定理告诉我们的东西,我们需要说出我们所说的“一个准确的近似”是什么意思。质数定理并不是说,对于一个给定的整数n,真值和我们的近似值之间的差值接近 0 。相反,它告诉我们关于“近似值占真值的百分比是多少?”的问题。
回到我们 n=1000 的例子,真值是 168,近似值是 145 。因此,近似构成的比例:
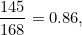
近似值占真实值的 86% ,不错。
当 n=100000 时,包含 100000 的质数是 9592 ,这是真值,估值是 8686 。
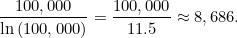
在这种情况下,估值占真值的 90% 。
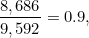
这相比于 n=1000 的情况,比例从 86% 提升到了 90% 。
一般来说,质数定理告诉我们,对于 n 很大的情况, n/ln(n) 得到的近似值几乎是真值的 100% 。事实上,你可以让它接近 100% ——只要你选择足够大的 n 。
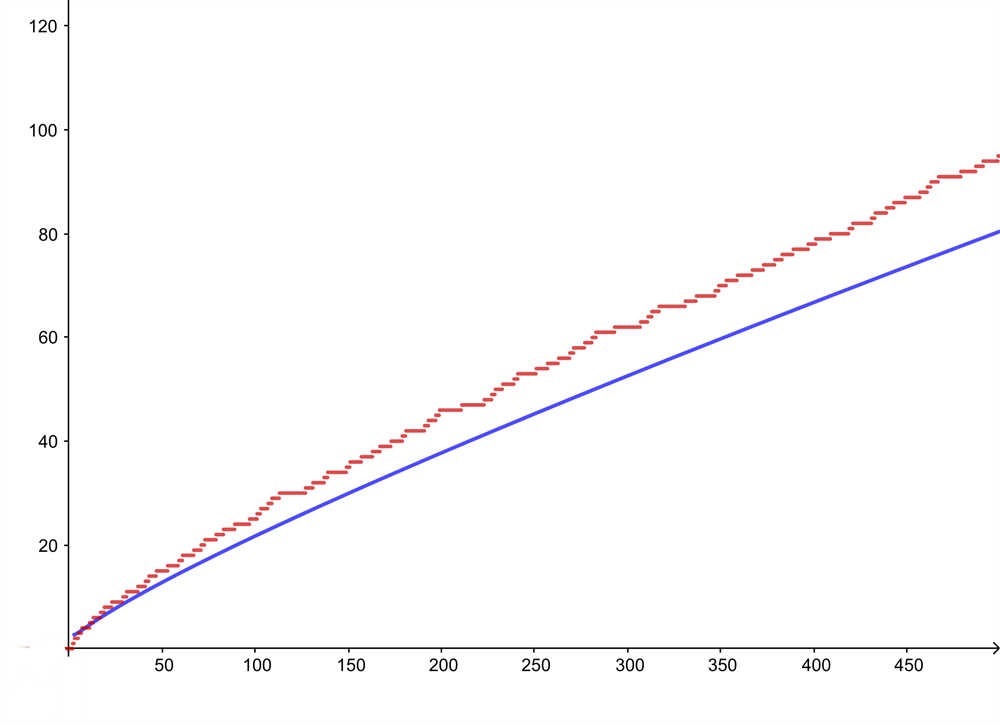
红色曲线显示的是小于或等于n的质数数目,其中横轴表示 n 。蓝色曲线给出 n/ln(n) 的值。真实结果和近似结果之间的差值随着 n 的增长而增加,但两者之间的比值趋于 1 。
为了用数学符号来描述素数定理在数学上的辉煌,让我们先用表示小于或等于的质数的数目。这个定理可以用公式表述:
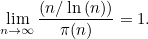
如果你懂一点微积分你就会知道你可以交换分子和分母,此时表达式 (1) 等于:

素数定理通常用第二个表达式 (2) 来表述,有时也写成:

表示:“当 n 趋近于无穷大时, n/log(n) 趋近于 π(n) ”。
原文链接:
https://plus.maths.org/content/maths-minute-prime-number-theorem
https://plus.maths.org/content/maths-minute-how-many-primes
本文来自微信公众号:中科院物理所(ID:cas-iop),作者:Marianne

