这本书的作者是德国网红数学家霍格尔·丹贝克,他在书中放了100道经典烧脑谜题和各种脑洞大开的逻辑题目,涵盖了生活段子、数字难题等多种题材,来试试自己能破解几道问题。
以下谜题与问题来自《三个逻辑学家去酒吧》,内容有删减:俄罗斯轮盘赌这道关于俄罗斯轮盘赌的题就令人毛骨悚然了。这是一个可能会致死的赌博游戏,它经常出现在电影中。
这个游戏需要一把左轮手枪,手枪上的转轮通常可以放进6颗子弹。赌徒转动转轮,在不知道转轮会在哪个位置停下的情况下,举起左轮手枪对准头部,扣动扳机。

我当然不是让你玩这个游戏,而是要做一个思想实验。你设想一下,你落入了一个可恶的罪犯头目手中。
他给你看了他的左轮手枪的转轮。你看到里面不是仅有1颗子弹,而是有2颗相邻的子弹,转轮里的另外4个弹仓是空的。

这个可恶的歹徒头领转动了转轮,然后对准一盏灯扣下了扳机。不过什么都没有发生,没有子弹射出来。
接着,他将手枪对准你并问道:「我是该马上扣动扳机呢,还是你更想要我再转动几圈转轮再开枪呢?」

提问
你会如何回答?哪种情况下你活下来的概率更大?

答案
不要将转轮再一次转动更好。
我们要计算的是枪管后有一颗子弹的概率。可以先从较简单的第二种情况开始:歹徒头目在第二次扣下扳机之前又转了一次转轮,那么,被射击中的概率就是三分之一,因为6个弹仓里有2颗子弹。
如果在第二次开枪之前没有转动转轮,那就是另外一种计算方式。因为第一枪没有子弹射出,那么在第一次开枪前,枪管后面的是4个空弹仓中的一个。在左图中,这些空弹仓被涂成了黑色。
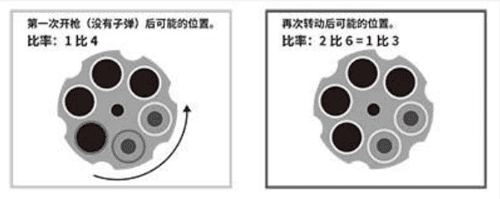
开枪之后,转轮转动了六分之一圈。我们假设,转轮向逆时针方向转动。不过也可以顺时针方向转动,最后的结果并不会因此而改变。会发生什么呢?
4个需要考虑到的弹仓用浅色圆圈表示出来了(左图)。4个弹仓中的3个相继为空弹仓,不过还有一个弹仓里有一颗子弹。也就是说,左图射出一颗子弹的概率是四分之一,而另一种情况(右图)的概率是三分之一。
因此,对歹徒头目说出的正确回答是:
他应该立刻再开一枪。因为接下来是空弹仓的可能性更大。

在自相残杀中存活下面这个问题是另一种题型,这道题有关生死。
快到午夜之时,五个黑色的身影聚集在一个黑暗的地方。这些暴徒彼此不和很多年了,现在他们想要决一死战。
他们彼此间的距离并不相同,每个人的左轮手枪里都有一发子弹能正好打中离他最近的那个人。午夜来临,当教堂的钟声响起时,这五个男人扣下了扳机……

提问请证明,至少有一个暴徒活下来了。

答案
只有一个暴徒活下来了,为什么?
由于这五个男人之间的距离是不同的,那么一定有两个暴徒之间的距离最近。因此,这两位男士会以彼此为目标,互相开枪射击对方。

那剩下的三个暴徒会做什么呢?我们需要区分两种情况:
1) 三个暴徒中的一个人会以两个互相射击的人中的某一个为目标,因为这个人离他最近。那么就会有一个人身中两枪。又因为只有五发子弹,所以至少有一个暴徒活下来了。

2) 剩下的三个人是彼此离得最近的人,那两个彼此离得最近的暴徒离他们都较远。那么在这三个人之中又会有两人的距离是最近的,这两人就会以彼此为目标相互开枪致死。
这样就没有人射击第三个暴徒了。
他活了下来。

跑步穿越沙漠骄阳无情地炙烤着,没有任何阴凉之处。只要是在炎热的沙漠里艰难地走过一次,就会知道随身携带足够多的水是多么重要。
这道题里的主人公也知道这一点。
一个运动员想用六天跑步横穿沙漠。在起点处有足够多的水和食物,但他只能携带四日份的口粮。

提问
他该如何安排才能成功穿越沙漠?
提示:
运动员起跑后,带有四日份的口粮。一天之后,只剩三份,因为有一份已经被他吃喝用尽。他还可以将口粮储存在沙漠中。

答案
横穿沙漠确实有可能,但要按如下步骤操作:
第一步:运动员带着四日份的口粮开跑。他跑完一天的路程后,在此地放置两份口粮,返身跑回起点。他在启程的路上消耗掉了一份口粮,回来的路上消耗掉了另一份口粮。
第二步:他再次携带四日份口粮开跑。一天之后,他还剩三份口粮,取出之前放置在此地的两份口粮中的一份,放进背包。带上这四份口粮,他又继续跑了一天,此时他还剩三份口粮,将其中的两份放置在沙漠里,他开始往回跑。一天之后,他从背包里拿出最后一份口粮吃喝掉,这时他到达了第一次放置口粮的地方,这里还有一日份的口粮,于是他成功回到出发点。

第三步:此人再一次带着四日份口粮出发。两天之后,他到达了存有两日份口粮的地方。他背包里原本有的四份口粮中的两份此时已经被消耗掉了,因此他可以从储存地取出两份口粮随身带上。
此时,他随身携带四份口粮,可以支撑他完成剩下的四天路程。

谁是小偷?如果我们所有人都只讲真话,我们的生活会更简单吧?
心理学家则对此有所怀疑。他们认为,谎言起着社会黏合剂的作用。老实说,谁想要总是四处听到没有修饰过的真话?
人们当然会更喜爱恭维性以及哄骗性的赞扬。还有,在逻辑爱好者的眼里,谎言也是造福社会的,因为它们是许多有趣的谜题的重要组成部分。

下面这道题也是:
博物馆里一幅珍贵的画被盗了。从监控摄像里隐约地看到有一个人,很明显这个小偷是独自作案。
警察抓住了四个男人并进行讯问。只有一个人说了真话,另外三个人都说了谎话。这里有供词:A:我没有偷画。
B:A在说谎!
C:B在说谎!
D:画是B偷的。

提问
请你找出,是哪三个人在说谎。还有,你能从中知晓是谁偷了画吗?
答案
B是唯一说真话的人,A就是要找的小偷。
解答这样的逻辑谜题,就可以用到真值表了。这个表格囊括了所有可以想到的不同情况。
列出表格后,我们来检验每种情况是否牢靠,也就是有没有矛盾。关于如何运用真值表,我们最好用具体例子来解释。四个嫌疑人中,只有一个人说了真话。我们必须区分四种不同的情况:
情况1
情况2情况3情况4A
真话
说谎者
说谎者说谎者B
说谎者真话说谎者说谎者C说谎者说谎者真话说谎者D
说谎者说谎者说谎者真话
每一列都是一种情况。
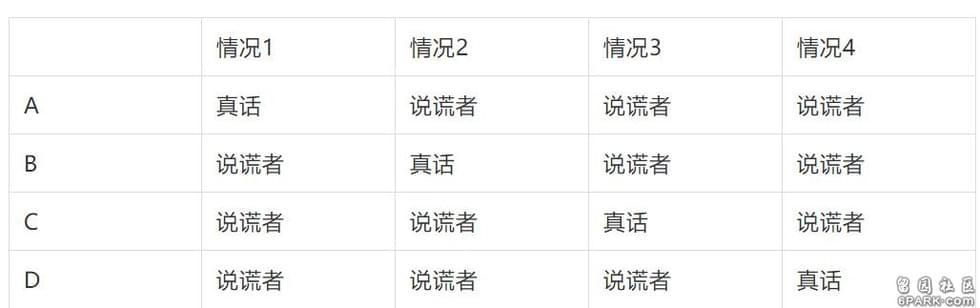
我们现在来检验,这四种情况中的哪一种没有矛盾。不过,也有可能存在多个情况都没有矛盾,那么这道题就没有明确的答案了。
这里重复一下这四句供词:
A:我没有偷画。
B:A在说谎!
C:B在说谎!
D:画是B偷的。
情况1:这种情况排除。这里面B和C两人都是说谎者。但是C说,B在说谎。若这句供词是真话,那C就不再是说谎者,这就矛盾了。
情况2:因为A说谎了,那么A就是小偷。另外三个嫌疑人的供词也并不矛盾。也就是说,只有B说了真话。
情况3:不可能。A和B两人都是说谎者。但是B说,A在说谎,那这句供词就变成了真话,不再是谎言了。这是不可解的矛盾。
情况4:这种情况我们也可以剔除。与情况3一样,如果A和B两人都是说谎者,B的供词就会存在不可解的矛盾。
足球协会的问卷调查多么奇怪的一个村庄!这里的每个村民要么是说谎者,要么是只说真话的人。
除此之外,每个村民都是四个足球协会A,B,C,D中的一个的支持者。一所民意调查机构询问了这个村庄所有250个居民以下四个问题:
1)您是A队的支持者吗?
2)您是B队的支持者吗?
3)您是C队的支持者吗?
4)您是D队的支持者吗?
有90个人对第一个问题回答了「是」,100个人对第二个问题回答了「是」,第三和第四个问题都各有80个肯定的回答。
提问请问,有多少个说谎者生活在这个村庄?回答
250个村民中有50个说谎者和200个只说真话的人。
为了找出答案,我们需要知道说谎者和说真话的人会如何回答这四个问题:
1)您是A队的支持者吗?
2)您是B队的支持者吗?
3)您是C队的支持者吗?
4)您是D队的支持者吗?
每个说真话的人,会对其中一个问题回答「是的」(因为他支持四队中的一队),对其他三个问题回答「不是」。
而说谎者恰好相反,只会回答一次「不是」(问到他支持的球队时),回答三次「是的」(问到他不支持的那些球队时)。
我们总结一下:每个说真话的人会给出一次肯定的回答,每个说谎者会给出三次肯定的回答。
由此,我们设w是说真话者的数量,l是说谎者的数量,那么所有肯定回答的总数量就是w+3l。
而肯定回答的总数量很简单就能计算出来:
1)您是A队的支持者吗?90个肯定回答。
2)您是B队的支持者吗?100个肯定回答。
3)您是C队的支持者吗?80个肯定回答。
4)您是D队的支持者吗?80个肯定回答。
肯定回答的数量是90+100+80+80=350。
另外,因为村庄里有250个居民,我们得知w+l=250。由此可以得出以下方程组:w+l=250w+3l=350由此可得:2l=100,即l=50。因此,有50个说谎者。