本文来自微信公众号:科学大院(ID:kexuedayuan),作者:望墨溢(单位:西北工业大学航海学院),头图来自:《命运之夜UBW》
当你点进来的时候,首先得确认一件事:你得有老婆(当然女朋友也行)。
为什么呢?因为本篇推送是作者基于坚实的数学基础和丰富的生活体验写出来的。为充分反驳“学数学没啥用”的谬论,这次,作者就用一组经典案例,介绍概率学在了解老婆情绪变化中的应用。

随机事件与随机变量
某些事情的发生或现象的出现,在概率学中被称为事件(Event)。有些事件的发生具有随机性,即事前不知道该事件是否发生,或者事件的走向尚未明晰,这种具有随机性的事件被称为随机事件(Random Event)。
例如,“老婆生气”是一个随机事件,“老婆不生气”也是一个随机事件;或者,“老婆喜欢这款包包”是一个随机事件,“老婆喜欢那款包包”也是一个随机事件。
为了用数学描述随机事件,数学家引入随机变量(Random Variable)的概念,指取值具有随机性的变量。例如,“老婆情绪”是个随机变量,可以等于“生气”,也可以等于“不生气”,具体取值是随机的。
此外,“生气”和“不生气”组成了“老婆情绪”这个随机变量的样本空间(Sample Space),“生气”和“不生气”称为该样本空间的样本点(Sample Points)。

大数定律与古典概率
最初,人们没有概率的概念,只有频率(Frequency)的概念,即在相同的条件下,多次试验中某事件发生的次数。例如,在你表现良好的条件下,统计1000次老婆的情绪,老婆生气了200次,即老婆生气的频率是20%,不生气的频率是80%。
而根据伯努利大数定律(Bernoulli's Law of Large Numbers),只要统计的次数足够多,频率将无限接近概率。注意,统计必须满足“相同条件”,若有其它因素干扰(例如,你时不时惹她生气),则统计结果将失去意义。

最初的概率模型是古典概率(Classical Probability),又称等可能概率。古典概率认为,样本空间中样本点数有限,且概率相等。若某一事件包含多个样本点,则该事件的概率与包含的样本点数成正比。
例如,老婆既喜欢吃串串,也喜欢买包包,且认为对每一种串串和每一款包包的喜好程度是一样的。每一种串串和每一款包包,共同组成“老婆喜好”这个随机变量的样本空间。
显然,事件“给老婆买串串”={串串1,串串2,…,串串n},事件“给老婆买包包”={包包1,包包2,…,包包N}。由于串串的种类n小,而包包的款型N大(备注1:虽然不明白有什么区别,但明白的是,她手上永远缺一只包包),那么,“给老婆买包包”的正确概率就是:
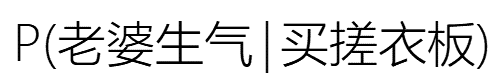
而“给老婆买串串”的正确概率就是:
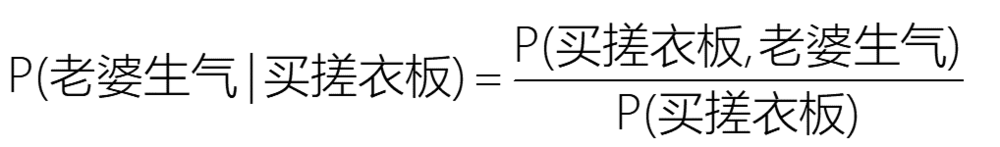
明显,P(给老婆买包包)>P(给老婆买串串)。

概率分布与中心极限定律
可后来人们发现,实际中样本点的概率往往是不同的。例如,相比500元的包包,老婆更喜欢2000元的包包。设随机变量“包包”表示老婆喜欢的包包款式,那么P(包包=2000元的包包1)>P(包包=500元的包包2)。
为此,人们引入概率分布(Probability Distribution)的概念,即随机变量不同取值(样本点)的概率不同。下文中,概率表示事件的概率,概率分布表示随机变量的概率函数。
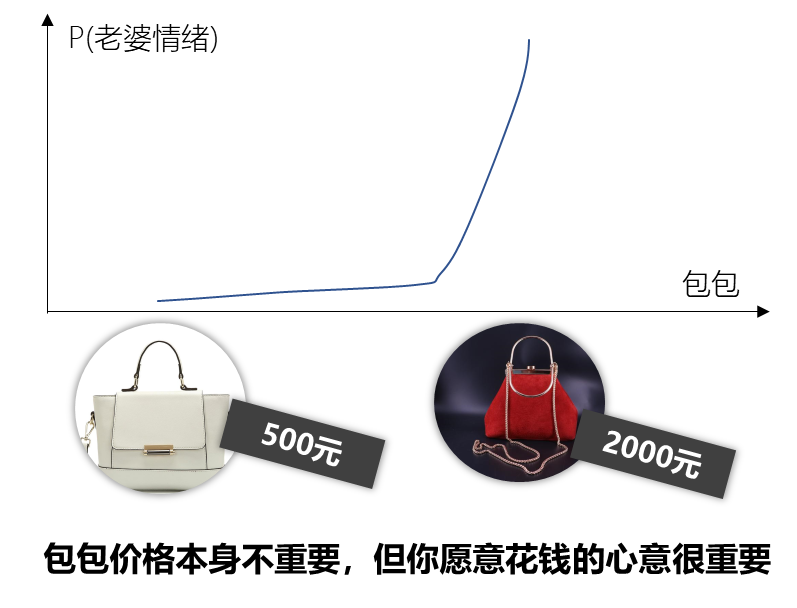
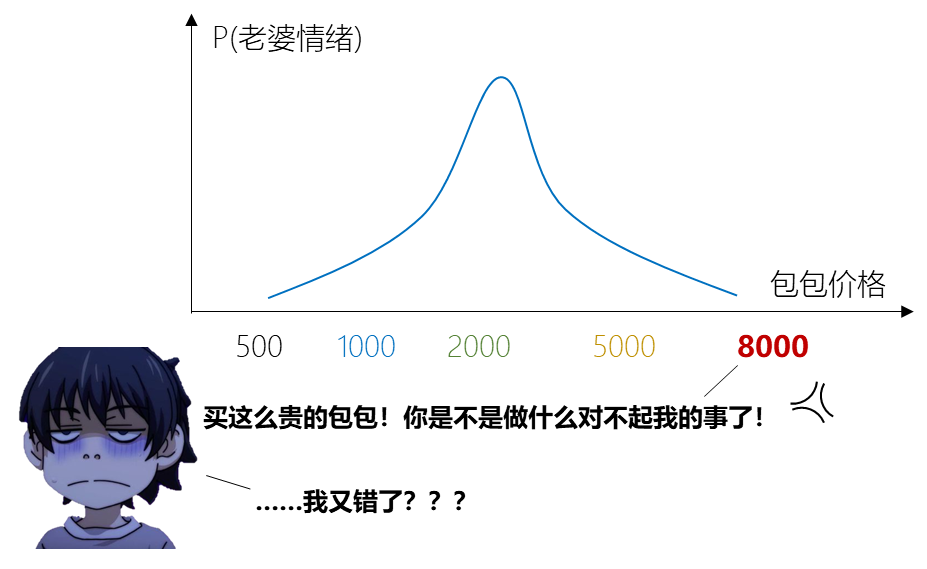
根据中心极限定律(Central Limit Law),当样本足够多时,任何随机变量的分布都将是高斯分布(Gaussian Distribution),也称正态分布(Normal Distribution)。例如,也不是包包越贵,老婆就一定越喜欢,老婆心中有一个最优价位,比这个价位高或低,“老婆的情绪”都不会最开心。(备注2:别不信,价位太高老婆会觉得你在掩饰什么!)
当然,不同人高斯分布的均值(包包的最优价位)和方差(对其他价位的接受程度)不同。均值越高(坐标右移),对包包的要求越高;方差越小(高斯分布越“瘦”),越不愿将就(和最优价位差一点,喜爱度迅速下降,你也就有危险了~)。


条件概率与全概率公式
很多时候,某个事件的发生是以另一事件为条件的。或者说,考虑一个事件发生,能够改变另一事件发生的概率。例如,很多人总以为“老婆生气”和“买搓衣板”这两件事没有关系。而实际上,“老婆生气”会导致“买搓衣板”,看到老婆“买搓衣板”你就该猜到:老婆怎么又生气了。(备注4:买搓衣板是让你跪的!难不成是她要洗衣服?)
因此,引入条件概率(Conditional Probability)的概念,指一个事件在另外一个事件发生条件下的概率。例如,老婆的生气是有预警的,当她突然买搓衣板,大概率是她生气了。看到老婆“买搓衣板”(条件),推测“老婆生气”概率就可记为:
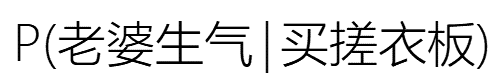
根据全概率公式(Total Probability Formula),有:
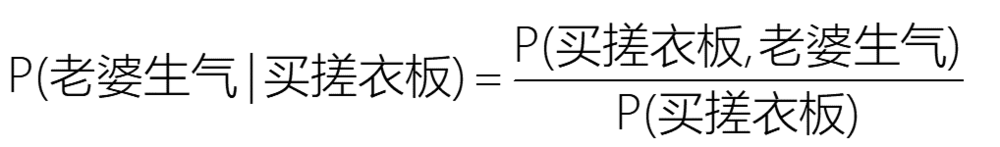
你以为“买搓衣板”和“老婆生气”同时发生是联合概率——P(买搓衣板,老婆生气)。而实际上,二者是条件概率——P(老婆生气|买搓衣板)。由于P(买搓衣板)<1,因此P(老婆生气|买搓衣板)>P(买搓衣板,老婆生气)。(备注5:新的风暴已经出现,怎么能够还看不见……)

贝叶斯公式与后验概率
若想改变老婆生气的概率,该怎么做呢?根据贝叶斯公式(Bayes Formula),有

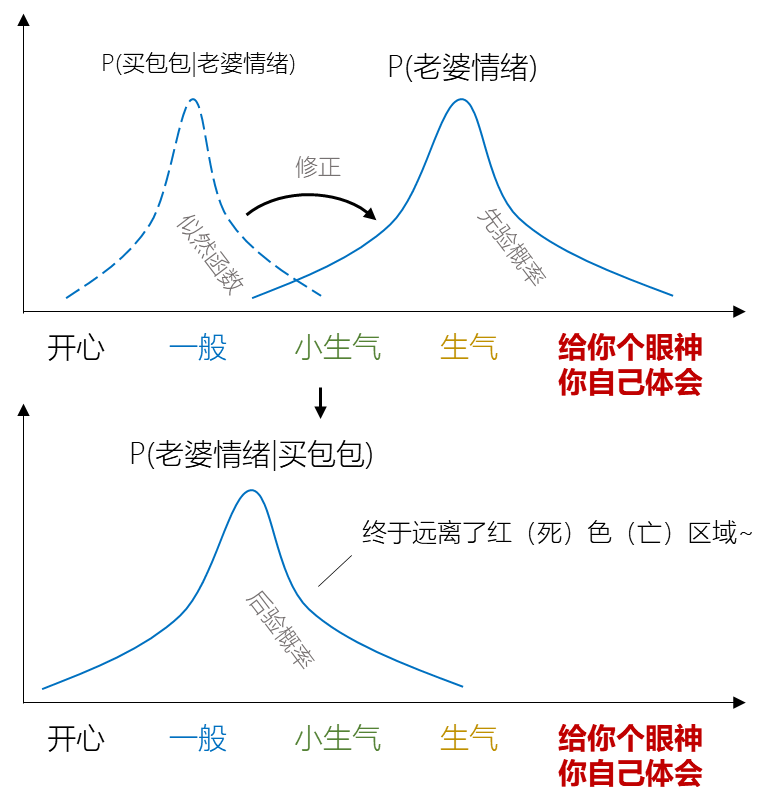
其中,P(老婆生气)为先验概率(Prior Probability),表示我们事先知道的信息,例如日常统计老婆生气的概率;P(买包包|老婆生气)为似然函数(Likelihood Function),表示某组动作和事件的接近程度或相似程度。显然,你给老婆买包包,她反而生气的似然函数很小;
P(老婆生气|买包包)为后验概率(Posterior Probability),表示我们利用“买包包”这个动作来修改“老婆生气”先验概率的结果;另外,P(买包包)可被看做归一化(Normalization)。很明显,“买包包”这个动作使得“老婆生气”的概率减小了。即P(老婆生气|买包包)<P(老婆生气)。
先验概率、似然函数往往是均值、方差不同的高斯分布,这时后验概率也是高斯分布,其均值、方差是似然函数对先验概率的修正。贝叶斯公式就是用动作(的似然函数)来修改事件的先验概率,从而得到该事件的后验概率。
贝叶斯估计准则与其它点估计
在得到贝叶斯后验概率后,可以根据两种准则来进行决策或估计,分别为后验期望(Expected A Posterior, EAP)准则和最大后验(Maximum A Posteriori, MAP)准则。
有些随机变量可以加权求和,就能使用EAP准则。例如,老婆喜欢2000元包包的概率是80%,喜欢500元包包的概率是20%。根据EAP准则,我们应买:
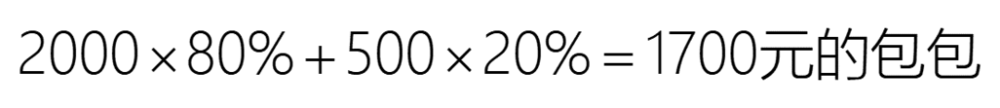
而有些随机变量不能加权求和,就只能使用MAP准则。例如,老婆喜欢狗狗的概率是80%,喜欢猫猫的概率是20%。由于世界上还没有80%狗+20%猫的物种,因此我们应买最有可能令老婆开心的狗狗!

实际中,我们不总是可以得到贝叶斯最优估计。这时,可使用其它点估计准则,例如极大似然(Maximum Likelihood, ML)估计、加权最小二乘(Weighted Least Square, WLS)估计、最小均方(Least Mean Square, LMS)估计等,但一般这些方法都是次优的。

代价函数与条件风险
实际中,不能单纯地只考虑概率分布,还应考虑不同取值带来的后果。代价函数(Cost Function)就是对随机变量不同取值后果的度量。
例如,若不给老婆买包包,虽然老婆生气的条件概率只有20%,即P(老婆生气|不给老婆买包包)=20%,但老婆生气的后果极为严重,会让你的伙食水准-10年,幸福感-100点。(备注6:老婆生气的概率再小,也不能冒这个险!)
条件风险(Conditional Risk)就是代价函数按照条件概率分布的积分,表示某个条件/行为带来的综合代价。例如,不给老婆买包包,老婆生气概率是20%,代价是幸福感-100点,老婆不生气的概率是80%,代价是幸福感+5点。那么,“不给老婆买包包”的条件风险等于:
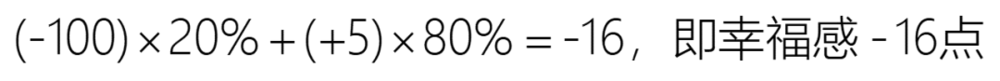
可见,不给老婆买包包,是一件风险极大的事。

总结与启示
最后,概率思维本质上是承认世界是不确定的(概率),任何事件都由一系列相互耦合、高度非线性甚至非因果的因素决定。我们永远无法消除不确定性,努力不一定成功,付出不一定收获,学习不一定成长。
但是,我们可以用努力、付出和学习等一系列动作,改变原有的概率,降低不确定性(条件概率、贝叶斯公式)。改变后的不确定性,在一次事件/尝试中无法体现,但只要持之以恒,当事件/尝试足够多时,就能够显示你和别人不同的概率分布(大数定律)。
回到题目。老婆的性格(先验概率)短期无法改变,但你的态度和行为(似然函数)可以影响她的情绪(后验概率)。所以,如果老婆生气,那一定不是老婆的问题,是因为她觉得你不在乎她!(备注7:老婆消消气,我们去买买买!)
本文图片均由作者绘制/素材加工。本文不必参考任何文献,文中有关老婆生气的场景在一般的日常生活中都能见到。若未曾碰到,请先去找个女朋友。
本文来自微信公众号:科学大院(ID:kexuedayuan),作者:望墨溢

