本文来自微信公众号：量子位（ID：QbitAI），作者：边策、杨净，原文标题：《困扰数学家25年的“切苹果”难题，被一位华人统计学博士解决了》，头图来自：IC photo
请听题：
如何将苹果平均一分为二，还能保证它长时间的新鲜？
这是一个严肃的科学问题，已经困扰了人类数学家25年之久。
根据常识，就是要保证果肉暴露在外面的面积最小，也就是切片的面积最小。如果跨越到更高的维度，是否依然成立？
这就是1995年，由三位数学家提出的一个几何学猜想。
现在，这个难题被一位华人统计学博士，解决了。
成果一经发布，就迅速引起了数学、理论计算机科学、统计学等多个领域的科学家的关注。
他们一致认为，数学大师、菲尔兹奖得主，原本猜想的提出者Jean Bourgain（让·布尔甘）一定会对这一进展感到兴奋。
毕竟，在他去世前（2018年）的几个月里还在关心这一问题进展，但终其一生都未能解决。
困扰数学家25年的几何问题
1984年，著名数学家让·布尔甘提出了一个猜想。
一个任意维度的凸体，用低一维的平面去平分，那么存在一个常数c，让凸体至少存在一个切面的面积大于c。
换句话说，如果你一刀平分“任意维度空间的西瓜”，随便你怎么劈，总有一个切面总大于c。
（Ps：以往的科学家用的是苹果的例子。但准确来说不能选苹果，因为苹果上下是凹的。）
在3维空间中，这个结论似乎很好理解，因为无论西瓜长成什么奇形怪状，总不可能在每个角度都细长。
像长西瓜，竖直切下去，切面很小，可以你也可以水平切开平分它，这样切面就会很大。
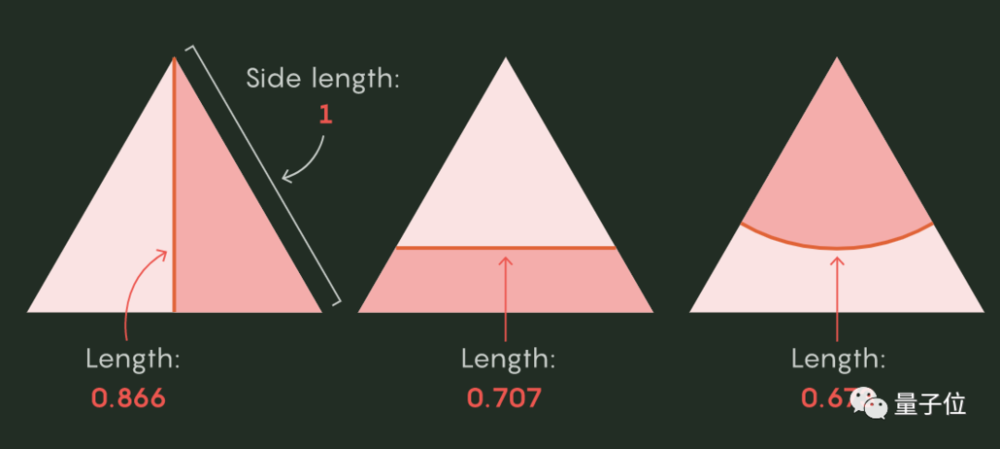
到了更高维度的空间中，二等分的最佳平面和最佳曲面差距会变大吗？切面的面积是否和维度d有关？
这个问题已经不再是纯粹的数学问题。
普林斯顿大学数学系教授Assaf Naor表示，KLS猜想在纯粹的数学和理论计算机科学中都很重要。
KLS猜想的结果，直接关系到随机行走算法的运行时间，如机器学习模型中采样问题。
所以最后解决这个几何问题的学者，都并非几何学的专家，而是来自计算机界。
用统计方法解决他
经过数学家的抽象，KLS猜想就像一个封装着气体的容器，找到最佳切面就是寻找容器的“瓶颈”。
想象一个哑铃形状的容器，里面有一个气体分子在随机运动，哑铃中间连接部分越细，分子就越难跑到另一侧。
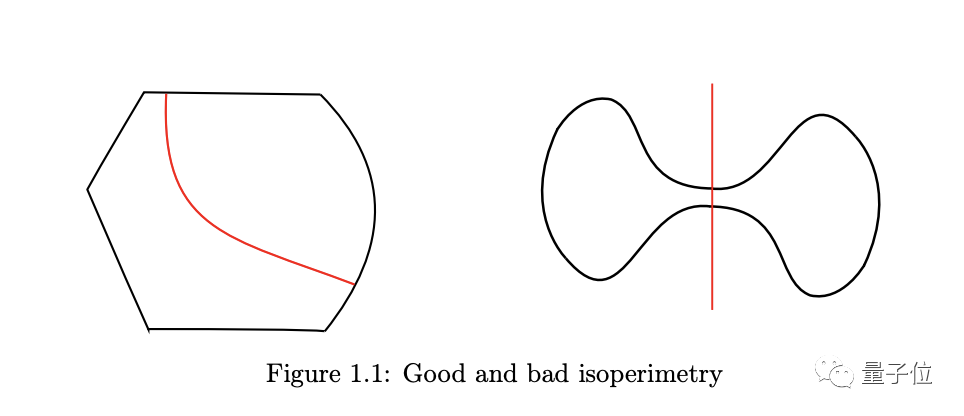△哑铃形的平分切面很小（来源：Yin Tat Lee论文）
现在人们想知道，在高维空间，这个凸的容器最细的地方有多细。（当然，哑铃并非是凸的。）
2012年，Eldan通过引入一种称为随机定位的技术，来降低这个问题与维度上界。（到底是维度d的几次幂。）
2015年末，华盛顿大学的Vempala和Yin Tat Lee改进了Eldan的随机定位，以进一步将KLS因子（用于描述瓶颈是否存在）降低到维度的四次根d1/4。
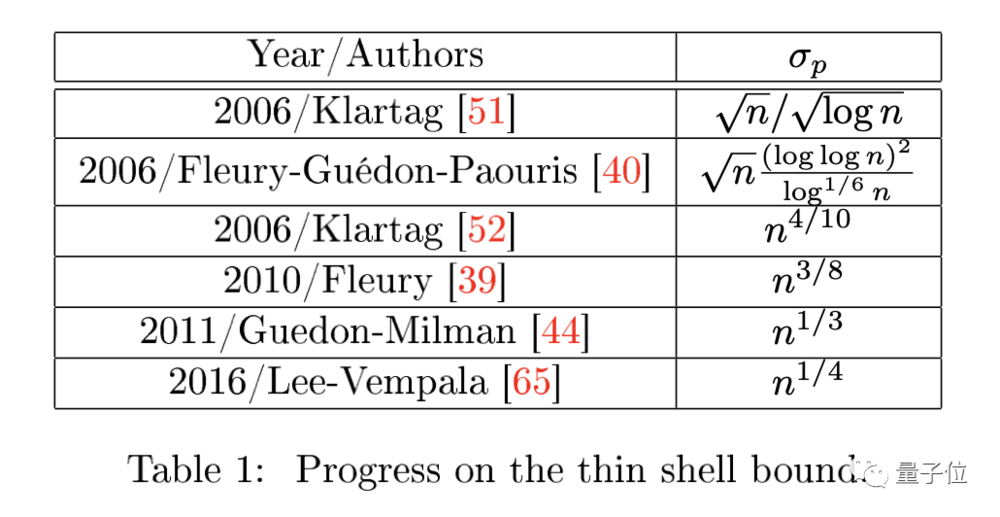
甚至，他们还将幂指数降低到几乎为0，由于d的0次幂总是等于1，Lee和Vempala似乎证明了KLS因子是一个与维度无关的常数。
他们在arXiv上发布了他们的论文。但是几天后，这篇文章就被人发现了一个缺陷，他们关于d0的证明是错的。
之后，二人修改了文章，把界限重新调整到d1/4。几年来，研究人员认为KLS猜想的探索已经到此终结了。
不过他们还在论文中，保留了d0证明的一些想法。这也为后来的突破埋下伏笔。
他们的论文引起了另一位统计学者Yuansi Chen的注意。
Chen当时是加州大学伯克利分校的统计学研究生，他正在研究随机采样方法的混合率。而随机抽样是许多类型统计推断中的关键，例如贝叶斯统计。
Chen深入研究文学，花了数周时间试图填补Lee和Vempala的证明中的空白，但依然没有解决。
于是他转变了思路，在Lee和Vempala的思想指导下，他找到了一种方法，采用递归来降低KLS因子上界。
经过反复迭代，这种方法将KLS猜想问题再次拉回到d0的上界。
这一结果意味着，高维凸形物体不会有哑铃那样的结构。
该定理的结果意味着，在n维凸体中随机行走，遍历整个图形的速度比我们之前预想得要快得多。
这将有助于计算机科学家对不同的随机采样算法进行优先级排序。
三个计算机相关的科学家
虽然表面看上去，这三位学者似乎跟数学没什么关系。
但仔细翻看他们的履历，他们都曾跟数学结下了不小的缘分。
首先，直接与研究相关的这位统计学博士后——Yuansi Chen （陈远思，音译）。
但点赞祝贺之余，也有不少学者表示十分遗憾。
因为提出这一猜想的人菲尔兹奖得主布尔甘已于2018年去世，如果他还在的话，一定会为这一进展感到兴奋。
据QuantaMagazine报道，布尔甘曾在去世前几个月，联系了他的朋友、特拉维夫大学教授Vitali Milman，询问这一猜想是否有任何进展，想在离开之前知道答案。
但Vitali Milman说，布尔甘在这一问题上，花费的时间和投入的精力比任何其他问题多得多。没想到，最后这个问题却被统计学解决了。
参考链接：
[1]https://www.quantamagazine.org/statistics-postdoc-tames-decades-old-geometry-problem-20210301/
[2]https://www.cc.gatech.edu/~vempala/papers/kls_survey.pdf
[3]https://arxiv.org/abs/2011.13661
[4]http://yintat.com/
[5]https://people.math.ethz.ch/~chenyua/
[6]https://www.cc.gatech.edu/news/604802/computer-scientists-make-kls-conjecture-breakthrough
本文来自微信公众号：量子位（ID：QbitAI），作者：边策、杨净